Rectangular Cartesian Co-ordinates

What is Rectangular Cartesian Co-ordinates?

Let O be a fixed point on the plane of this page; draw mutually perpendicular straight line XOX’ and YOY’through O.

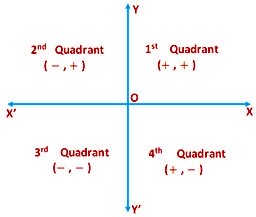
Clearly, these lines divide the plane of the page into four parts. Each of these parts is called a Quadrant; the parts XOY, YOX’, X’OX are respectively called the first, second, third and fourth quadrant. The fixed point O is called the origin and the straight lines XOX’ and YOY’ are called the co-ordinate axes; separately the line XOX’is called the x-axis and the line YOY’ is called the y-axis.

We can uniquely determine the position of any point on the plane of the page referred to co-ordinate axes drawn through O.

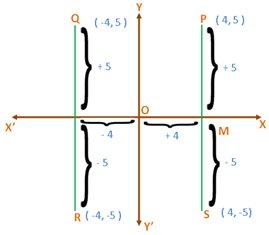
Let P be any point in the first quadrant. From P draw PM perpendicular on x-axis. If OM and MP measure 4 and 5 units respectively then the position of P on the plane is determined i.e., to get the point P on the plane, we are to move from O through a distance of 4 unite along OX and then to proceed through a distance of 5 units in direction parallel to OY. Note that, we shall have points Q, R and S in the second, third and fourth quadrants respectively and the distance of each of them along x-axis and y-axis are 4 and 5 units respectively. Therefore, it is possible to have four different point on the plane of the page at equal distances along the co-ordinate axes. To differentiate among the position of such points we introduce the following convention regarding the signs of distances along the co-ordinate axes:

(i) the distance measured from O along x-axis on the right side (i.e., in the direction OX or in direction parallel to OX is positive and the distance from O along x-axis on the left side (i.e., in the direction OX’ or in direction parallel to OX’ is negative;

(ii) the distance measured from O along y-axis in the upward direction (i.e., in the direction OY or in direction parallel to OY) is positive and the distance from y- axis in the downward direction (i.e., in the direction OY’ or in direction parallel to OY’) is negative.

By the above convention of sign the distances along x-axis as well as along y- axis are positive for P, for the point Q, the distance along x-axis is negative and that along x-axis is negative and that along y- axis is positive, for R both these distances are negative and for S the distance along x-axis is positive and that along y is negative.

From the above discussion it is evident that to determine uniquely the position of a point on a plane referred to mutually perpendicular co-ordinate axes drawn through an origin O we require two signed real numbers. These two signed real numbers together are called the rectangular Cartesian co-ordinates of the given point we write the two signed real number in braces putting a comma between them where the first number is the distance from origin along x-axis and the second number is the distance from origin along y-axis (or parallel to y-axis).

Therefore, the Cartesian co-ordinate of a point on a plane may be defined as an ordered pair of signed real numbers. Thus, the co-ordinate of the points P, Q, R and S are (4, 5), (-4, 5), (-4, -5) and (4, -5) respectively. In general , the statement, the co-ordinate of a point A are (a, b) means that the point A is situated at distance a units from origin O along x-axis and at distance b units from origin along (or parallel) to y- axis. Depending on the signs of a and b the point A may be on the first or second or third of fourth quadrant. Here, a is called the abscissa or x co-ordinate of A and b is called the ordinate or y co-ordinate of A. clearly, abscissa and ordinate are both positive for any point lying in the first quadrant; abscissa and ordinate is positive for any point lying in the second quadrant; abscissa and ordinate are both negative for any point lying in the third quadrant while the abscissa is positive and ordinate is negative for any point lying in the fourth quadrant. Conversely, if x,y are real and positive then the point.

    Having co-ordinate (x, y) lies in the first quadrant, 

    Having co-ordinate (-x, y) lies in the second quadrant, 

    Having co-ordinate (-x, -y) lies in the third quadrant, 

    Having co-ordinate (x, -y) lies in the fourth quadrant. 

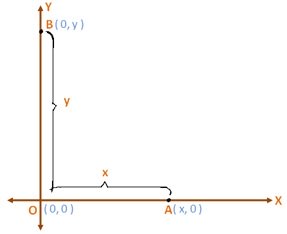
Note: That the ordinate of any point on x-axis is zero, abscissa of any point on y-axis is zero and both the abscissa and ordinate of the origin O are zero. Therefore, the co-ordinate of a point on x-axis are of the form A (x, 0), the co-ordinate of a point on y-axis are of the form B (0, y) and the co-ordinate of the origin O are always (0, 0).


The co-ordinate axes through the origin O are said to be oblique if they are not inclined at right angles. The co-ordinate of a point on a plane referred to oblique axes are called oblique co-ordinate. The present treatise deals mainly with rectangular co-ordinates.

Examples on Quadrant:

In which quadrant do the following points lie?

(i) (4, -6)

Solution:

For the point (4, -6) we see that the abscissa = 4, is positive and ordinate = -6, is negative.

Therefore, the point (4, -6) lies in the fourth quadrant.


(ii) (2, 3)

Solution:

For the point (2, 3) we see that the abscissa and ordinate are both positive.

Hence, the point (2, 3) lies in the first quadrant.


(iii) (-2, 1 - √3)

Solution:

Since - √3 > 1, hence (1 - √3) is negative. Hence, the abscissa and ordinate are both negative for the point (-2, 1 - √3).

Therefore, the point (-2, 1 - √3) lies in the third quadrant.


(iv) (√3 - 2, 5)

Solution:

Since, √3 < 2, hence (√3 - 2) is negative. Thus abscissa is negative and ordinate is positive for the point (√3 - 2, 5).

Therefore, the point (√3 - 2, 5) lies in the second quadrant.

● Co-ordinate Geometry 

• What is Co-ordinate Geometry?
  
• Rectangular Cartesian Co-ordinates
  
• Polar Co-ordinates
  
• Relation between Cartesian and Polar Co-Ordinates
  
• Distance between Two given Points
  
• Distance between Two Points in Polar Co-ordinates
  
• Division of Line Segment: Internal & External
  
• Area of the Triangle Formed by Three co-ordinate Points
  
• Condition of Collinearity of Three Points
  
• Medians of a Triangle are Concurrent
  
• Apollonius' Theorem
  
• Quadrilateral form a Parallelogram 
  
• Problems on Distance Between Two Points 
  
• Area of a Triangle Given 3 Points
  
• Worksheet on Quadrants
  
• Worksheet on Rectangular – Polar Conversion
  
• Worksheet on Line-Segment Joining the Points
  
• Worksheet on Distance Between Two Points
  
• Worksheet on Distance Between the Polar Co-ordinates
  
• Worksheet on Finding Mid-Point
  
• Worksheet on Division of Line-Segment
  
• Worksheet on Centroid of a Triangle
  
• Worksheet on Area of Co-ordinate Triangle
  
• Worksheet on Collinear Triangle
  
• Worksheet on Area of Polygon
  
• Worksheet on Cartesian Triangle

11 and 12 Grade Math 

From Rectangular Cartesian Co-ordinates to HOME PAGE