Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Medians of a Triangle are Concurrent
Proof the medians of a triangle are concurrent using co-ordinate geometry.
To proof this theorem we need to use the formula of co-ordinates of the point dividing the line segment joining two given points in a given ratio and the mid-point formula.
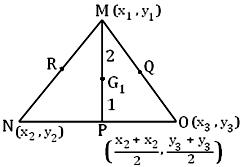
Let (x₁, y₁), (x₂, y₂) and (x₃, y₃) be the rectangular cartesian co-ordinates of the vertices M, N and O respectively of the triangle MNO. If P, Q and R be the mid-points of the sides NO, OM and MN respectively, then the co-ordinates of P, Q and R are ((x₂ + x₃)/2, (y₂ + y₃)/2)) , ((x₃ + x₁)/2 , (y₁ + y₂)/2)) respectively.
Now, we take a point G₁ on the median MP such that MG₁, G₁P = 2 : 1. Then the co-ordinates of G₁ are
= ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)
Again, we take a point G₂ on the median NQ such that NG₂ : G₂Q = 2 : 1. Then the co-ordinates of G₂ are
= ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)
Finally, we take a point G₃ on the median OR such that OG₃ : G₃R = 2 : 1. Then the co-ordinates of G₃ are
= {(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3}
Thus we see that G₁, G₂ and G₃ are the same point. Hence, the medians of the triangle are concurrent and at the point of concurrence the medians are divided in the ratio 2 : 1.
Note:
The point of concurrence of the medians of the triangle MNO is called its centroid and the co-ordinates of the centroid are {(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3}
Worked-out examples on medians of a triangle are concurrent:
1. If the Co-ordinates of the three verticals of a triangle are (-2, 5), (-4, -3) and (6, -2), find the Co-ordinates of the centroid of the triangle.
Solution:
The Co-ordinates of the centroid of the triangle formed by the joining the given points are {(- 2 - 4 + 6)/3}, (5 - 3 - 2)/3)}
[Using the formula {(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3}]
= (0, 0).
2. The co-ordinates of the vertices A, B, C of the triangle ABC are (7, -3), (x, 8) and (4, y) respectively; if the co-ordinates of the centroid of the triangle be (2, -1), find x and y.
Solution:
Clearly, the co-ordinates of the centroid of the triangle ABC are
{(7 + x + 4)/3, (- 3 + 8 + y)/3)} = {(11 + x)/3, (5 + y)/3}.
By problem, (11 + x)/3 = 2
or, 11 + x = 6
or x = -5
And (5 + y)/3 = -1
or, (5 + y) = -3
or, y = -8.
Therefore, x = -5 and y = -8
3. The co-ordinates of the vertex A of the triangle ABC are (7, -4). If the co-ordinates of the centroid of the triangle be (1, 2), find the co-ordinates of the mid-point of the side BC.
Solution:
Let G (1, 2) be the centroid of the triangle ABC and D (h, k) be the mid-point of the side BC.
Since G (1, 2) divides the median AD internally in the ratio 2 : 1, hence we must have,
(2 ∙ h + 1 ∙ 7)/(2 + 1) = 1
or, 2h + 7 = 3
or, 2h = -4
or, h = -2
And {2 ∙ k + 1 ∙ (-4)}/(2 + 1) = 2
or, 2k - 4 = 6
or, 2k = 10
or, k = 5.
Therefore, the co-ordinates of the mid-point of the side BC are (-2, 5).
● Co-ordinate Geometry
- What is Co-ordinate Geometry?
- Rectangular Cartesian Co-ordinates
- Polar Co-ordinates
- Relation between Cartesian and Polar Co-Ordinates
- Distance between Two given Points
- Distance between Two Points in Polar Co-ordinates
- Division of Line Segment: Internal & External
- Area of the Triangle Formed by Three co-ordinate Points
- Condition of Collinearity of Three Points
- Medians of a Triangle are Concurrent
- Apollonius' Theorem
- Quadrilateral form a Parallelogram
- Problems on Distance Between Two Points
- Area of a Triangle Given 3 Points
- Worksheet on Quadrants
- Worksheet on Rectangular – Polar Conversion
- Worksheet on Line-Segment Joining the Points
- Worksheet on Distance Between Two Points
- Worksheet on Distance Between the Polar Co-ordinates
- Worksheet on Finding Mid-Point
- Worksheet on Division of Line-Segment
- Worksheet on Centroid of a Triangle
- Worksheet on Area of Co-ordinate Triangle
- Worksheet on Collinear Triangle
- Worksheet on Area of Polygon
- Worksheet on Cartesian Triangle
From Medians of a Triangle are Concurrent to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
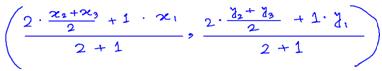
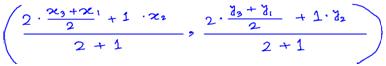
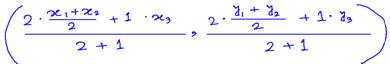


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.