Subscribe to our YouTube channel for the latest videos, updates, and tips.
Properties of Factors
The properties of factors are discussed step by step according to its property.
Property (1):
Every whole number is the product of 1 and itself so
(i) Each number is a factor of itself.
19 x 1 = 19,
So, 19 is the factor of 19.
(ii) 1 is the factor of every number.
We know that a number multiplied by 1 is the number itself. So, 1 is a factor of every number.
For example
21 ÷ 1 = 21. So, 1 is the factor of 21,
96 ÷ 1 = 96, So, 1 is a factor of 96.
31 x 1 = 31, So, 1 is the factor of 31.
Property (2):
Every number is a factor of zero (0)
As, 7 x 0 = 0,
17 x 0 = 0,
93 x 0 = 0
So, 7, 17, 93, ……, etc., are the factors of 0.
Property (3):
1 is the smallest factor of every number.
1 is the smallest factor of a multiple and the greatest factor of a multiple is the multiple itself.
A number is a factor of itself. SO, a number itself is its own greatest factor. For example 73 ÷ 1 = 73 so, 73 and 1 are the factors. 73 is the greatest factors.
Property (4):
Every number other than 1 has at least two factors, namely the number itself and 1.
We know that 1 and the number itself are always the factors of every number. This means that every number has at least 2 factors.
Therefore, the properties of factors are explained above so, that student can understand each property.
Properties of Factors
Property 1: A number has a finite number of factors.
Property 2: 1 and the number itself are the factors of every number.
Property 3: 1 is the smallest factor of any number.
Property 4: The number itself is the greatest factor of every number.
Property 5: Factors of a number are always smaller or equal to the number.
Property 6: Every factor of a number is the exact divisor of the number.
To find that whether a number is a factor of another number, we divide the bigger number by the smaller number. If the remainder is zero, we say that the divisor is a factor of the dividend.
For example:
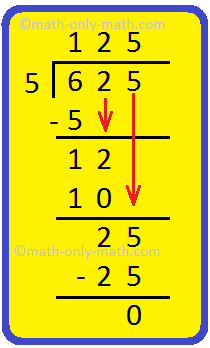
1. Is 5 a factor of 625?
Here, 5 divides 625 exactly. So 5 is a factor of 625.
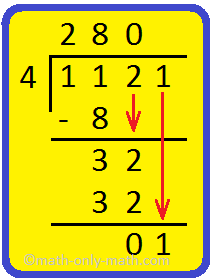
2. Is 4 a factor of 1121?
Here, 4 does not divide 1121 exactly. So 4 is not a factor of 1121.
You might like these
Magic Square | Add upto 15 | Add upto 27 | Fibonacci Sequence | Videos
In a magic square, every row, column and each of the diagonals add up to the same total. Here is a magic square. The numbers 1 to 9 are placed in the small squares in such a way that no number is repe
Division by 10 and 100 and 1000 |Division Process|Facts about Division
Division by 10 and 100 and 1000 are explained here step by step. when we divide a number by 10, the digit at ones place of the given number becomes the remainder and the digits at the remaining places of the number given the quotient.
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Division by Two-Digit Numbers | Knowledge of Estimation | Division
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowledge of estimation to find the actual quotient. 1. Divide 94 by 12
Subtraction | How to Subtract 2-digit, 3-digit, 4-digit Numbers?|Steps
The answer of a subtraction sum is called DIFFERENCE. How to subtract 2-digit numbers? Steps are shown to subtract 2-digit numbers.
Subtraction with Regrouping | 4-Digit, 5-Digit and 6-Digit Subtraction
We will learn subtraction 4-digit, 5-digit and 6-digit numbers with regrouping. Subtraction of 4-digit numbers can be done in the same way as we do subtraction of smaller numbers. We first arrange the numbers one below the other in place value columns and then we start
Division of Four-Digit by a One-Digit Numbers | Worksheet with Answer
In division of four-digit by a one-digit numbers are discussed here step by step. How to divide 4-digit numbers by single-digit numbers?
Word Problems on Division | Examples on Word Problems on Division
Word problems on division for fourth grade students are solved here step by step. Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. How much money will each person get?
Subtraction without Regrouping |4-Digit, 5-Digit & 6-Digit Subtraction
We will learn subtracting 4-digit, 5-digit and 6-digit numbers without regrouping. We first arrange the numbers one below the other in place value columns and then subtract the digits under each column as shown in the following examples. 1. Subtract 3248 from 6589.
Multiply a Number by a 2-Digit Number | Multiplying 2-Digit by 2-Digit
How to multiply a number by a 2-digit number? We shall revise here to multiply 2-digit and 3-digit numbers by a 2-digit number (multiplier) as well as learn another procedure for the multiplication of 3-digit, 4-digit, etc., numbers by a 2-digit multiplier.
Place Value and Face Value | Place and Face Value of Larger Number
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expressing Place Value and Face Value | International & Indian System
We will learn expressing place value and face value of a digit in any number in International and Indian system. Place value: We know how to find out the place value of a digit in any number.
Multiplication | How to Multiply a One, Two or Three-digit Number?
In multiplication we know how to multiply a one, two or three-digit number by another 1 or 2-digit number. We also know how to multiply a four-digit number by a 2-digit number. We also know the different methods of multiplication. Here, we shall make use of the methods and
Indian Numbering System | Ones Period | Thousands Period |Lakhs Period
In the Indian numbering system, we use different periods like ones, thousands, lakhs, crores, etc. Suppose, let us understand the Indian system by using number 1: ones (1), tens (10), hundreds (100)
Dividing 3-Digit by 1-Digit Number Video | Long Division | Worksheet
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit number. I: Dividing 3-digit Number by 1-Digit Number without Remainder:
Related Concept
● Factors and Multiples by using Multiplication Facts
● Factors and Multiples by using Division Facts
● Factors
● Even and Odd Numbers Between 1 and 100
● Examples on Even and Odd Numbers
4th Grade Math Activities
From Properties of Factors to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
May 07, 25 01:48 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
May 07, 25 01:33 AM
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima… -
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
May 06, 25 01:23 AM
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by… -
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
May 06, 25 12:01 AM
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps -
Word Problems on Decimals | Decimal Word Problems | Decimal Home Work
May 05, 25 01:27 AM
Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.