Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Multiples
Multiples of a number is discussed here.
Let us recall
The numbers 1, 2, 3, 4, ........... are called Natural Numbers (N).
The numbers 0, 1, 2, 3, 4, ............. are called Whole Numbers (W)
That is [N + zero = W]
The numbers like 2, 4, 6, 8, .............. that are exactly divisible by two are called Even Numbers.
The numbers like 1, 3, 5, 7, .............. that are not divisible by two are called Odd Numbers.
We know about the whole numbers: ‘the numbers starting from 0 and having the pattern 0, 1, 2, 3, 4, 5, up to infinity, are called whole numbers.
The whole numbers minus 0 are the natural numbers.
All the natural numbers are multiples of 1.
Multiples:
What are multiples?
‘The product obtained on multiplying two or more whole numbers is called a multiple of that number or the numbers being multiplied.’
Any number can be represented as a multiple of each factor.
Thus, 18 is the multiple of 1, 2, 3, 6, 9 and 18.
REMEMBER
The meaning of least common multiple:
Least - Lowest
Common - Something which is shared or in common
Multiple - What you get when you multiply
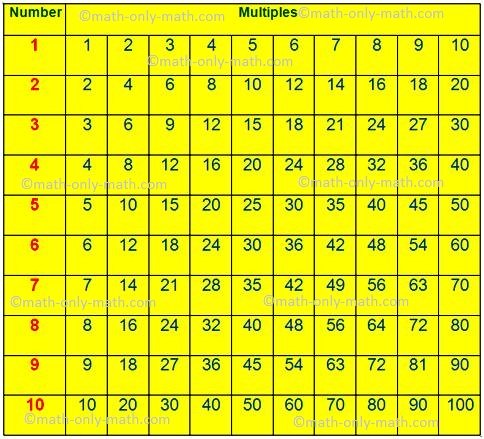
There is no end to multiples of any number. The first ten multiples of the numbers starting from 1 to 10 are given here.
First Ten Multiples of the Numbers
In the above table we can observe the first ten multiples of the numbers starting from 1 to 10.
A multiple is the product of a number and any other number.
Understanding Multiples
1. The first multiple of a number is the number itself.
2. Every number is a multiple of 1.
3. 0 is a multiple of every number.
4. Multiples of a number are infinite (you can carry on writing them).
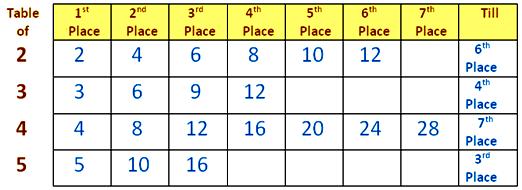
Multiples are really the products of the tables that you learn.
Sometimes, you learn the multiples till the 10th place or the 12th place of every number table but multiples are really infinite.
Take a look at the multiples of different numbers:
We know that when two numbers are multiplied the result is called the product or the multiple of given numbers. For example, if we multiply 4 and 5 the result 20 is a multiple of 4 ad 5.
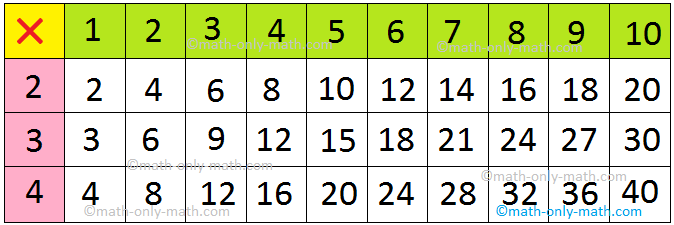
Le us find the first 10 multiples of 2, 3 and 4. We multiply the numbers by the counting numbers 1, 2, 3, 4, …. to get the multiples.
The first 10 multiples of 2 are: 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20
The first 10 multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27 and 30
The first 10 multiples of 2 are: 4, 8, 12, 16, 20, 24, 28, 32, 36 and 40
We can find as many multiples of a number as we like.
More explanation of multiples with examples:
Eight multiplied by one 8 × 1 = 8
Eight multiplied by two 8 × 2 = 16
Eight multiplied by three 8 × 3 = 24
Here the numbers 8, 16, 24, .......... are obtained on multiplying 8 by 1, 2, 3, ......
Hence 8, 16, 24, ........ are called multiples of 8.
Look at the multiplication fact 8 × 3 = 24
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, .........
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ..........
Here, 24 is a multiple of 8 as well as 3.
Hence 24 is also called the product of 8 and 3.
The products obtained by multiplying a number by 1, 2, 3, ........... are called the multiples of that number.
Multiples of 2:
2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10 and so on.
2, 4, 6, 8, 10, ........... are the multiples of 2.
Similarly,
Multiples of 3 : 3, 6, 9, 12, 15, ...............
Multiples of 4 : 4, 8, 12, 16, 20, ...............
Multiples of 5 : 5, 10, 15, 20, 25, ...............
For example:
1. Is 15 a multiple of 5?
Yes, since 15 = 3 × 5
2. Is 28 a multiple of 7?
Yes, since 28 = 7 × 4
3. Is 34 a multiple of 8?
No, since 8 × ........ = 34
(We cannot replace the blank by any number.)
Properties of Multiples:
I. Every number is a multiple of itself.
(i) 2 = 2 × 1
(ii) 3 = 3 × 1
(iii) 4 = 4 × 1
(iv) 5 = 5 × 1 and so on.
II. Every number is a multiple of 1.
(i) 8 = 1 × 8
(ii) 9 = 1 × 9
(iii) 10 = 1 × 10
(iv) 11 = 1 × 11 and so on.
III. A multiple of a number either equals or is greater than the number.
Multiple of 6: 6, 12, 18, 24, ...........
Multiple of 7: 7 14, 21, 28, ...........
IV. Every multiple of 2 is an even number.
Multiple of 2, 4, 6, 8, 10, 12, 14, 16, 18, ........ All are even number.
A number which is not a multiple of 2 is an odd number.
For example, 1, 3, 5, 7, ........
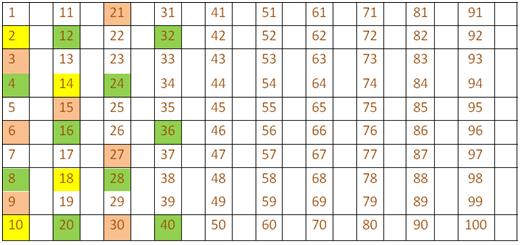
Common Multiple
Take a look at the multiples of 2, 3, 4, till the 10th place.
Multiples of 2 are in yellow; 3 are in orange; 4 are in light green.
When a number is multiple of 2 or more numbers it is called a common multiple.
Common multiples of 2 and 3 are 6, 12, 18 till the 10th place.
Common multiple of 2, 3 and 4 till the 10th place is → 12.
Frequently Asked Questions (FAQs)
1. What Is a Multiple in Math?
Answer:
Multiples are the products you get when a number is multiplied by itself and other numbers as well. Also, multiples are the numbers obtained by skip counting.
Example: Let us recall the multiplication table of 4.
The products 4, 8, 12 and 16 are the multiple of 4.
2. Find the first three multiples of 5.
Answer:
We will multiply 5 by 1, 2 and 3.
5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
So, 5, 10, 15 are the first 3 multiples of 5.
3. Write the first five multiples of 7.
Answer:
To find the first five multiples of 7, we multiply 7 by 1, 2, 3, 4, 5.
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
Therefore, the first five multiples of 7 are 7, 14, 21, 28 and 35.
4. Find the first four multiples of 6.
Answer:
We know, 6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
Hence, the first 4 multiples of 6 are 6, 12, 18 and 24.
5. Write the first 6 multiples of 15.
Answer:
We know, 15 × 1 = 15
15 × 2 = 30
15 × 3 = 45
15 × 4 = 60
15 × 5 = 75
15 × 6 = 90
Hence, the first 6 multiples of 15 are 15, 30, 45, 60, 75 and 90.
7. How do you know that 24 is a multiple of 3 and 8 but not of 7?
Solution:
24 = 3 × 8 + 0; 24 = 8 × 3 + 0; 24 = 7 × 3 + 3
From the above divisions, we can say that 24 is the multiple of 3 and 8, but not of 7.
Note: A multiple is completely divisible by its factor.
Worksheet on Multiples:
I. Fill in the blanks:
(i) 14 is a multiple of 2 and ............
(ii) If 25 × 4 = 100; 100 is a multiple of ............ and ............
(iii) If 9 × 8 = 72; 72 is the ............ of 9 and 8.
(iv) ............ is a multiple of 7 and 3.
(v) If 2 × 5 × 10 = 100; 100 is a multiple of ............, ............ and ............
Answer:
I. (i) 7
(ii) 4 and 25
(iii) multiple
(iv) 21
(v) 2, 5 and 10
II. Is the first number a multiple of the second number in the following pairs of numbers?
(i) (4, 2)
(ii) (18, 5)
(iii) (61, 1)
(iv) (17, 4)
(v) (36, 12)
(vi) (40, 8)
Answer:
II. (i) Yes
(ii) No
(iii) Yes
(iv) No
(v) Yes
(vi) Yes
III. Answer the following questions:
(i) What is the smallest number which, when added to an even number, makes the sum an odd number?
(ii) What is the smallest number which, when subtracted from an even number gives an odd number?
(iii) Circle all the even numbers and cross all the odd numbers.
3, 8, 11, 19, 22, 38, 41, 56, 63, 74, 76, 85, 89, 92, 95, 99
(iv) Find the first four multiples of
(i) 6
(ii) 7
(iii) 9
(iv) 8
(v) 12
Answer:
III. (i) 1
(ii) 1
(iii) Circle all the even numbers and cross all the odd numbers.
Even Numbers: 8, 22, 38, 56, 74, 76, 92
Odd Numbers: 3, 11, 19, 41, 63, 85, 89, 95, 99
(iv) (i) 6, 12, 18, 24
(ii) 7, 14, 21, 28
(iii) 9, 18, 27, 36
(iv) 8, 16, 24, 32
(v) 12, 24, 36, 48
IV. Write the next four multiples:
(i) 12, 24, 36, _____, _____, _____, _____.
(ii) 13, 26, 39, _____, _____, _____, _____.
(iii) 14, 28 ,42, _____, _____, _____, _____.
(iv) 11, 22, 33, _____, _____, _____, _____.
Answer:
IV. (i) 48, 60, 72, 84
(ii) 52, 65, 78, 91
(iii) 56, 70, 84, 98
(iv) 44, 55, 66, 77
V. Answer the following questions:
(i) Is 144 a multiple of 16?
(ii) Is 169 a multiple of 14?
(iii) Is 168 a multiple of 21?
(iv) Is 72 a multiple of 9?
(v) Find the first four multiples of 6.
(vi) Find the first five multiple of 8.
(vii) Find the first three multiples of 14.
(viii) Is 220 a multiple of 25?
Answer:
V. (i) Yes
(ii) No
(iii) Yes
(iv) Yes
(v) 6,12, 18, 24
(vi) 8, 16, 24, 32, 40
(vii) 14, 28, 42
(viii) No
VI. Fill in the blanks:
(i) 13 × 14 = 182 means _____ is a multiple of 13 and 14?
(ii) 15 × 18 = 270 means 270 is a multiple _____ and _____.
(iii) 12 × 13 = 156 means 156 is a multiple of _____ and _____.
(iv) 12 × 8 = 96 means 96 is a multiple of _____ and _____.
Answer:
VI.
1. 182
2. 15 and 18
3. 12 and 13
4. 12 and 8
VII. Write the 8th multiple of each of the following.
(i) 4
(ii) 5
(iii) 11
(iv) 7
(v) 13
Answer:
VII. (i) 32
(ii) 40
(iii) 88
(iv) 56
(v) 104
Related Concept
● Factors and Multiples by using Multiplication Facts
● Factors and Multiples by using Division Facts
● Factors
● Even and Odd Numbers Between 1 and 100
● Examples on Even and Odd Numbers
4th Grade Math Activities
From Multiples to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

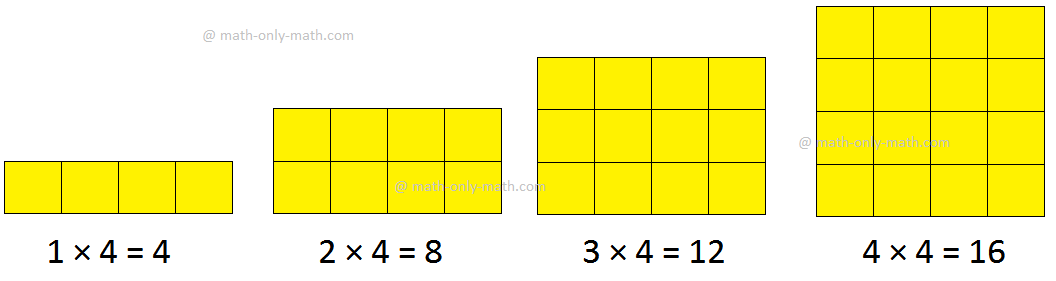



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.