Factors and Multiples by using Division Facts
Factors and multiples by using division facts are explained here. With
the help of this operation we shall learn some other terms.
Consider the following factors and multiples by using division facts:
(i)
15 is not completely divisible by 2
i.e., 14 ÷ 2 = 7 or dividend ÷ divisor = quotient
When
a number (dividend) is completely divided by another number (divisor),
then this divisor is called a factor and the dividend is called a
multiple of the divisor.
Here 2 is the factor of the multiple 14.
14 ÷ 1 = 14, 14 ÷ 14 = 1, 14÷ 7 = 2
So the divisors 1, 14 and 7 are also the complete divisors or factors of the dividend (multiple) 14.
Thus, the factor must be a complete divisor of the multiple (dividend).
(ii) 18 ÷ 2 = 9,
18 ÷ 3 = 6,
18 ÷ 9 = 2,
18÷ 6 = 3,
18 ÷ 1 = 18,
18 ÷ 18 = 1
If 18 are divided by 2, 3, 9, 6, 1 and 18, it is completely divided.
Thus, 2, 3, 9, 6, 1, 18 or 1, 2, 3, 6, 9 and 18 are the complete divisors or the factors of the multiple 18.
We may define a factor as the multiplier or complete divisor of its multiple.
A multiple has many but limited numbers of factors.
35 have 4 factors, i.e., 1, 5, 7 and 35.
42 have 8 factors, i.e., 1, 2, 3, 6, 7, 14, 21 and 42.
(iii) Let us find the factors of 24.
By division method
24 ÷ 1 = 24
24 ÷ 2 = 12
24 ÷ 3 = 8
24 ÷ 4 = 6
1, 2, 3, 4, 6, 8, 12 and 24 are the factors of 24
Taking help of division to check multiples
(i) Is 24 a multiple of 8? Use division.
24 ÷ 8 = 3 (No remainder)
Yes, 24 is a multiple of 8.
(ii) Is 56 a multiple of 5? Use division.
56 ÷ 5
Here remainder is 1
56 is not a multiple of 5 because there is a remainder.
(iii) Is 456 a multiple of 9? Use division.
456 ÷ 9
Here remainder is 6
456 is not a multiple of 9 because there is a remainder.
Note:
In division if there is no remainder, the dividend is the multiple of the divisor.
Finding the factors of a number through division
(i) Take a look. Is 5 a factor of 15?
15 ÷ 5 = 3 15 ÷ 3 = 5
No remainder No remainder
5 is factor of 15. 3 is a factor of 15.
Both 3 and 5 are factor of 15.
(ii) Find the factors of 36:
1 × 36 = 36 2 × 18 = 36 3 × 12 = 36
4 × 9 = 36 5 is not a factor of 36 6 × 6 = 36
Note:
No need to do any more division because the factors are getting repeated.
Now we can write the factors like this:
The factors of 36 are:
1 × 36 = 36
2 × 18 = 36
3 × 12 = 36
4 × 9 = 36
6 × 6 = 36
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
Note:
It is very important to work systematically in math.
(iii) Is 7 a factor of 24?
24 ÷ 7 = 3 remainder 3
Here, remainder = 3
7 is not a factor of 24.
Taking help of division to check multiples
(i) Is 24 a multiple of 8? Use division.
24 ÷ 8 = 3 (No remainder)
Yes, 24 is a multiple of 8.
(ii) Is 56 a multiple of 5? Use division.
56 ÷ 5
Here remainder is 1
56 is not a multiple of 5 because there is a remainder.
(iii) Is 456 a multiple of 9? Use division.
456 ÷ 9
Here remainder is 6
456 is not a multiple of 9 because there is a remainder.
You might like these
-
In 4th grade factors and multiples worksheet we will find the factors of a number by using multiplication method, find the even and odd numbers, find the prime numbers and composite numbers, find the prime factors, find the common factors, find the HCF(highest common factors
-
Examples on multiples on different types of questions on multiples are discussed here step-by-step. Every number is a multiple of itself. Every number is a multiple of 1. Every multiple of a number is either greater than or equal to the number. Product of two or more numbers
-
In worksheet on word problems on H.C.F. and L.C.M. we will find the greatest common factor of two or more numbers and the least common multiple of two or more numbers and their word problems. I. Find the highest common factor and least common multiple of the following pairs
-
Let us consider some of the word problems on l.c.m. (least common multiple). 1. Find the lowest number which is exactly divisible by 18 and 24. We find the L.C.M. of 18 and 24 to get the required number.
-
Let us consider some of the word problems on H.C.F. (highest common factor). 1. Two wires are 12 m and 16 m long. The wires are to be cut into pieces of equal length. Find the maximum length of each piece. 2.Find the greatest number which is less by 2 to divide 24, 28 and 64
-
The least common multiple (L.C.M.) of two or more numbers is the smallest number which can be exactly divided by each of the given number. The lowest common multiple or LCM of two or more numbers is the smallest of all common multiples.
-
Common multiples of two or more given numbers are the numbers which can exactly be divided by each of the given numbers. Consider the following. (i) Multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, …………etc. Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, …………… etc.
-
In worksheet on multiples of that numbers, all grade students can practice the questions on multiples. This exercise sheet on multiples can be practiced by the students to get more ideas on the numbers that are being multiplied. 1. Write any four multiples of: 7
-
Prime factorisation or complete factorisation of the given number is to express a given number as a product of prime factor. When a number is expressed as the product of its prime factors, it is called prime factorization. For example, 6 = 2 × 3. So 2 and 3 are prime factors
-
Prime factor is the factor of the given number which is a prime number also. How to find the prime factors of a number? Let us take an example to find prime factors of 210. We need to divide 210 by the first prime number 2 we get 105. Now we need to divide 105 by the prime
-
The properties of multiples are discussed step by step according to its property. Every number is a multiple of 1. Every number is the multiple of itself. Zero (0) is a multiple of every number. Every multiple except zero is either equal to or greater than any of its factors
-
What are multiples? ‘The product obtained on multiplying two or more whole numbers is called a multiple of that number or the numbers being multiplied.’ We know that when two numbers are multiplied the result is called the product or the multiple of given numbers.
-
Practice the questions given in the worksheet on hcf (highest common factor) by factorization method, prime factorization method and division method. Find the common factors of the following numbers. (i) 6 and 8 (ii) 9 and 15 (iii) 16 and 18 (iv) 16 and 28
-
In this method we first divide the greater number by the smaller number. The remainder becomes the new divisor and the previous divisor as the new dividend. We continue the process until we get 0 remainder. Finding highest common factor (H.C.F) by prime factorization for
-
We will discuss here about the method of h.c.f. (highest common factor). The highest common factor or HCF of two or more numbers is the greatest number which divides exactly the given numbers. Let us consider two numbers 16 and 24.
Related Concept
● Factors
and Multiples by using Multiplication Facts
● Factors
and Multiples by using Division Facts
● Multiples
● Properties of
Multiples
● Examples on
Multiples
● Factors
● Factor Tree Method
● Properties of
Factors
● Examples on
Factors
● Even and Odd
Numbers
● Even
and Odd Numbers Between 1 and 100
● Examples
on Even and Odd Numbers
4th Grade Math Activities
From Factors and Multiples by using Division Facts to HOME PAGE
Didn't find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
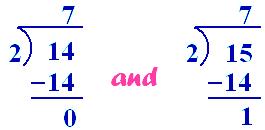
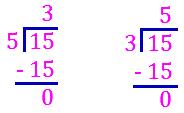
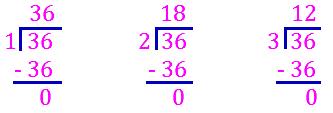
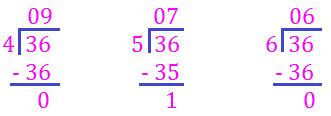
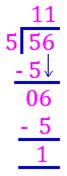
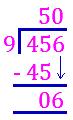
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.