Even and Odd Numbers
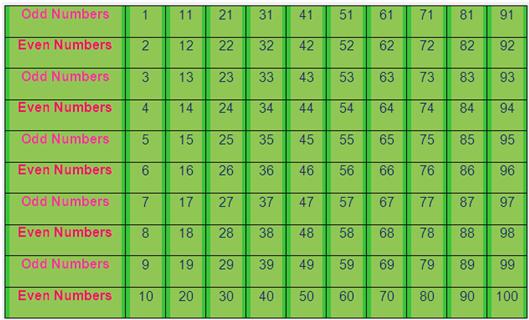
Between 1 and 100

All the even and odd numbers between 1 and 100 are discussed here.

Even and Odd Numbers:

Two objects which share some kind of relationship, are said to be pairs.

Some objects can be put into pairs.

10 marbles can be put into 5 pairs.

Some objects cannot be put into pairs.

7 marbles can not be put into pairs.

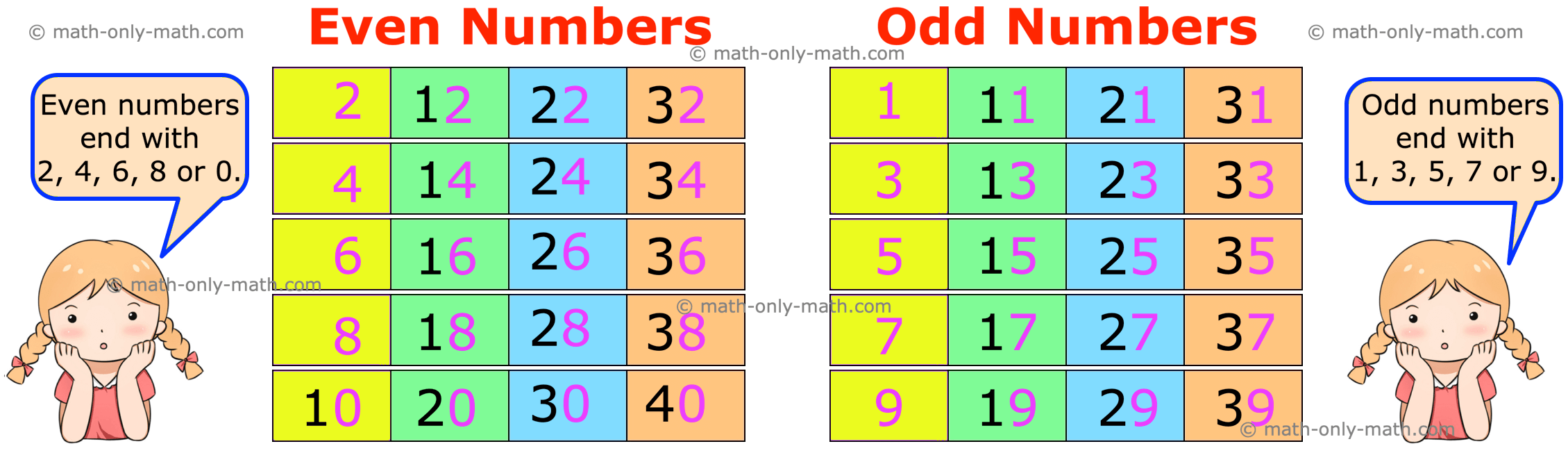
Numbers that can put into pairs are called even numbers.

Numbers like 2, 4, 6, 8, 10, 12, ..... are even numbers.

Even numbers have the digits 0, 2, 4, 6 or 8 at the ones place.

Numbers that cannot be put into pairs are called odd numbers.

Numbers like 1, 3, 5, 7, 9, 11, .... are odd numbers.

Odd numbers have the digits 1, 3, 5, 7, 9 at the ones place.

Remember:

• All numbers can be grouped either in odd or in even numbers.

• We can get an odd number by adding 1 to an even number and vice-versa.

Even Numbers:

A number which is a multiple of 2 is called an even number.

or

A number is even, if it is divisible by 2 or 2 is a factor of it.

Thus 2, 4, 6, 8, 10, 12, are even numbers.

REMEMBER

● Even numbers always end in 0, 2, 4, 6, 8.

● 2 is the smallest prime number and also the only even prime number. All other even numbers are composite

Let us see the following example of even numbers:

14 grains of wheat are shown below. Let us make their pairs.

All the 14 grains can be paired. Numbers that can be paired are called even numbers. Hence, 14 is an even number.

Some more examples of even numbers are 12, 24, 46, 68 and 80.

Solved Examples on Even Numbers:

1. Write all the even numbers from 2 to 20.

Solution:

All the even numbers from 2 to 20 are 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20.

Odd Numbers:

A number which is not a multiple of 2 is called an odd number.

or

A number is odd, if it is not divisible by 2.

Thus 1, 3, 5, 7, 9, 11, .... are odd numbers.

Any even number + 1 odd number i.e., if we divide any odd number by 2, we get 1 as remainder.

REMEMBER

● Odd numbers always end in 1, 3, 5, 7, 9.

Let us see the following example of odd numbers:

Now, look at the 13 grains of maize shown below. Let us try to make their pairs also.

All the 13 grains can not be paired. Numbers that cannot be paired are called odd numbers. Hence, 13 is an odd number.

Some more examples of odd numbers are 11, 23, 55, 87 and 99.

Solved Examples on Odd Numbers:

1. Find all the odd numbers from 1 to 17.

Solution:

All the odd numbers from 1 to 17 are 1, 3, 5, 7, 9, 11, 13, 15 and 17.

What are the even numbers from 1 to 100?

The even numbers from 1 to 100 are:

 2             4             6             8           10

12           14           16           18           20

22           24           26           28           30

32           34           36           38           40

42           44           46           48           50

52           54           56           58           60

62           64           66           68           70

72           74           76           78           80

82           84           86           88           90

92           94           96           98           100

What are the odd numbers from 1 to 100?

The odd numbers from 1 to 100 are:

 1             3             5             7             9

11           13           15           17           19

21           23           25           27           29

31           33           35           37           39

41           43           45           47           49

51           53           55           57           59

61           63           65           67           69

71           73           75           77           79

81           83           85           87           89

91           93           95           97           99

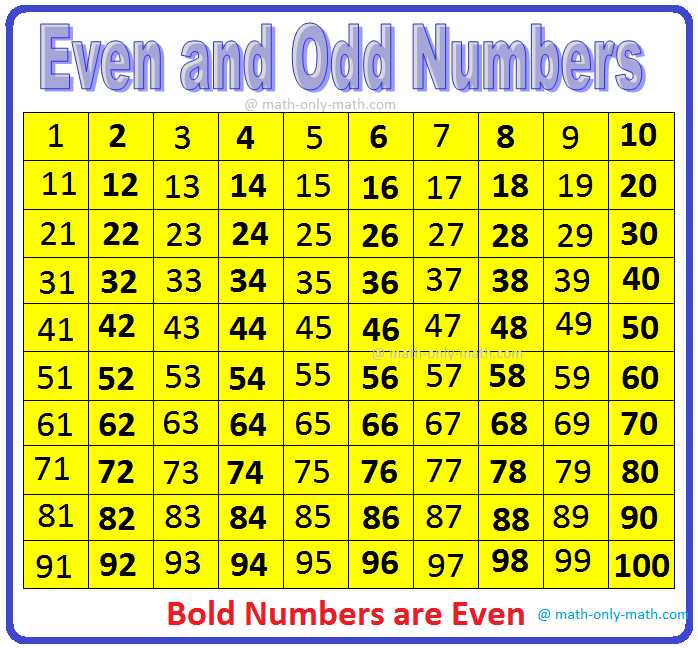
Even and Odd  Numbers

In the following table, bold numbers are even numbers and the remaining numbers are add numbers.

Properties of Even and Odd Numbers:

1. (i) Every number coming after an even number is an odd number

12 + 1 = 13

16 +1 = 17

176 + 1 = 177

216 + 1 = 217

(ii) Every number coming after an odd number is an even number

15 + 1 = 16

19 + 1 = 20

205 + 1 = 206

419 + 1 = 420

2. Every number having 2, 4, 6, 8 and 0 at its one’s place is divisible by 2 and hence, an even number.

3. No number having 3, 5, 7 and 9 at its one's place is divisible by 2 and hence, an odd number.

4. All the even and odd numbers are whole numbers.

Even numbers can be put in pairs (groups of 2).

6 is even.

Odd numbers have one left over when you put them in pairs.

7 is odd.

Worksheet on Even and Odd Numbers:

1. Write all the even numbers between 35 and 55.

Answer:

36, 38, 40, 42, 44, 46, 48, 50, 52, 54.

2. write all the odd numbers  between 40 and 70.

Answer: 

41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69.

3. Write E for even and O for odd number in the box.

(i) 3     ▢

(ii) 20     ▢

(iii) 38     ▢

(iv) 69      ▢

(v) 8     ▢

(vi) 27     ▢

(vii) 42     ▢

(viii) 73     ▢

(ix) 9     ▢

(x) 30     ▢

(xi) 49     ▢

(xii) 87     ▢

(xiii) 11     ▢

(xiv) 31     ▢

(xv) 50     ▢

(xvi) 90     ▢

(xvii) 15     ▢

(xviii) 36     ▢

(xix) 62      ▢

(xx) 99     ▢

Answer:

3. (i) O

(ii) E

(iii) E

(iv) O

(v) E

(vi) O

(vii) E

(viii) O

(ix) O

(x) E

(xi) O

(xii) O

(xiii) O

(xiv) O

(xv) E

(xvi) E

(xvii) O

(xviii) E

(xix) E

(xx) O

4. Write the next even number. One has been done for you:

(i) 74        76 

(ii) 56     _____

(iii) 86     _____

(iv) 98     _____

(v) 42     _____

(vi) 60     _____

Answer:

4. (ii) 58

(iii) 88

(iv) 100

(v) 44

(vi) 62

5. Solve the sums. If the answer is even, colour the shape red. If the answer is odd, colour the shape green:

Answer:

5. 

6. Write the next odd number. One has been done for you:

(i) 51        53 

(ii) 65     _____

(iii) 77     _____

(iv) 83     _____

(v) 95     _____

(vi) 55     _____

Answer:

6. (ii) 67

(iii) 79

(iv) 85

(v) 97

(vi) 57

7. Which letters are present in even numbers in these words?

Answer:

7. (i) AHMTC

(ii) RMA

(iii) COMDTO

8. Tick (✔) the odd numbers and cross (x) out the even numbers.

11     14     22     31     39     40

46     52     59     67     68     73

77     85     87     91     93     99

Answer:

8. Even number: 14, 22, 40, 46, 52, 68

Odd Numbers: 11, 31, 39, 59, 67, 73, 77, 85, 87, 91, 93, 99

Related Concept

● Factors and Multiples by using Multiplication Facts

● Factors and Multiples by using Division Facts

● Multiples

● Properties of Multiples

● Examples on Multiples

● Factors

● Factor Tree Method

● Properties of Factors

● Examples on Factors

● Even and Odd Numbers

● Even and Odd Numbers Between 1 and 100

● Examples on Even and Odd Numbers

4th Grade Math Activities

From Even and Odd Numbers Between 1 and 100 to HOME PAGE