Even and Odd Numbers

We will discuss here about the even and odd numbers.

Even Numbers:

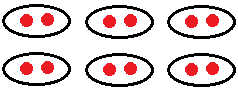
In this picture, there are 12 dots. Let us make pairs we observe that all the dots are paired and no dot is left, so we say 12 is an even number.

In this picture, there are 8 dots and all are paired so 8 is an even number.

In general we can say that all those numbers that can be put into pairs are called even numbers, that is, all those numbers which come in the table of two are even numbers.

Or, we can say those numbers which are exactly divisible by 2 are called even numbers. We can obtain even numbers by multiplying 2 with whole numbers.

As we know that exactly divisible means no remainder is left when we divide a number by another number. If we divide 12 by 2 we get 6 as quotient and no remainder is left. So, 12 is an even number.

There are so many numbers which are divisible by 2. The numbers which are divisible by 2 are the multiples of 2. When we multiply 2 by another number, the product is called a multiple of 2.

For example, 2 × 0 = 0, 2 × 1 = 2, 2 × 2 = 4, 2 × 3 = 6, 2 × 4 = 8, etc.

Hence, even numbers end in 0, 2, 4, 6, 8.

Thus, every multiple of 2 is called an even number or the number which has 2 as one of its factors is known as an even number.

For example, 2, 4, 6, 8, 10……36, 38, 40……etc. are the multiples of 2 or 2 is one of the factors of these numbers.

So, all these numbers are called even numbers.

Thus, any number divisible by 2 is an even number.

Example on Even Numbers:

Find the even numbers between 5 and 15. The numbers between 5 and 158 are: 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

We observe that 6, 8, 10, 12 and 14 are exactly divisible by 2.

So, they are even numbers.

Odd Numbers:

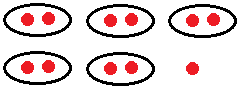
In this picture, there are 11 dots. We observe that all the dots are not paired up. One dot is left unpaired. Such numbers that cannot be put into pairs are called odd numbers.

Or, we can say those numbers which are not exactly divisible by 2 are called odd numbers. Or, we can say that, the number which is not even or not divisible by 2 is called an odd number.

For example, 13 is not exactly divisible by 2 because it leaves 1 as remainder when we divide it by 2. So, 13 is an odd number.

Odd numbers are not the multiples of 2. 

For example, 1, 3, 5, 7, 9, 11, 13, 15, ……., 51, 53, ……., etc., cannot be obtained by multiplying 2 by any other number. They are odd numbers. Hence, odd numbers end in 1, 3, 5, 7, and 9.

Example on Odd Numbers:

Find the odd numbers between 13 and 20. The numbers between 13 and 20 are: 13, 14, 15, 16, 17, 18, 19, 20.

We observe that 13, 15, 17 and 19 are not exactly divisible by 2.

So, they are odd numbers..

A number which is a multiple of 2 is an even number and that which is not multiple of 2 is an odd number.

Two objects form a pair. Thus, one object does not form any pair. If there are three objects, there is one pair and one object is left. If there are four objects, these form two pairs. If there are five objects, these form two pairs and one object is left.

The numbers that make perfect pairs are called even numbers.

For example: 34, 56, 780, 1212, 490

The numbers do not make perfect pairs are called odd numbers.

For example: 79, 851, 233, 2777, 609

Properties of Even and Odd numbers:

1. The sum of two even numbers is always an even number.

For example: 14 + 258 = 272.

2. The sum of two odd numbers is always an even number.

For example: 769 + 147 = 916

3. The sum of one odd and one even numbers is always an odd number.

For example: 67 + 232 = 299

4. Even Numbers ends in 0, 2, 4, 6, 8.

For example: 24 is an even number since 24 ends in 4.

                    120 is an even number since 120 ends in 0.

5. Odd Numbers ends in 1, 3, 5, 7, 9.

For example: 73 is an odd number since 73 ends in 3.

                    129 is an odd number since 129 ends in 9.

Question and Answer on Even and Odd Numbers:

I. Tick (P) the even numbers and cross (û) the odd numbers:

(i) 250

(ii) 123

(iii) 358

(iv) 247

(v) 888

(vi) 129

(vii) 879

(viii) 2577

(ix) 2468

(x) 9003

(xi) 2758

(xii) 6881

(xiii) 1554

(xiv) 5565

(xv) 1747

(xvi) 5568

(xvii) 8785

(xviii) 252

(xix) 2475

(xx) 1454

(xxi) 1297

(xxii) 666

(xxiii) 2199

(xxiv) 2211

Answer:

I. (i) Even Number P

(ii) Odd Number û

(iii) Even Number P

(iv) Odd Number û

(v) Even Number P

(vi) Odd Number û

(vii) Odd Number û

(viii) Odd Number û

(ix) Even Number P

(x) Odd Number û

(xi) Even Number P

(xii) Odd Number û

(xiii) Even Number P

(xiv) Odd Number û

(xv) Odd Number û

(xvi) Even Number P

(xvii) Odd Number û

(xviii) Even Number P

(xix) Odd Number û

(xx) Even Number P

(xxi) Odd Number û

(xxii) Even Number P

(xxiii) Odd Number û

(xxiv) Odd Number û

II. Are the following numbers odd or even?

(i) 2782

(ii) 809

(iii) 2133

(iv) 7605

(v) 170

(vi) 5698

(vii) 6544

(viii) 3999

(ix) 4004

(x) 5000

(xi) 1093

(xii) 22

(xiii) 825

(xiv) 9329

(xv) 6003

(xvi) 1934

(xvii) 1918

(xviii) 431

(xix) 123

(xx) 89

Answer:

II. (i) Even Number

(ii) Odd Number

(iii) Odd Number

(iv) Odd Number

(v) Even Number

(vi) Even Number

(vii) Even Number

(viii) Odd Number

(ix) Even Number

(x) Even Number

(xi) Odd Number

(xii) Even Number

(xiii) Odd Number

(xiv) Odd Number

(xv) Odd Number

(xvi) Even Number

(xvii) Even Number

(xviii) Odd Number

(xix) Odd Number

(xx) Odd Number

Related Concept

● Factors and Multiples by using Multiplication Facts

● Factors and Multiples by using Division Facts

● Multiples

● Properties of Multiples

● Examples on Multiples

● Factors

● Factor Tree Method

● Properties of Factors

● Examples on Factors

● Even and Odd Numbers

● Even and Odd Numbers Between 1 and 100

● Examples on Even and Odd Numbers

4th Grade Math Activities

From Even and Odd Numbers to HOME PAGE