Factors

Factors of a number are discussed here so that students can understand the factors of the product.

What are factors?

We know that the product of 3 and 5 is 15.

3 × 5 = 15. Here, 3 and 5 which exactly divide the number 15.

15 ÷ 3 = 5, 15 ÷ 5 = 3. So, 3 and 5 are called the factors of 15.

Consider another example.

1 × 15 = 15.

1 and 15 also divide 15 exactly. (15 ÷ 1 = 15, 15 ÷ 15 = 1)

So, 1 and 15 are also the factors of 15.

Similarly, 7 × 5 = 35 here, 7 and 5 are the factors of 35.

4 × 8 = 32 here, 4 and 8 are the factors of 32.

We can find several other factors of 32 like, 2 × 16 = 32, 1 × 32 = 32

So, 1, 2, 4, 8, 16 and 32 are the factors of 32. Since they all divide 32 exactly.

When a number divides the other number exactly, the former is called the factor of the later.

We can define factor in the following way also.

When a divisor divides the dividend exactly, the divisor is called a factor of the dividend.

Consider the multiplication fact 6 × 4 = 24

(i) 24 ÷ 4 = 6

(ii) 24 ÷ 6 = 4

Here 6 divides 24 exactly without any remainder.

Also 4 divides 24 exactly without any remainder.

Hence 4 and 6 are called factors of 24.

What are the other factors of 24?

1 × 24 = 24                          

2 × 12 = 24                          

3 × 8 = 24

4 × 6 = 24                            

6 × 4 = 24                            

8 × 3 = 24

12 × 2 = 24                          

24 × 1 = 24

Therefore, 1, 2, 3, 4, 6, 8, 12 and 24 are the factors of 24.

Numbers which divide a given number without any remainder are called factors of that number.

Can you guess, why 5 is not a factor of 24? Here 24 is not exactly divisible by 5.

We can find the factors of a number as follows.

Find the factors of 24.

24 = 1 × 24

24 = 1 × 24

24 = 1 × 24

24 = 1 × 24

Thus, the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.

Remember,

(i) If a dividend, when divided by a divisor, is divided completely then we name the divisor as the factor of the dividend or multiple.

(ii) If two or more numbers are multiplied to get the product, then each of the numbers is known as a factor of the product.

(iii) A number can be formed by multiplying two or more numbers together. The numbers that are multiplied together are called the factors of the number.

(iv) In all the numbers we have a common factor that is 1 since, 1 multiplied by any number the result is always that number. If any number is divided by that same number then we get the result as 1.

Properties of Factors:

I. 1 is a factor of every natural number.

1 × 2 = 2,

1 × 3 = 3,

1 × 4 = 4,

1 × 18 = 18 and so on.

II. Every number is a factor to itself.

Factors of 2 → 1, 2

Factors of 3 → 1, 3 

Factors of 4 → 1, 2, 4

A factor of a number is either less than or equal to that number.

Factors of 5 → 1, 5

Factors of 6 → 1, 2, 3, 6

Note: The least factor of a number is 1 and the greatest is the number itself.

Common Factors:

A number that is a factor of two or more numbers is called a common factor of those numbers.

Example:

1. Write all the common factors of 24 and 18.

Solution:

Factor of 24: 1, 2, 3, 4, 6, 8, 12 and 24

Factors of 18: 1, 2, 3, 6, 9 and 18

Common factors of 24 and 18-1,2,3 and 6

To find the common factors of two or more numbers we will first make a list of the factors of each number.

2. How to find the common factors of 12 and 18?

Common factors of 12 and 18 are 1, 2, 3 and 6.

3. How to find the common factors of 6, 8, 10?

Common factors of 6, 8 and 10 are 1 and 2.


Note for understanding the concept of factors;

(i) The numbers that divide a certain number exactly are the factors of that number.

For example, 9 ÷ 1 = 9, 9 ÷ 3 = 3, 9 ÷ 9 = 1 because 9 is exactly divisible by 1, 3 and 9. So, they are the factors of 9.

(ii) 1 is the only number with one factor.

For example, 1 × 1 = 1

(iii) 1 is a factor of every whole number.

For example, 1 × 5 = 5, 1 × 7 = 7 here, 1 is the factor of 5 and 7.

(iv) The smallest factor of a number is 1.

For example, 1 × 5 = 5 here, 1 is the smallest factor of 5

(v) The greatest factor of a number is the number itself.

For example, 1 × 3 = 3 here, 4 is a factor of 4.

(vi) All number (except 1) have two or more than two factors.

For example, 1 × 2 = 2 here, 1 and 2 are the factors of 2

1 × 4 = 4 and 2 × 2 = 4 here, 1, 2 and 4 are the factors of 4.

Observe the following:

1. 6 × 8 = 48 implies 48 is a multiple of 6 and 8.

We also call 6 and 8 as factors of 48.

2. 8 × 9 = 72 implies 72 is a multiple of 8 and 9.

We also call 8 and 9 as factors of 72

3. 14 × 6 = 84 implies 84 is a multiple of 14 and 6.

We also call 14 and 6 as factors of 84

                                   6 × 8 = 48

6 and 8 are factors of 48;            48 is a multiple of 6 and 8

Again,

                                     12 × 9 = 108

12 and 9 are factors of 108                108 is a multiple of 12 and 9

Thus, we can say that when two or more numbers are multiplied, then each number a factor of the product and the product is a multiple of each one of the numbers.

Observe the following:

8 × 6 = 48 implies 8 and 6 are factors of 48.

Also corresponding to the multiplication fact 8 × 6 = 48, we have two division facts 48 ÷ 8 = 6 and 48 ÷ 6 = 8

Here, 8 divides 48 exactly and 6 divides 48 exactly.

Hence, a number is a factor of the other if the first divides the second number exactly Or a number is a factor of the other if the second number is divisible by the first.

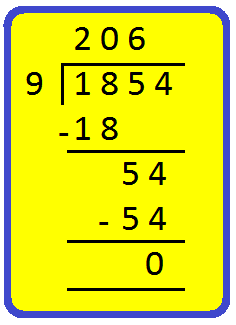
1. Is 9 a factor of 1854?

Solution:

Here 9 divides 1,854 exactly. So 9 is a factor of 1,854.

2. Find all the factors of 18

Solution:

18 = 1 × 18

18 = 2 × 9

18 = 3 × 6

Hence, all the factors of 18 are 1, 2, 3, 6, 9 and 18.

3. Find all the factors of 45.

Solution:

45 = 1 × 45

45 = 3 × 15

45 = 5 × 9

Hence, all the factors of 45 are 1, 3, 5, 9, 15 and 45.

Worksheet on Factors:

I. Fill in the blanks:

(i) 3 and 6 are the .............. of 18.

(ii) .............. is a factor of every number.

(iii) Every number is a factor of ..............

(iv) If 10 × 6 = 60, then ............ and ............ are factors of ............

(v) The greatest factor of 463 is ..............

Answer:

I. (i) factors

(ii) 1

(iii) itself

(iv) 6, 10, 60

(v) 463 itself

II. Write whether the following statements are true or false.

(i) The factor of a number divides the number exactly.

(ii) The factor of a number is always greater than the number.

(iii) If 3 is factor of 6 and 6 is a factor of 12, then 3 is a factor of 12.

(iv) Each number has a finite number of factors.

(v) Every number is a factor of itself.

Answer:

II. (i) True

(ii) False

(iii) True

(iv) False

(v) True

III. Write all the factors of the given numbers.

(i) 36

(ii) 18

(iii) 24

(iv) 15

(v) 60

Answer:

III. (i) All the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

(ii) All the factors of 18 are 1, 2, 3, 6, 9 and 18.

(iii) All the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.

(iv) All the factors of 15 are 1, 3, 5 and 15.

(v) All the factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

IV. Is the first number a factor of the second in the following pairs?

(i) (3, 30)

(ii) (4, 14)

(iii) (6, 24)

(iv) (5, 45)

(v) (8, 70)

(vi) (4, 35)

(vii) (9, 18)

(viii) (7, 91)

Answer:

IV. (i) Yes

(ii) No

(iii) Yes

(iv) Yes

(v) No

(vi) No

(vii) Yes

(viii) Yes

V. Which of the following has 5 as a factor?

(i) 48

(ii) 35

(iii) 25

(iv) 54

(v) 50

Answer:

V. (ii) 35

(iii) 25

(v) 50

Related Concept

● Factors and Multiples by using Multiplication Facts

● Factors and Multiples by using Division Facts

● Multiples

● Properties of Multiples

● Examples on Multiples

● Factors

● Factor Tree Method

● Properties of Factors

● Examples on Factors

● Even and Odd Numbers

● Even and Odd Numbers Between 1 and 100

● Examples on Even and Odd Numbers

4th Grade Math Activities

From Factors to HOME PAGE