Least Common Multiple (L.C.M.)
The least common multiple (L.C.M.) of two or more numbers is the smallest number which can be exactly divided by each of the given number.
Least common multiple (L.C.M.) is also known as lowest common multiple (L.C.M.)
Two or more numbers may have unlimited multiples. The least of them is known as the Least Common Multiple (LCM).
Let us discuss the three methods to find the LCM of two or more numbers.
Method 1: Finding the LCM through Multiples
Working Rules for Finding the LCM through Multiples:
Step I: Find the multiples of the given numbers to such an extent, so as to obtain the smallest common multiple of the given numbers.
Step II: The smallest common multiple found in step 1 is the required LCM of the given numbers.
1. Let us find the L.C.M. of 2, 3 and 4.
Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, ...... etc.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...... etc.
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, ...... etc.
Common multiples of 2, 3 and 4 are 12, 24, 36, ...... etc.
Therefore, the smallest common multiple or least common multiples of 2, 3 and 4 is 12.
We know that the lowest common multiple or LCM of two or more numbers is the smallest of all common multiples.
2. Let us consider the numbers 28 and 12
Multiples of 28 are 28, 56, 84, 112, …….
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, …….
The lowest common multiple (LCM) of 28 and 12 is 84.
3. Find the LCM of 4, 8 and 12.
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ......
Multiples of 8 ate 8, 16, 24, 32, 40, 48, 56, 64, 72, ......
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, ......
Common multiples of 4, 8 and 12 are 24, 48, 72, ......
Lowest common multiple of 4, 8 and 12 = 24.
Therefore, the LCM of 4, 8 and 12 is 24
4. Let us consider the first six multiples of 4 and 6.
The first six multiples of 4 are 4, 8, 12, 16, 20, 24
The first six multiples of 6 are 6, 12, 18, 24, 30, 36
The numbers 12 and 24 are the first two common multiples of 4 and 6. In the above example the least common multiple of 4 and 6 is 12.
Hence, the least common multiple or LCM is the smallest common multiple of the given numbers.
Consider the following.
(i) 12 is the least common multiple (L.C.M) of 3 and 4.
(ii) 6 is the least common multiple (L.C.M) of 2, 3 and 6.
(iii) 10 is the least common multiple (L.C.M) of 2 and 5.
The least or lowest common multiple (in short LCM) of two or more numbers is smallest number which is divisible by each of the given numbers.
4. Find the LC.M. of 12 and 18.
Solution:
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84 ........
Multiples of 18 are 18, 36, 54, 72, 90 .........
Thus, common multiples of 12 and 18 are 36, 72,.....
There, L.C.M. of 12 and 18 is 36.
We can also find the L.C.M. of given numbers by their complete factorization.
Method 1: Finding the LCM by Factorization:
Working Rules for Finding the LCM by Factorization:
Step I: Factorize all the given numbers.
Step II: Find the product of all the factors taking maximum repetition of any factor.
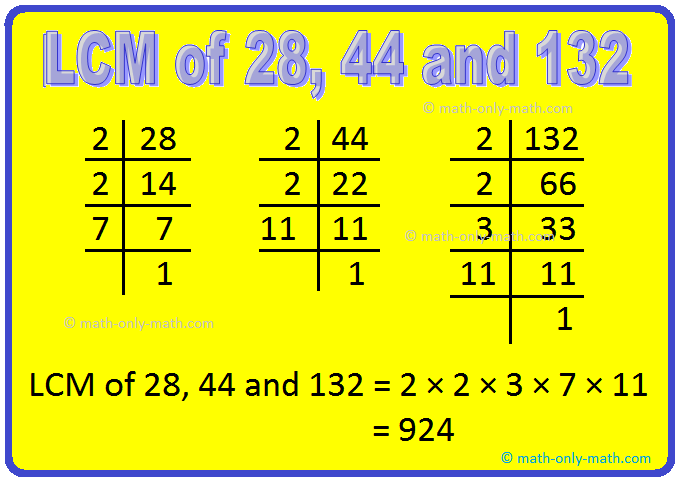
1. Find the LCM of 28, 44 and 132 by prime factorization method.
Solution:
Prime factorization of 28 = 2 × 2 × 7
Prime factorization of 44 = 2 × 2 × 11
Prime factorization of 132 = 2 × 2 × 3 × 11
Here, 2 appears twice.
3, 7 and 11 appear once.
Therefore, the LCM of 28, 44 and 132 = 2 × 2 × 3 × 7 × 11 = 924
2. To find for instance, L.C.M. of 24, 36 and 40, we first factorise them completely.
24 = 2 × 2 × 2 × 3 = 2\(^{3}\) × 3\(^{1}\)
36 = 2 × 2 × 3 × 3 = 2\(^{2}\) × 3\(^{2}\)
40 = 2 × 2 × 2 × 5 = 2\(^{3}\) × 5\(^{1}\)
L.C.M. is the product of highest power of primes present in the factors.
Therefore, L.C.M. of 24, 36 and 40 = 2\(^{3}\) × 3\(^{2}\) × 5\(^{1}\) = 8 × 9 × 5 = 360
3. Find the L.C.M. of 8, 12, 16, 24 and 36
8 = 2 × 2 × 2 = 2\(^{3}\)
12 = 2 × 2 × 3 = 2\(^{2}\) × 3\(^{1}\)
16 = 2 × 2 × 2 × 2 = 2\(^{4}\)
24 = 2 × 2 × 2 × 3 = 2\(^{3}\) × 3\(^{1}\)
36 = 2 × 2 × 3 × 3 = 2\(^{2}\) × 3\(^{2}\)
Therefore, L.C.M. of 8, 12, 16, 24 and 36 = 2\(^{4}\) × 3\(^{2}\) = 144.
Method 1: Finding the LCM by Division Method:
Working Rules for Finding the LCM by Division Method:
Step I: Write all the given numbers in a line.
Step II: Think of the smallest prime number which is a factor of any of these numbers.
Step III: Divide all the numbers by this prime number obtained in step II. Remember that if any of these numbers is not divisible, retain it as it is.
Step IV: Repeat the steps II and III till you get all in the last row as 1.
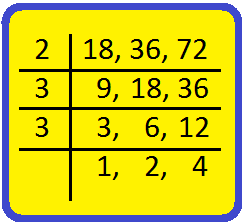
1. Find the LCM of 18, 36 and 72 by division method.
Solution:
Write the numbers in a row separated by commas. Divide the numbers by a common prime number. We stop dividing after reaching the prime number. Find the product of divisors and the remainders.
So, LCM of 18, 36 and 72 is 2 × 3 × 3 × 1 × 2 × 4 = 432.
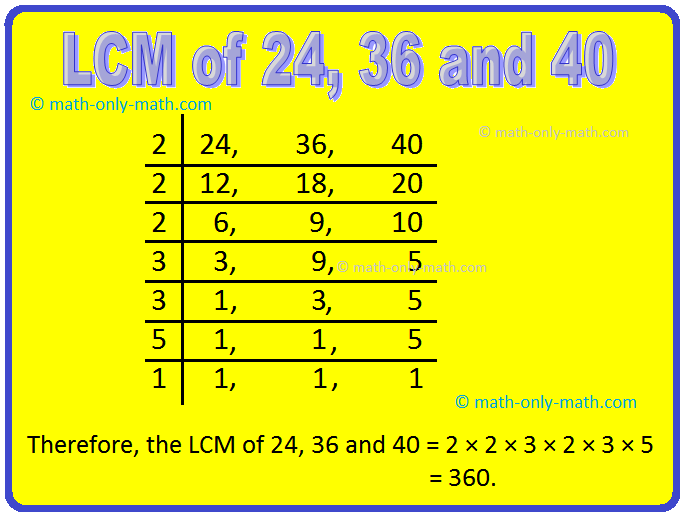
2. Find the LCM of 24, 36 and 40 by Division Method.
Solution:
Thus, LCM of 24, 36 and 40 =2 × 2 × 3 × 2 × 3 × 5 = 360.
LCM of Co-Prime Numbers:
LCM of the co-prime numbers is the product of the numbers.
For example:
1. Let us find the LCM of (4.9) and (3,5):
Therefore, the LCM of 4 and 9 = 4 × 9 = 36 and
the LCM of 3 and 5 = 3 × 5 = 15.
2. The LCM of two co-prime numbers is their
(a) sum; (b) difference; (c) product; (d) quotient
Solution:
It is obvious from above example that it is the product of numbers.
Therefore, the option (c) is correct.
Solved examples to find the lowest common multiple or the least common multiple:
1. Find the LCM of 3, 4 and 6 by listing the multiples.
Solution:
The multiple of 3 are 3, 6, 12, 15, 18, 21, 24
The multiple of 4 are 4, 8, 12, 16, 20, 24, 28
The multiple of 6 are 6, 12, 18, 24, 30, 36, 42
The common multiples of 3, 4 and 6 are 12 and 24
So, the least common multiple of 3, 4 and 6 is 12.
We can find LCM of given numbers by listing multiples or by long division method.
2. Find the first two common multiples of: 4 and 10
Solution:
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ......
Multiples of 10 are 10, 20, 30, 40......
Thus, the first two common multiples of 4 and 10 are 20 and 40.
Worksheet on Least Common Multiple:
I. Find the LCM of the given numbers. First one is shown for you as an example.
(i) 3 and 6
3 = 3, 6, 9, 12, 15, 18, 21, 24, 27 ………….
6 = 6, 12, 18, 24, 30, 36, 42 ………….
The common multiples of 3 and 6 are 6, 12, 18 ………….
Lowest common multiple of 3 and 6 is 6.
(ii) 2 and 4
(ii) 4 and 5
(iii) 3 and 12
(iv) 15 and 20
Answers:
I. (ii) 4
(ii20
(iii) 12
(iv) 60
You might like these
Even and Odd Numbers Between 1 and 100 | Even and Odd Numbers|Examples
All the even and odd numbers between 1 and 100 are discussed here. What are the even numbers from 1 to 100? The even numbers from 1 to 100 are:
5th Grade Factors and Multiples Worksheets | L.C.M. | H.C.F. | Answers
In 5th Grade Factors and Multiples Worksheets we will find the multiples of a given number, find the prime factors of a number, HCF of co-prime number, LCM of two co-prime numbers, HCF of two co-prime numbers, common multiples of three numbers, word problems on LCM and word
Worksheet on Divisibility Rules | Questions on Test of Divisibility
Worksheet on divisibility rules will help us to practice different types of questions on test of divisibility by 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11. We need to use the divisibility rules to find whether the given number is divisible by 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11.
Word Problems on H.C.F. and L.C.M. | Least Common Multiple | GCF Math
Here we will get the idea how to solve the word problems on H.C.F and L.C.M. 1. Find the smallest number which on adding 19 to it is exactly divisible by 28, 36 and 45. First we find the least
Worksheet on Word Problems on H.C.F. and L.C.M. |Highest Common Factor
In worksheet on word problems on H.C.F. and L.C.M. we will find the greatest common factor of two or more numbers and the least common multiple of two or more numbers and their word problems. I. Find the highest common factor and least common multiple of the following pairs
Relationship between H.C.F. and L.C.M. |Highest Common Factor|Examples
The product of highest common factor (H.C.F.) and lowest common multiple (L.C.M.) of two numbers is equal to the product of two numbers i.e., H.C.F. × L.C.M. = First number × Second number or, LCM × HCF = Product of two given numbers
Worksheet on L.C.M. | Least Common Multiple Worksheets |LCM Worksheets
Practice the questions given in the worksheet on l.c.m. to find the least common multiple by listing their multiples, by common prime factors and by division method. I. Find the L.C.M. of the following by listing their multiples. (i) 5, 10, 15 (ii) 4, 10, 12 (iii) 3, 9, 12
Multiples | Multiples of a Number |Common Multiple|First Ten Multiples
What are multiples? ‘The product obtained on multiplying two or more whole numbers is called a multiple of that number or the numbers being multiplied.’ We know that when two numbers are multiplied the result is called the product or the multiple of given numbers.
Worksheet on H.C.F. | Word Problems on H.C.F. | H.C.F. Worksheet | Ans
Practice the questions given in the worksheet on hcf (highest common factor) by factorization method, prime factorization method and division method. Find the common factors of the following numbers. (i) 6 and 8 (ii) 9 and 15 (iii) 16 and 18 (iv) 16 and 28
Highest Common Factor |Find the Highest Common Factor (H.C.F)|Examples
Highest common factor (H.C.F) of two or more numbers is the greatest number which divides each of them exactly. Now we will learn about the method of finding highest common factor (H.C.F). Steps 1: Find all the factors of each given number. Step 2: Find common factors of the
Worksheet on Methods of Prime Factorization |Prime Factors by Division
Practice the questions given in the worksheet on methods of prime factorization. 1. Each of the following is the prime factorization of a certain number. Find the number. (i) 2 × 5 × 7
Prime Factorisation |Complete Factorisation |Tree Factorisation Method
Prime factorisation or complete factorisation of the given number is to express a given number as a product of prime factor. When a number is expressed as the product of its prime factors, it is called prime factorization. For example, 6 = 2 × 3. So 2 and 3 are prime factors
Divisible by 9 | Test of Divisibility by 9 |Rules of Divisibility by 9
A number is divisible by 9, if the sum is a multiple of 9 or if the sum of its digits is divisible by 9. Consider the following numbers which are divisible by 9, using the test of divisibility by 9:
Divisible by 11|Test of Divisibility of 11|Rules of Divisibility by 11
A number is divisible by 11 if the sum of the digits in the odd places and the sum of the digits in the even places difference is a multiple of 11 or zero. To check whether a number is divisible by 11, we find the sum of the digits in the even places and the odd places
Divisible by 10|Test of Divisibility by 10|Rules of Divisibility by 10
Divisible by 10 is discussed below. A number is divisible by 10 if it has zero (0) in its units place. Consider the following numbers which are divisible by 10, using the test of divisibility by 10:
Common Multiples.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
From Least Common Multiple to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 01:32 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.