Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To Find Lowest Common Multiple by using Division Method
To find the LCM by division method, we write the given numbers in a row separately by commas, then divide the numbers by a common prime number. We stop dividing after reaching the prime numbers. The product of common and uncommon prime factor is the LCM of given numbers.
To find Least Common Multiple by using Division Method we need to follow the following steps.
Step 1: Write the given numbers in a horizontal line, separating them by commas.
Step 2: Divide them by a suitable prime number, which exactly divides at least two of the given numbers.
Step 3: We put the quotient directly under the numbers in the next row. If the number is not divided exactly, we bring it down in the next row.
Step 4: We continue the process of step 2 and step 3 until all co-prime numbers are left in the last row.
Step 5: We multiply all the prime numbers by which we have divided and the co-prime numbers left in the last row. This product is the least common multiple of the given numbers.
For Example:
1. Find least common multiple (L.C.M) of 20 and 30 by division method.
Solution:
Least common multiple (L.C.M) of 20 and 30 = 2 × 2 × 5 × 3 = 60.
2. Find least common multiple (L.C.M) of 50 and 75 by division method.
Solution:
Least common multiple (L.C.M) of 50 and 75 = 5× 5 × 2 × 3 = 150.
3. Find the LCM of 15, 35 and 45 using division method.
LCM of 15, 35 and 45 = 3 × 5 × 1 × 7 × 3 = 315.
4. Find the LCM of 18, 60 and 72 by division method.
Solution:
Therefore, LCM = 2 × 2 × 2 × 3 × 3 × 5 = 360.
Hence, the required LCM is 360.
Let us consider some of the examples to find lowest common multiple (L.C.M) of two or more numbers by using division method.
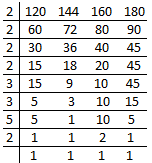
5. Find least common multiple (L.C.M) of 120, 144, 160 and 180 by using division method.
We can read the explanation and see below the L.C.M. of 120, 144, 160 and 180.
First we write all the numbers i.e. 120, 144, 160 and 180 in a row separating them by a dash or comma. Then we divide by a least prime number i.e. 2 which divides all the given numbers. Now we put the quotient i.e. 60, 72, 80 and 90 directly under the numbers in the next row.
Then again we divide by 2 and put the quotient i.e. 30, 36, 40 and 45 directly under the numbers in the next row.
We continue the process and similarly we divide by 2 and put the quotient i.e. 15, 18, 20 and 45. Here 45 will remain as it is because we can’t divide 45 by 2. So we directly write under the numbers in the next row.
Similarly again, we divide by 2 and put the quotient i.e. 15, 9, 10 and 45. Here 15 and 45 will remain as it is because we can’t divide 15 and 45 by 2 and we directly write under the numbers in the next row.
According to the explanation we continue the process and until all co-prime numbers are left in the last row.
And atlast we multiply all the prime numbers by which we have divided and the co-prime numbers left in the last row i.e. 2 × 2 × 2 × 2 × 3 × 3 × 5 × 2 = 1440.
Therefore, the product is the least common multiple of 120, 144, 160 and 180 is 1440.
6. Find the least number of four digits which leaves remainder 3 in each case when divided by 15, 18, 25 and 30.
Solucion:
First, find the LCM of the divisors.
Therefore, LCM of the given numbers = 2 × 3 × 3 × 5 × 5 = 450.
The smallest number of four digits is 1000.
The least number of 4 digits exactly divisible by the given divisors may be the multiple of 450 i.e., (450 × 3) = 1350
Hence, the required least 4-digit number is 1350 + 3 = 1353.
7. Determine the smallest natural number which when divided by 18, 35, 56 and 70 leaves remainder 7 in each case.
Solucion:
We know that the smallest natural number divisible by 18, 35, 56 and 70 is their LCM.
LCM of the given numiless = 2 × 2 × 2 × 3 × 3 × 5 × 7 = 2520.
The required number will be 7 more than their LCM.
Hence, the mind smallest natural number is 2520 + 7 = 2527.
8. Four bells toll at intervals of 3, 7, 12 and 14 seconds. If they begin to toll together at 5 pm, when will they next toll together?
Solution:
The time when all the four bells will toll together is the LCM of 3, 7, 12 and 14.
LCM of 3, 7, 12 and 14 = 2 × 2 × 3 × 7 = 84.
They will toll together after 54 seconds or 1 minute 24 seconds.
Hence, the required time will be 5:01:24 pm.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
From Lowest Common Multiple by using Division Method to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.