To find Least Common Multiple by using Prime Factorization Method
To find least common multiple by using prime factorization method is discussed here.
To find the LCM of two or more numbers, we first find all the prime factors of the given numbers and write them one below the other. Take one factor from each common group of factors and find their product. Multiply the product with other ungrouped factors. The resultant is the LCM of given numbers.
Step I:
Resolve each given number into its prime factors and express the factors obtained in exponent form.
Step I:
Find the product of the highest powers of all the factors that occur in any of the given numbers.
Step III:
The product obtained in Step II is the required least common multiple (L.C.M).
For example:
1. Find the least common multiple (L.C.M) of 9 and 15 by using prime factorization method.
Solution:
Step I:
Resolving each given number into its prime factors.
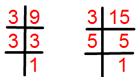
9 = 3 × 3 = 3².
15 = 3 × 5.
Step II:
The product of all the factors with highest powers.
= 3^2 × 5 = 3 × 3 × 5 = 45.
Step III:
The required least common multiple (L.C.M) of 9 and 15 = 45.
2. What is the least common multiple (L.C.M) of 16 and 28 by using prime factorization method?
Solution:
Step I:
Resolving each given number into its prime factors.
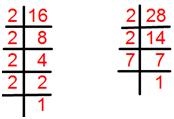
16 = 2 × 2 × 2 × 2 = 24.
28 = 2 × 2 × 7 = 22 × 7.
Step II:
The product of all the factors with highest powers.
= 24 × 7 = 2 × 2 × 2 × 2 ×7 = 112.
Step III:
The required least common multiple (L.C.M) of 16 and 28 = 112.
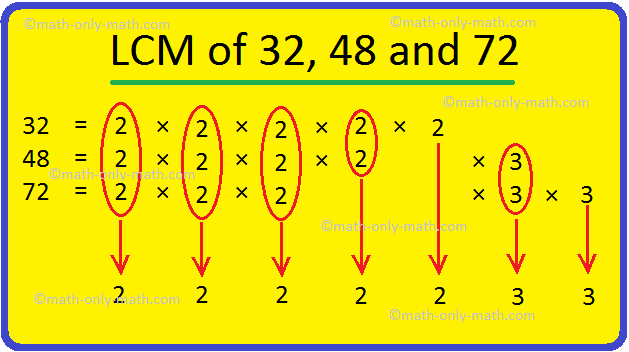
3. Find the LCM of 32, 48 and 72 by prime factorization.
Solution:
LCM of 32, 48 and 72 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288
Common Multiples.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
5th Grade Numbers Page
5th Grade Math Problems
From To find Least Common Multiple by using Prime Factorization Method to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Word Problems on Area and Perimeter | Free Worksheet with Answers
Jul 26, 24 04:58 PM
word problems on area and perimeter -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 26, 24 04:37 PM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Perimeter and Area of Irregular Figures | Solved Example Problems
Jul 26, 24 02:20 PM
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d… -
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
Jul 26, 24 11:50 AM
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles… -
5th Grade Math Problems | Table of Contents | Worksheets |Free Answers
Jul 26, 24 01:35 AM
In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.