5th Grade Test of Divisibility Rules

In 5th grade test of divisibility rules we will learn about the exact divisibility of a number by the numbers from 2 to 12.

Exact Divisibility by 2:

Verification: The digit in the ones place should be 2, 4, 6, 8 or 0.

For example: 752, 464, 356, 888, 990, etc.

Exact Divisibility by 3:

Verification: The sum of its digits should be exactly divisible by 3.

For example: 96, 513, 117, 972, 999, etc.

Exact Divisibility by 4:

Verification: The number, formed, by the last two digits of the number, should be a multiple of 4 or the last two digits should be 0.

For example: 124, 532, 648, 844, 1124,1300, etc.

Exact Divisibility by 5:

Verification: The digit in the ones place should be either 0 or 5.

For example: 40, 85, 115, 450, 885, 900, 1265, 3455, etc.

Exact Divisibility by 6:

Verification: The number should be exactly divisible by 2 and 3.

For example: 66, 90, 216, 576, 672, 1944, 3456, 32160, etc.

Exact Divisibility by 7:

Verification: The difference between double of the last digit and the number formed by the remaining digits of the number should be either 0 or multiple of 7.

For example: 84, 133, 224, 609, 777, 1680, 2492, 26292, etc.

Exact Divisibility by 8:

Verification: The last three digits should be exactly divisible by 8 or the last three digits should be 0.

For example: 896, 1024, 1192, 2392, 3648, 5000, 6976, etc.

Exact Divisibility by 9:

Verification: The sum of the digits should be a multiple of 9.

For example: 162, 225, 297, 351, 477, 594, 666, 783, 900, 999, etc.

Exact Divisibility by 10:

Verification: The last digit should be 0.

For example: 50, 90, 350, 730, 990, 3450, 67890, 456700 etc.

Exact Divisibility by 11:

Verification: Any number whose difference between the sum of digits at even places and odd places is 0 is exactly divisible by 11.

For example: 1353, 6237, 60170, 746790 etc.

Let us consider an example.

1. Verify whether 143 is exactly divisible by 11 or not.

Solution:

The digits at odd places are 1 and 3.

The digits at even place is 4.

The sum of the digits at odd places = 1 + 3 = 4.

The sum of the digits at even places = 4.

The difference between the sum of digits at odd and even places = 4 - 4 = 0

Therefore, 143 is exactly divisible by 11.

Exact Divisibility by 12:

Verification: The number, exactly divisible by 3 and 4 both, is exactly divisible by 12.

For example: 216, 300, 936, 2808 etc.

Let us consider an example.

1. Verify whether 2472 is exactly divisible by 12 or not.

Solution:

We can see that this number is exactly divisible by 3 as well as 4

(12472 ÷ 3 = 824;   2472 ÷ 4 = 6181)

So, 2472 is exactly divisible by 12.

We can conclude that the number, exactly divisible by 3 and 4 both, is exactly divisible by 12.

Solved Examples on 5th Grade Test of Divisibility Rules

Let us consider some examples of exact divisibility of different numbers by different numbers.

1. Verify whether 438 is exactly divisible by 4 or not.

Solution:

The last two digits of the given number form the number 38.

We see that 38 is not exactly divisible by 4 (38 ÷ 4 = 9 and remainder 2).

Therefore, the given number is not exactly divisible by 4.

2. Verify whether 4148 is exactly divisible by 8 or not.

Solution:

The number formed by the last three digits are 148.

We see that 148 is not exactly divisible by 8 (148 ÷ 8 = 18 and remainder 4).

Therefore, the given number is not exactly divisible by 8.

3. Verify whether 4833 is a multiple of 9 or not.

Solution:

The sum of the digits of the given number = 4 + 8 + 3 + 3 = 18

We see that 18 is exactly divisible by 9 (18 ÷ 9 = 2)

Therefore, the given number is exactly divisible by 9.

4. Verify whether 2468 is exactly divisible by 5 or not.

Solution:

We see that the last digit of the given number is neither 0 nor 5.

Therefore, the given number is not exactly divisible by 5.

5. Verify whether 1430 is exactly divisible by 11 or not.

Solution:

Sum of the digits at odd places = 1 + 3 = 4

Sum of the digits at even places = 4 + 0 = 4

We see that the difference between them is 4 - 4 = 0.

Therefore, 1430 is exactly divisible by 11.

6. Verify whether 1152 is exactly divisible by 12 or not.

Solution:

We see that 1152 is exactly divisible by 3 as well as 4 (1152 ÷ 3 = 384 and 1152 ÷ 4 = 288).

Therefore, the given number is exactly divisible by 12.

Worksheet on 5th Grade Test of Divisibility Rules

1. Complete the table using divisibility rules:

Answer:

1. 

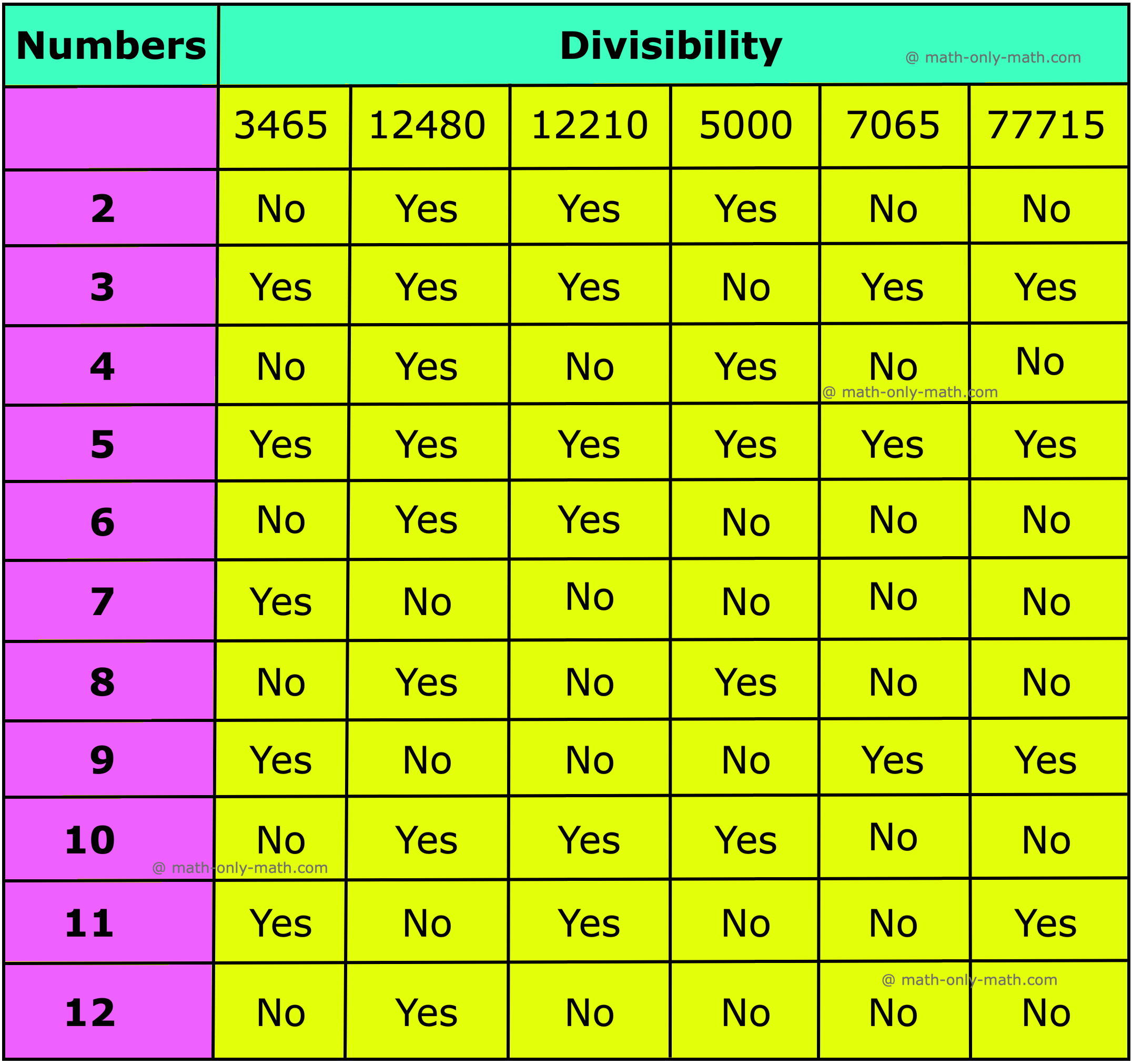
5th Grade Test of Divisibility Rules Answer

5th Grade Math Problems 

From 5th Grade Test of Divisibility Rules to HOME PAGE