Subtraction of Mass

In subtraction of mass we will learn how to find the difference between the units of mass or weight. While subtracting we need to follow that the units of mass i.e., kilogram and gram are converted into grams before subtraction and then follow the simple subtraction process.

We can subtract units of mass like ordinary numbers.

We will learn two different methods to solve subtraction using the standard unit and smaller unit of mass. Students can practice both the methods.

(i) Subtracting units with conversion into gram

(ii) Subtracting units without conversion into gram

Worked-out examples on subtraction of mass:

1. Subtract 11 kg 460 g from 25 kg 765 g

Solution:

Method I: (with conversion into gram):

We know, 1 kg = 1000 grams

Now kg and g are converted into grams before doing subtraction and then we need to follow the simple subtraction process.

11 kg 460 g = (11 × 1000) g + 460 g

                  = 11000 g + 460 g

                  = 11460 grams

25 kg 765 g = (25 × 1000) g + 765 g

                  = 25000 g + 765 g

                  = 25765 grams

Now sum,

             2 5 7 6 5  g

        -   1 1 4 6 0  g

             1 4 3 0 5  g

                     = 14 kg 305 g

Therefore, 25 kg 765 g - 11 kg 460 g = 11 kg 305 g 

Method II: (without conversion into gram):

Here kg and g are arranged in different columns and then added like ordinary numbers.

Follow the steps:

(i) kg and g are arranged in columns

(ii) 765 g - 460 g = 305 g

(iii) 25 kg - 11 kg = 14 kg

        kg       g

        25     765

    -   11     460

        14     305

              = 14 kg 305 g

Therefore, difference of 11 kg 460 g from 25 kg 765 g = 14 kg 305 g 

2. Subtract 24 kg 565 g from 45 kg 225 g

Solution:

Method I: (with conversion into gram):

We know, 1 kg = 1000 grams

Now kg and g are converted into grams before doing subtraction and then we need to follow the simple subtraction process.

24 kg 565 g = (24 × 1000) g + 565 g

                  = 24000 g + 565 g

                  = 24565 grams

45 kg 225 g = (45 × 1000) g + 225 g

                  = 45000 g + 225 g

                  = 45225 grams

Now sum,

             45225 g

          -  24565 g

             20660 g

                         = 20 kg 660 g

Therefore, 45 kg 225 g - 24 kg 565 g = 20 kg 660 g 

Method II: (without conversion into gram):

Here kg and g are arranged in different columns and then added like ordinary numbers.

Follow the steps:

(i) kg and g are arranged in columns

(ii) 225 g < 565 g, then 225 g - 565 g, so 1 kg from 45 kg is borrowed and added to 225 g

1 kg + 225 g = 1000 g + 225 g = 1225 g

1225 g - 565 g = 660 ml

(iii) 45 kg reduce into 44 kg

44 kg - 24 kg = 20 kg

        kg       g

        45     225

    -   24     565

        20     660

             = 20 kg 660 g

Therefore, difference of 24 kg 565 g from 45 kg 225 g = 20 kg 660 g 

3. Subtract  21 kg 370 g from 37 kg 675 g without conversion into gram.

Solution:

Here kg and g are arranged in different columns and then added like ordinary numbers (without conversion into gram).

        kg       g

        37     675

    -   21     370

        16     305

              = 16 kg 305 g

Therefore, difference of 21 kg 370 g from 37 kg 675 g = 16 kg 305 g 

4. Subtract 44 kg 900 g from 105 kg 60 g.

Solution:

Arrange the numbers vertically. First, subtract the grams. As 900 g > 60 g, we cannot subtract. We borrow 1 kg from 105 kg. So, 105 kg becomes 104 kg and 60 grams becomes 1000 + 60 = 1060 g. Subtract 900 g from 1060 g. 1060 – 900 = 160 Write 160 under grams column.

Subtract kilograms. 104 – 44 = 60 kg

Write 60 under kilograms column.

To subtract weights, write the number of kg and gin separate columns the subtract like ordinary numbers, starting from right.

5. Subtract 22 kg 70 g from 46 kg 90 g.

Solution:

              kg        g

             4 6      9 0

        -   2 2       7 0

            2 4       2 0

Answer: 24 kg 20 g

6. Subtract 682 kg 541 g from 325 kg 193 g.

Solution:

                 kg                g

                    7   12        4   13   11

             6   8   2       5   4   1

        -   3    2   5       1   9   3

            3    5   7       3   4   8

Answer: 357 kg 348 g

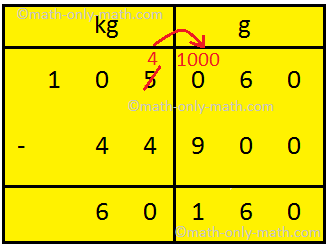
7. Subtract 30 kg 664 g from 65 kg 282 g

Solution:

30 kg 664 from 65 kg 282 g 65 kg 282 g - 30 kg 664 First subtract g here 282 < 664 So, we borrow 1 kg from 65 kg, leaving behind 64 kg. Also, 1 kg = 1000 g Thus, 65 kg 282 g becomes 64 kg 1282 g Subtract 664 from 1282. i.e., 1282 - 664 = 618 g Now subtract kg = (64 kg - 30 kg)                          = 34 kg

Therefore, the difference of the mass = 34 kg 618 g.

Subtraction of Weight

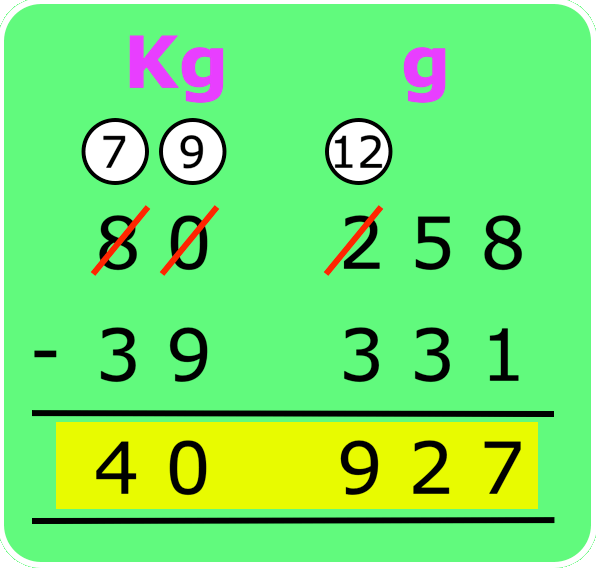
8. Subtract 39 kg 331 g from 80 kg 258 g.

Solution:

Step I: Write the weights to be subtracted in kg and g columns as shown.

Step II: Subtract the grams.

Step III: Subtract the kilograms.

Therefore, the answer is 40 kg 927 g.

SUBTRACTION OF KILOGRAMS AND GRAMS

Word Problems on Subtraction of Mass:

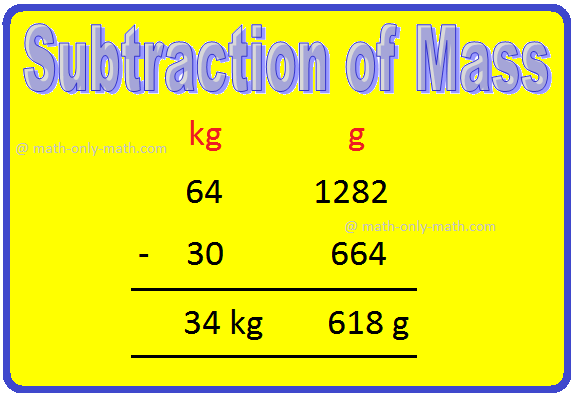
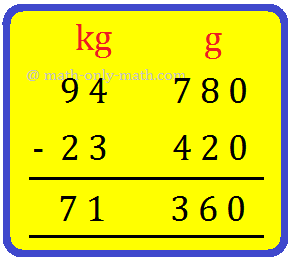
1. Anthony, the grocer, had 94 kilograms 780 grams of sugar. He sold 23 kilograms 420 grams of sugar in a week. How much sugar is left in his shop?

Solution:

Write kg and g in columns as shown.

Step I: Subtract g first. 780 - 420 = 360 Write 360 in the g column. Step II: Subtract kg now. 94 - 23 = 71 Write 71 in the kg column.

Therefore, the quantity of sugar left in the shop is 71 kg 360 g.

The above problems on subtraction of mass will help the students to practice the worksheet on subtracting the different units with conversion or without conversion.

Questions and Answers on Subtraction of Mass:

1. Subtract the given weights:

(i) 76 kg 142 g – 24 kg 031 g

(ii) 90 g 622 mg – 48 g 503 mg

(iii) 62 kg 579 g – 51 kg 560 g

(iv) 60 g 222 mg – 34 g 083 mg

(v) 80 kg 885 g – 47 kg 000 g

(vi) 100 kg 529 g – 36 kg 610 g

(vii) 27 g 021 mg – 9 g 300 mg

(viii) 321 kg 450 g – 50 kg 290 g

(ix) 560 kg 000 g – 110 kg 850 g

Answers:

1. (i) 52 kg 111 g

(ii) 42 g 119 mg

(iii) 11 kg 19 g

(iv) 26 g 139 mg

(v) 33 kg 885 g

(vi) 63 kg 919 g

(vii) 17 g 721 mg

(viii) 271 kg 160 g

(ix) 449 kg 150 g

2. Subtract the following:

Answer:

2. (i) 56 kg 30 g

(ii) 23 kg 20 g

(iii) 2 kg 44 g

(iv) 12 kg 37 g

(v) 33 kg 315 g

(vi) 35 kg 58 g

(vii) 14 kg 629 g

(viii) 98 kg 577 g 

(ix) 93 kg 825 g
 
(x) 194 kg 50 g

(xi) 112 kg 213 g

(xii) 236 kg 766 g

(xiii) 507 kg 965 g

(xiv) 20 kg 5 g

(xv) 408 kg 585 g

(xvi) 501 kg 938 g

● Related Concepts

● What is Mass?

● Conversion of Standard Unit of Mass

● Addition of Mass

3rd Grade Math Worksheets

3rd Grade Math Lessons

From Subtraction of Mass to HOME PAGE