Subtraction of Capacity

In subtraction of capacity we will learn how to find the difference between the units of capacity and volume. While subtracting we need to follow that the units of capacity i.e., liter and milliliter are converted into milliliters before subtraction and then follow the simple subtraction process.

We will learn two different methods to solve subtraction using the standard unit and smaller unit of capacity. Students can practice both the methods.

(i) Subtracting units with conversion into milliliter

(ii) Subtracting units without conversion into milliliter

We can subtract units of capacity measures just like ordinary numbers.

Worked-out examples on subtraction of capacity:

1. Subtract 6 l 250 ml from 15 l 500 ml

Solution:

Method I: (with conversion into milliliter):

We know, 1 liter = 1000 milliliters

Now liter and milliliter are converted into milliliters before doing subtraction and then we need to follow the simple subtraction process.

6 l 250 ml = (6 × 1000) ml + 250 ml = 6000 ml + 250 ml = 6250 milliliters

15 l 500 ml = (15 × 1000) ml + 500 ml = 15000 ml + 500 ml = 15500 milliliters

Now difference is, 

             15500 ml

          -   6250 ml

              9250 ml

                         = 9 l 250 ml

Therefore, 15 l 500 ml - 6 l 250 ml = 9 l 250 ml

Method II: (without conversion into milliliter):

Here liter and milliliter are arranged in different columns and then subtract like ordinary numbers.

Follow the steps:

(i) Liter and milliliter are arranged in columns

(ii) 500 ml - 250 ml = 250 ml

(iii) 15 l - 6 l = 9 l

              l       ml
            15     500

        -    6     250

             9     250

                        = 9 l 250 ml

Therefore, difference of 6 l 250 ml from 15 l 500 ml = 9 l 250 ml 

2. Subtract 6 l 650 ml from 18 l 875 ml

Solution:

Method I: (with conversion into milliliter):

We know, 1 liter = 1000 milliliters

Now liter and milliliter are converted into milliliters before doing subtraction and then we need to follow the simple subtraction process.

6 l 650 ml = (6 × 1000) ml + 650 ml = 6000 ml + 650 ml = 6650 milliliters

18 l 875 ml = (18 × 1000) ml + 875 ml = 18000 ml + 875 ml = 18875 milliliters

Now difference is,

                      1 8 8 7 5 ml

                  -     6 6 5 0 ml

                      1 2 2 2 5 ml

                                = 12 l 225 ml

Therefore, 18 l 875 ml - 6 l 650 ml = 12 l 225 m

Method II: (without conversion into milliliter):

Here liter and milliliter are arranged in different columns and then subtract like ordinary numbers.

Follow the steps:

(i) Liter and milliliter are arranged in columns

(ii) 875 ml - 650 ml = 225 ml

(iii) 18 l - 6 l = 12 l

                  l       ml
                18     875

             -    6     650

                 12     225

                            = 12 l 225 ml

Therefore, difference of 6 l 650 ml from 18 l 875 ml = 12 l 225 ml 

More solved examples on subtraction of capacity where the method is mentioned in the given question.

3. Subtract 7 l 850 ml from 19 l 375 ml without conversion into milliliter.

Solution:

Without conversion into milliliter here liter and milliliter are arranged in different columns and then subtract like ordinary numbers.

Follow the steps:

(i) Liter and milliliter are arranged in columns

(ii) 850 ml - 375 ml, so 1 l from 19 l is borrowed and added to 375 ml

1 l + 375 ml = 1375 ml

1375 ml - 850 ml = 525 ml

(iii) 19 l reduce into 18 l

18 l - 7 l = 11 l

                  l        ml
                     1      1000
                19      375

             -    7      850
                11      525

                             = 11 l 525 ml

Therefore, difference of 7 l 850 ml from 19 l 375 ml = 11 l 525 ml 

4. Subtract 4 l 250 ml from 13 l 750 ml with conversion into milliliter.

Solution:

With conversion into milliliter we will do simple subtraction.

We know, 1 liter = 1000 milliliters

Now liter and milliliter are converted into milliliters before doing subtraction and then we need to follow the simple subtraction process.

4 l 250 ml = (4 × 1000) ml + 250 ml = 4000 ml + 250 ml = 4250 milliliters

13 l 750 ml = (13 × 1000) ml + 750 ml = 13000 ml + 750 ml = 13750 milliliters

Now difference is, 

                13750 ml

             -   4250 ml

                 9500 ml

                             = 9 l 500 ml

Therefore, 13 l 750 ml - 4 l 250 ml = 9 l 500 ml

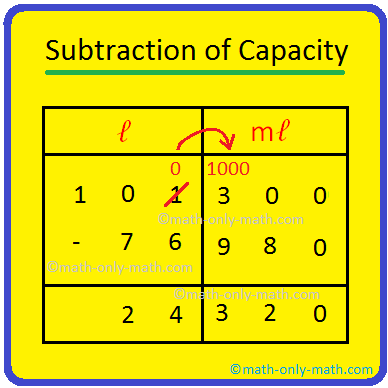
5. Subtract 76 l 980 ml from 101 l 300 ml.

Solution:

Arrange the numbers vertically. First subtract the ml Since, 980 ml > 300 ml, we cannot subtract. We borrow 1 l and subtract 980 from 1300. 1300 – 980 = 320 ml, write 320 under ml column. Subtract liters. 100 – 76 = 24 l Write 24 under liters column.

Hence, 101 l 300 ml – 76 l 980 ml = 24 l 320 ml

To subtract, write the number of mℓ and ℓ in separate columns then subtract like ordinary numbers starting from the right.

6. Subtract 22 ℓ 20 mℓ from 45 ℓ 60 mℓ.

               ℓ      mℓ

             45     60

         -  22      20

             23     40

Answer: 23 ℓ 40 mℓ

7. Subtract 268 ℓ 994 mℓ from 866 ℓ 793 mℓ.

                     ℓ              mℓ

                   7   15  15       16  18  13

               8   6   6      7   9   3

           -  2   6   8       9   9   4

         ___5   9   7      7   9    9

Answer: 597 ℓ 799 mℓ

8. Find the difference of the capacity: 15 ℓ 624 mℓ from 43 ℓ 312 mℓ.

Solution:

15 ℓ 624 mℓ from 43 ℓ 312 mℓ 43 ℓ 312 mℓ - 15 ℓ 624 mℓ First subtract mℓ; but 312 < 624 So, we borrow 1 ℓ from 43 ℓ, leaving behind 42 ℓ Thus, 43 ℓ 312 mℓ becomes 42 ℓ 1312 mℓ Subtract 624 from 1312 i.e., 1312 -624 = 688 ml Now, subtract   = (42 ℓ - 15 ℓ) = 27 ℓ

Required difference of the capacity = 27 ℓ 688 mℓ

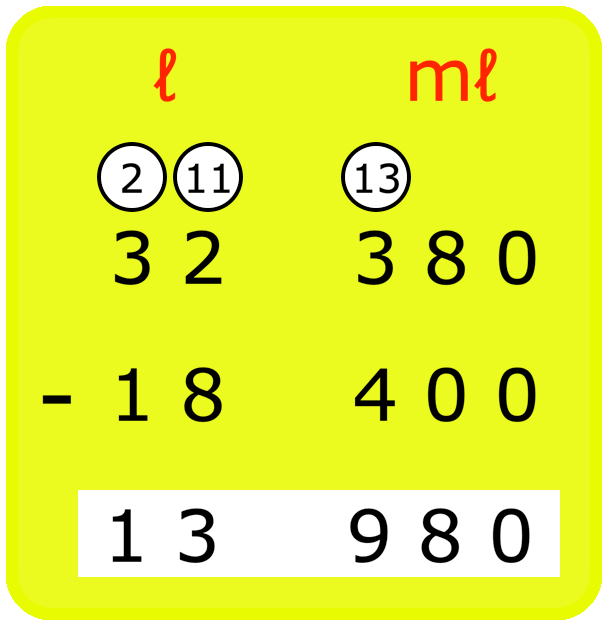
9. Subtract 18 l 400 ml from 32 l 380 ml.

Solution:

Step I: Write the volumes to be subtracted in l and ml columns as shown.

Step II: Subtract the millilitres.

Step III: Then subtract the litres.

Therefore, the answer is 13 l 980 ml

Word problems on subtraction of capacity and volume:

SUBTRACTION OF LITRES AND MILLILITRES

10. Olivia purchased 7 l 500 ml of milk. She consumed 3 l 700 ml of milk during the day. How much milk was left? 

Solution:

Quantity of milk purchased                         =             7 l 500 ml

Quantity of milk consumed                         =             3 l 700 ml

Therefore, quantity of milk left                   =             3 l 800 ml

11. Anthony, the milkman, has 28 litres 500 millilitres of milk in his can. He gave 15 litres 300 millilitres to Donald, the shopkeeper. How much milk is left in his can now?

Write and me in columns as shown.

Step I: Subtract mℓ first.   500 - 300 = 200   Write 200 in the mℓ column.   Step II: Subtract ℓ now.   28 - 15 = 13   Write 13 in the ℓ column.

Therefore, the milk left in the can is 13 ℓ 200 mℓ.

The above problems on subtraction of capacity and volume will help the students to practice the worksheet on subtracting the different units with conversion or without conversion.

Worksheet on Subtraction of Capacity:

I. Subtract the following:

(i) 24 l 445 ml – 14 l 134 ml

(ii) 65 l 109 ml – 42 l 813 ml

(iii) 74 l 340 ml – 51 l 250 ml

(iv) 90 l 000 ml – 42 l 056 ml

(v) 81 l 550 ml - 62 l 125 ml

(vi) 72 l 160 ml – 54 l 320 ml

Answers:

I. (i) 10 l 311 ml

(ii) 22 l 296 ml

(iii) 23 l 90 ml

(iv) 47 l 944 ml

(v) 19 l 425 ml

(vi) 17 l 840 ml

II. Subtract the following:

Answer:

II. (i) 32 ℓ 15 mℓ

(ii) 31 ℓ 8 mℓ

(iii) 14 ℓ 32 mℓ

(iv) 21 ℓ 61 mℓ

(v) 33 ℓ 25 mℓ

(vi) 11 ℓ 31 mℓ

(vii) 21 ℓ 52 mℓ

(viii) 54 ℓ 22 mℓ

(ix) 106 ℓ 225 mℓ
 
(x) 243 ℓ 864 mℓ

(xi) 220 ℓ 259 mℓ

(xii) 200 ℓ 179 mℓ

(xiii) 294 ℓ 808 mℓ

(xiv) 243 ℓ 864 mℓ

(xv) 101 ℓ 3 mℓ

(xvi) 180 ℓ 923 mℓ

● Related Concepts

● Standard Unit of Capacity

● Conversion of Standard Unit of Capacity

● Addition of Capacity

3rd Grade Math Worksheets

3rd Grade Math Lessons

From Subtraction of Capacity to HOME PAGE