Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition of Capacity
In addition of capacity we will learn how to add the different units of capacity and volume together. While adding we need to follow that the units of capacity i.e., liter and milliliter are converted into milliliters before addition and then follow the simple addition process.
We will learn two different methods to solve addition using the standard unit and smaller unit of capacity. Students can practice both the methods.
(i) Adding units with conversion into milliliters
(ii) Adding units without conversion into milliliters
We can add two or more units of capacity ℓ and mℓ just like ordinary numbers.
Worked-out Examples on Addition of Capacity and Volume:
1. Add 3 ℓ 600 mℓ and 6 ℓ 300 mℓ
Solution:
Method I: (with conversion into milliliters):
We know, 1 liter = 1000 milliliters
Now liter (ℓ) and milliliters (mℓ) are converted into mℓ before doing addition and then we need to follow the simple addition process.
3 ℓ 600 mℓ = (3 × 1000) mℓ + 600 mℓ
= 3000 mℓ + 600 mℓ
= 3600 milliliters
6 ℓ 300 mℓ = (6 × 1000) mℓ + 300 mℓ
= 6000 mℓ + 300 mℓ
= 6300 milliliters
Now sum,
3600 mℓ
+ 6300 mℓ
9900 mℓ
= 9 ℓ 900 mℓ
Therefore, 3 ℓ 600 mℓ + 6 ℓ 300 mℓ = 9 ℓ 900 mℓ.
Method II: (without conversion into milliliters):
Here ℓ and mℓ are arranged in different columns and then added like ordinary numbers.
(i) ℓ and mℓ are arranged column-wise
(ii) 600 mℓ + 300 mℓ = 900 mℓ
(iii) 3 ℓ + 6 ℓ = 9 ℓ
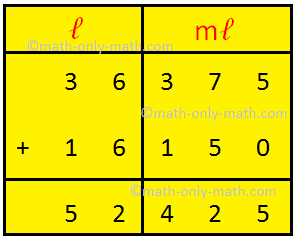
ℓ mℓ
3 600
+ 6 300
9 900
= 9 ℓ 900 mℓ
Therefore, sum of 3 ℓ 600 mℓ and 6 ℓ 300 mℓ = 9 ℓ 900 mℓ.
2. Add 5 ℓ 725 mℓ and 8 ℓ 450 mℓ
Solution:
Method I: (with conversion into milliliters):
We know, 1 liter = 1000 milliliters
Now liter (ℓ) and milliliters (mℓ) are converted into ml before doing addition and then we need to follow the simple addition process.
5 ℓ 725 mℓ = (5 × 1000) mℓ + 725 mℓ
= 5000 mℓ + 725 mℓ
= 5725 milliliters
8 ℓ 450 mℓ = (8 × 1000) mℓ + 450 mℓ
= 8000 mℓ + 450 mℓ
= 8450 milliliters
Now sum,
1
5725 mℓ
+ 8450 mℓ
14175 mℓ
= 14 ℓ 175 mℓ
Therefore, 5 ℓ 725 mℓ + 8 ℓ 450 mℓ = 14 ℓ 175 mℓ
Method II: (without conversion into milliliters):
Here ℓ and mℓ are arranged in different columns and then added like ordinary numbers.
(i) ℓ and mℓ are arranged column-wise
(ii) 725 mℓ + 450 mℓ = 1 ℓ 175 mℓ.
175 mℓ is placed under mℓ. 1 ℓ is taken in ℓ column.
(iii) 1 ℓ + 5 ℓ + 8 ℓ = 14 ℓ
ℓ mℓ
1
5 725
+ 8 450
14 175
= 14 ℓ 175 mℓ
Therefore, sum of 5 ℓ 725 mℓ and 8 ℓ 450 mℓ = 14 ℓ 175 mℓ.
More solved examples on addition of capacity where the method is mentioned in the given question.
3. Add 17 ℓ 387 mℓ, 7 ℓ 750 mℓ and 9 ℓ without conversion into milliliters.
Solution:
Without conversion into milliliters here ℓ and mℓ are arranged in different columns and then added like ordinary numbers.
(i) ℓ and mℓ are arranged column-wise
(ii) 387 mℓ + 750 mℓ = 1 ℓ 137 mℓ.
137 mℓ is placed under mℓ. 1 ℓ is taken in ℓ column.
(iii) 1 ℓ + 17 ℓ + 7 ℓ + 9 ℓ = 34 ℓ
ℓ mℓ
21 1
17 387
7 750
+ 9 000
34 137
= 34 ℓ 137 mℓ
Therefore, sum of 17 ℓ 387 mℓ, 7 ℓ 750 mℓ and 9 ℓ = 34 ℓ 137 mℓ.
4. Add 13 ℓ 250 mℓ, 8 ℓ 750 mℓ and 6 ℓ with conversion into milliliters
Solution:
With conversion into milliliters here we will do the addition process.
We know, 1 liter = 1000 milliliters
Now liter (ℓ) and milliliters (mℓ) are converted into ml before doing addition and then we need to follow the simple addition process.
13 ℓ 250 mℓ = (13 × 1000) mℓ + 250 mℓ
= 13000 mℓ + 250 mℓ
= 13250 milliliters
8 ℓ 750 mℓ = (8 × 1000) mℓ + 750 mℓ
= 8000 mℓ + 750 mℓ
= 8750 milliliters
6 ℓ = (6 × 1000) mℓ
= 6000 milliliters
Now sum,
111
13250 mℓ
8750 mℓ
+ 6000 mℓ
28000 mℓ
= 28 ℓ 000 mℓ
= 28000 mℓ
Therefore, 13 ℓ 250 mℓ + 8 ℓ 750 mℓ + 6 ℓ = 28000 mℓ
5. Add 36 ℓ 275 mℓ and 16 ℓ 150 mℓ.
|
Solution: Arrange the numbers vertically. First, add the milliliters. 275 mℓ + 150 mℓ = 425 mℓ Add the liters 36 ℓ + 16 ℓ = 52 ℓ |
Hence, 36 ℓ 275 mℓ + 16 ℓ 150 mℓ = 52 ℓ 425 mℓ
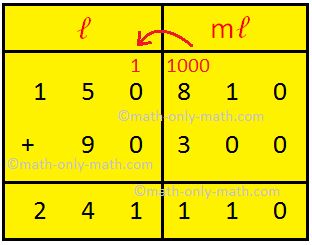
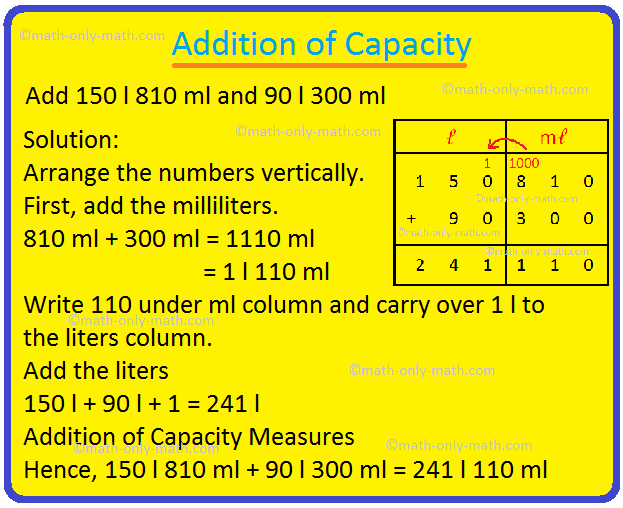
6. Add 150 ℓ 810 mℓ and 90 ℓ 300 mℓ
Solution:
|
Arrange the numbers vertically. First, add the milliliters. 810 mℓ + 300 mℓ = 1110 mℓ = 1 ℓ 110 mℓ Write 110 under mℓ column and carry over 1 ℓ to the liters column. Add the liters 150 ℓ + 90 ℓ + 1 = 241 ℓ |
Hence, 150 ℓ 810 mℓ + 90 ℓ 300 mℓ = 241 ℓl 110 mℓ
For addition, write the number of mℓ and ℓ in separate columns then add like ordinary numbers. starting from the right.
7. Add 27 ℓ 450 mℓ & 52 ℓ 120 mℓ.
Solution:
mℓ ℓ
27 450
+ 52 120
79 570
Answer: 79 mℓ 570 mℓ
8. Add 214 ℓ 321 mℓ, 426 ℓ 932 mℓ & 358 ℓ 416 mℓ.
Solution:
mℓ ℓ
1 1
2 1 4 3 2 1
4 2 6 9 3 2
+ 3 5 8 4 1 6
9 9 9 6 6 9
Answer: 999 mℓ 669 mℓ
9. Find the sum of the capacity: 28 ℓ 32 mℓ + 73 ℓ 68 mℓ
|
Solution: 28 ℓ 32 mℓ + 73 ℓ 68 mℓ First add mℓ = 32 mℓ + 68 mℓ = 100 mℓ Now add liters = 28 ℓ + 93 ℓ = 121 ℓ |
Therefore, required sum = 121 ℓ 100 mℓ
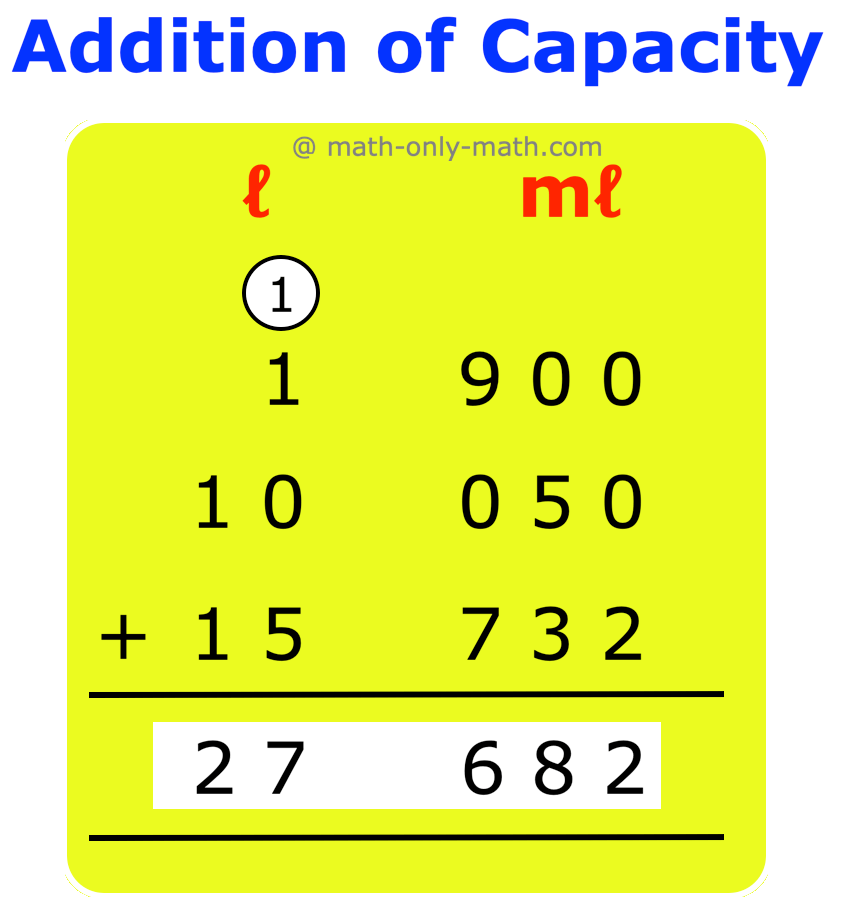
10. Find the sum of the capacities 1 ℓ 900 mℓ, 10 ℓ 50 mℓ and 15 ℓ 732 mℓ.
Solution:
Step I: Write the volumes to be added in ℓ and mℓ columns as shown.
Step II: Add the millilitres.
Step III: Then add the litres.
Remember to add the carry overs.
Therefore, the answer is 27 ℓ 682 mℓ.
Word Problems on Addition of Capacity and Volume:
ADDITION OF LITRES AND MILLILITRES
11. Finn purchased 3 ℓ 250 mℓ of milk on Monday, 2 ℓ 750 mℓ on Wednesday and 3 ℓ 500 mℓ on Friday. How much milk did Finn purchased during these three days?
Solution:
1 1
Milk purchased on Monday = 3 ℓ 250 mℓ
Milk purchased on Wednesday = 2 ℓ 750 mℓ
Milk purchased on Friday = 3 ℓ 500 mℓ
+
Therefore, total milk purchased during these 3 days = 9 ℓ 500 mℓ
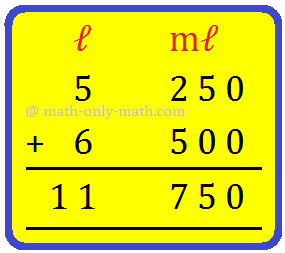
12. Nisha poured 5 litres 250 millilitres of water in a bucket. Tanya poured 6 litres 500 millilitres of water in the same bucket. How much water is there in the bucket now?
Solution:
Write ℓ and mℓ in columns as shown.
|
Step I: Add mℓ first. 250 + 500 = 750 Write 750 in the mℓ column. Step II: Add ℓ now. 5 + 6 = 11 Write 11 in the ℓ column. |
Therefore, the total quantity of water in the bucket is 11 ℓ 750 mℓ.
The above problems on addition of capacity will help the students to practice the worksheet on adding the different units with conversion or without conversion.
Worksheet on Addition of Capacity:
I. Add the following:
(i) 7 ℓ 152 mℓ + 2 ℓ 339 mℓ
(ii) 5 ℓ 240 mℓ + 7 ℓ 860 mℓ
(iii) 70 ℓ 000 mℓ + 22 ℓ 504 mℓ
(iv) 13 ℓ 1290 mℓ + 18 ℓ 160 mℓ
(v) 32 ℓ 540 mℓ + 18 ℓ + 210 mℓ
(vi) 19 ℓ 300 mℓ + 3 ℓ 900 mℓ
(vii) 62 ℓ 200 mℓ + 15 mℓ 385 mℓ
(viii) 120 ℓ + 625 mℓ + 30 ℓ 750 mℓ
(ix) 21 ℓ 845 mℓ + 32 ℓ 116 mℓ + 38 ℓ 082 mℓ
Answers:
I. (i) 9 l 491 ml
(ii) 13 l 100 ml
(iii) 92 l 504 ml
(iv) 31 l 450 ml
(v) 50 l 750 ml
(vi) 23 l 200 ml
(vii) 77 l 585 ml
(viii) 151 l 375 ml
(ix) 92 l 43 ml
II. Add the following:
|
(i) |
mℓ ℓ 21 27 + 48 32 _ _______ _ |
(ii) |
mℓ ℓ 86 45 + 12 20 _ _______ _ |
|
(iii) |
mℓ ℓ 27 10 + 11 25 _ _______ _ |
(iv) |
mℓ ℓ 32 94 + 60 05 _ _______ _ |
|
(v) |
mℓ ℓ 17 826 + 23 578 _ _______ __ |
(vi) |
mℓ ℓ 46 950 + 39 475 _ ________ _ |
|
(vii) |
mℓ ℓ 76 586 + 45 674 _ _______ __ |
(viii) |
mℓ ℓ 51 700 + 48 300 _ ________ _ |
|
(ix) |
mℓ ℓ 209 68 214 09 + 116 00 _ _______ __ |
(x) |
mℓ ℓ 423 00 147 05 + 208 79 _ _______ __ |
|
(xi) |
mℓ ℓ 126 90 103 70 + 264 50 _ _______ __ |
(xii) |
mℓ ℓ 210 73 216 08 + 205 98 _ _______ __ |
|
(xiii) |
mℓ ℓ 205 853 369 786 + 8 678 _ ________ __ |
(xiv) |
mℓ ℓ 125 675 465 850 + 310 625 _ ________ __ |
|
(xv) |
mℓ ℓ 318 564 237 658 + 8 678 _ ________ __ |
(xvi) |
mℓ ℓ 275 750 117 650 + 10 545 _ ________ __ |
Answer:
2. (i) 69 ℓ 59 mℓ
(ii) 98 ℓ 65 mℓ
(iii) 38 ℓ 35 mℓ
(iv) 92 ℓ 99 mℓ
(v) 41 ℓ 404 mℓ
(vi) 86 ℓ 425 mℓ
(vii) 122 ℓ 260 mℓ
(viii) 100 ℓ 00 mℓ
(ix) 53 ℓ 977 mℓ
(x) 77 ℓ 884 mℓ
(xi) 49 ℓ 510 mℓ
(xii) 63 ℓ 279 mℓ
(xiii) 584 ℓ 317 mℓ
(xiv) 902 ℓ 150 mℓ
(xv) 564 ℓ 600 mℓ
(xvi) 403 ℓ 945 mℓ
● Related Concepts
● Conversion of Standard Unit of Capacity
From Addition of Capacity to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.