Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition of Mass
In addition of mass we will learn how to add the different units of mass or weight together.
Let us learn how to add different units of mass.
While adding we need to follow that the units of mass i.e., kilogram and gram are converted into grams before addition and then follow the simple addition process. We can add two or more units of mass given in kilogram and grams like ordinary numbers. Always express grams as 3-digit numbers for example 3 g = 003 g.
We will learn two different methods to solve addition using the standard unit and smaller unit of mass. Students can practice both the methods.
(i) Adding units with conversion into gram
(ii) Adding units without conversion into gram
Worked-out examples on addition of mass:
1. Add 7 kg 350 g and 2 kg 150 g
Solution:
Method 1 (with conversion into gram):
We know, 1 kg = 1000 grams
Now kg and g are converted into grams before doing addition and then we need to follow the simple addition process.
7 kg 350 g = (7 × 1000) g + 350 g
= 7000 g + 350 g
= 7350 grams
2 kg 150 g = (2 × 1000) g + 150 g
= 2000 g + 150 g
= 2150 grams
Now sum,
1
7 3 5 0 g
+ 2 1 5 0 g
9 5 0 0 g
= 9 kg 500 g
Therefore, 7 kg 350 g + 2 kg 150 g = 9 kg 500 g
Method 2 (without conversion into gram):
Here kg and g are arranged in different columns and then added like ordinary numbers.
kg g
1
7 3 5 0
+ 2 1 5 0
9 5 0 0
= 9 kg 500 g
Therefore, sum of 7 kg 350 g and 2 kg 150 g = 9 kg 500 g
2. Add 8 kg 575 g and 4 kg 897 g
Solution:
Method 1 (with conversion into gram):
We know, 1 kg = 1000 grams
Now kg and g are converted into grams before doing addition and then we need to follow the simple addition process.
8 kg 575 g = (8 × 1000) g + 575 g
= 8000 g + 575 g
= 8575 grams
4 kg 897 g = (4 × 1000) g + 897 g
= 4000 g + 897 g
= 4897 grams
Now sum,
1 1 1
8 5 7 5 g
+ 4 8 9 7 g
1 3 4 7 2 g
= 13 kg 472 g
Therefore, 8 kg 575 g + 4 kg 897 g = 13 kg 472 g
Method 2 (without conversion into gram):
Here kg and g are arranged in different columns and then added like ordinary numbers.
kg g
1 1 1
8 5 7 5
+ 4 8 9 7
1 3 4 7 2
= 13 kg 472 g
Therefore, sum of 8 kg 575 g and 4 kg 897 g = 13 kg 472 g
3. Add 17 kg, 13 kg 940 g and 15 kg 65 g
Solution:
Here kg and g are arranged in different columns and then added like ordinary numbers (without conversion into gram).
kg g
11 1
17 000
13 940
+ 15 065
46 005
= 46 kg 005 g
Therefore, sum of 17 kg, 13 kg 940 g and 15 kg 65 g = 46 kg 005 g
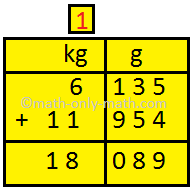
4. Add 6 kg 135 g and 11 kg 954 g.
Solution:
|
Arrange the numbers vertically. First, add the grams. 135 + 954 = 1089 g = 1000 g + 89 g Write 89 under grams column and carry over 1 kg to kilograms column. Add the kilograms. 6 + 11 + 1 (carry over) = 18 kg |
Write 18 kg under the kilograms column.
Hence, 6 kg 135 g + 11 kg 954 g = 18 kg 89 g.
5. Add: 45 kg 726 g, 23 kg 12 g and 7 kg 53 g.
|
Solution: Let us add Step I: Arrange the numbers vertically. Step II: Write the weights to be added in kg and g as shown here. Step III: First add grams from right and then add the kilograms. |
Thus, 45 kg 726 g + 23 kg 12 g + 7 kg 53 g = 75 kg 791 g
To add weight, write the number of kg and g in separate columns then add like ordinary numbers, starting from the right.
6. Add 28 kg 460 g + 45 kg 385 g.
Solution:
kg g
1 1
2 8 4 6 0
+ 4 5 3 8 5
7 3 8 4 5
Answer: 73 kg 845 g
7. Add 43 kg 56 g, 12 kg 74 g & 21 kg 95 g.
kg g
2 1
4 3 5 6
1 2 7 4
+ 2 1 9 5
7 8 2 5
Answer: 78 kg 25 g
8. Find the sum of the weight 19 kg 400 g + 17 kg 700 g:
|
Solution: 19 kg 400 g + 17 kg 700 g First add g = 400 g + 700 g = 1100 g = 1 kg 100 g Now add kg = 19 kg + 17 kg + 1 kg (carry) = 37 kg |
Therefore, the required sum of the weight = 37 kg 100 g
Addition of Weight
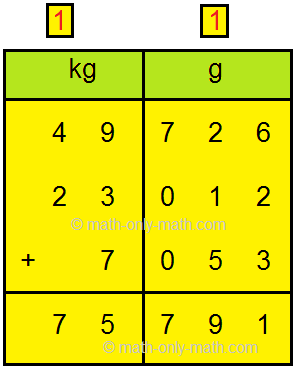
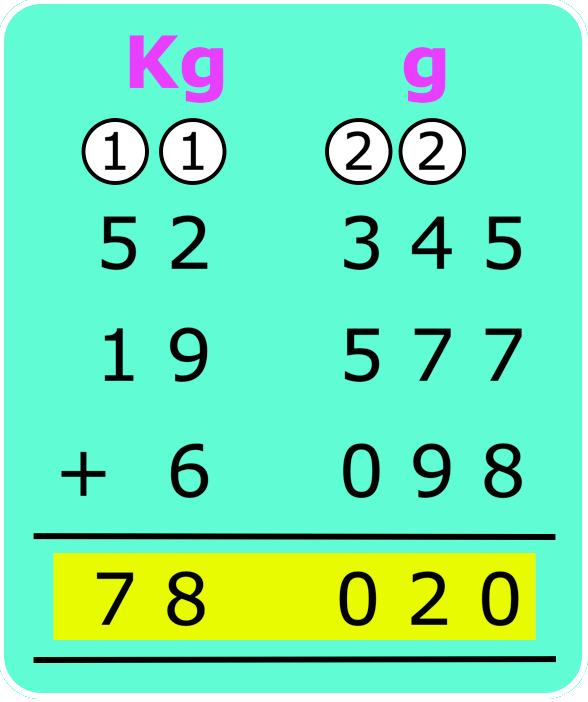
9. Add 52 kg 345 g, 19 kg 577 g and 6 kg 98g.
Solution:
Step I:
Write the weights to be added in kg and g columns as shown.
Step II:
Add the grams.
Step III:
Then add the kilograms. Remember to add the carry overs.
Therefore, the answer is 78 kg 20 g.
ADDITION OF KILOGRAMS AND GRAMS
Word Problems on Addition of Mass
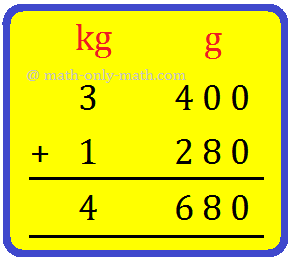
1. Robert is carrying a bag whose weight is 3 kilograms 400 grams. He puts a packet weighing 1 kilogram 280 grams in the bag. What is the weight of the bag now?
Solution:
Write kg and g in columns as shown.
|
Step I: Add g first. 400 + 280 = 680 Write 680 in the g column. Step II: Add kg now. 3 + 1 = 4 Write 4 in the kg column. |
Therefore, the total weight of the bag is 4 kg 680 g.
The above problems on addition of mass will help the students to practice the worksheet on adding the different units with conversion or without conversion.
Worksheet on Addition of Weight:
I. Add the given weights:
(i) 23 kg 084 g + 16 kg 214 g
(ii) 32 g 132 mg + 57 g 265 mg
(iii) 34 kg 000 g + 19 kg 075 g
(iv) 44 kg 725 g + 15 kg 200 g
(v) 70 kg 600 g + 18 kg 504 g
(vi) 41 g 800 mg + 12 g 200 mg + 33 g 082 mg
Answers:
I. (i) 39 kg 298 g
(ii) 89 g 397 mg
(iii) 53 kg 75 g
(iv) 59 kg 925 g
(v) 89 kg 104 g
(vi) 87 g 82 mg
II. Add the following:
(i) 23 kg 673 g, 10 kg 98 g and 5 kg 600 g
(ii) 38 kg 900 g, 17 kg 547 g and 12 kg 621 g
(iii) 56 kg 411 g, 21 kg 561 g and 8 kg
(iv) 156 kg 32 g, 441 kg 198 g and 158 kg 200 g
(v) 200 kg 500 g, 279 kg 679 g and 134 kg 450 g
(vi) 250 kg 60 g, 45 kg 100 g and 90 kg 300 g
(vii) 180 kg 110 g, 170 kg 85 g and 60 kg 50 g
(viii) 310 kg 500 g, 105 kg 180 g and 15 kg 50 g
(ix) 75 kg 350 g, 150 kg 200 g and 225 kg 175 g
Answer:
II. (i) 39 kg 371 g
(ii) 69 kg 68 g
(iii) 85 kg 972 g
(iv) 755 kg 43 g
(v) 614 kg 629 g
(vi) 385 kg 460 g
(vii) 410 kg 245 g
(viii) 430 kg 730 g
(ix) 450 kg 725 g
III. Add the following:
(i) 23 kg 345 g, 12 kg 120 g and 5 kg 78 g
(ii) 127 kg 437 g, 67 kg 790 g and 34 kg
(iii) 904 kg 230 g, 14 kg 780 g and 17 kg 495 g
(iv) 33 kg 480 g, 348 kg 560 g and 70 kg 30 g
(v) 65 kg 632 g, 121 kg 12 g and 130 kg
Answer:
III. (i) 405 kg 543 g
(ii) 229 kg 227 g
(iii) 936 kg 505 g
(iv) 452 kg 70 g
(v) 316 kg 644 g
IV. Add the following:
|
(i) |
kg g 37 87 + 11 11 _____________ |
(ii) |
kg g 13 60 + 61 20 _____________ |
|
(iii) |
kg g 54 84 + 27 40 _____________ |
(iv) |
kg g 74 15 + 17 18 _____________ |
|
(v) |
kg g 96 35 + 42 53 _____________ |
(vi) |
kg g 12 83 + 14 17 _____________ |
|
(vii) |
kg g 18 56 + 07 37 _____________ |
(viii) |
kg g 54 45 + 37 48 _____________ |
|
(ix) |
kg g 56 904 38 417 + 112 568 ______________ |
(x) |
kg g 65 394 09 678 + 83 467 ______________ |
|
(xi) |
kg g 26 760 14 650 + 79 480 ______________ |
(xii) |
kg g 53 350 36 150 + 63 100 ______________ |
|
(xiii) |
kg g 76 706 19 890 + 17 700 ______________ |
(xiv) |
kg g 13 576 46 695 + 20 800 ______________ |
|
(xv) |
kg g 18 985 15 850 + 16 250 ______________ |
(xvi) |
kg g 25 705 25 350 + 63 111 ______________ |
Answer:
IV. (i) 48 kg 98 g
(ii) 74 kg 80 g
(iii) 81 kg 124 g
(iv) 91 kg 33 g
(v) 138 kg 88 g
(vi) 26 kg 100 g
(vii) 25 kg 93 g
(viii) 91 kg 93 g
(ix) 207 kg 889 g
(x) 158 kg 539 g
(xi) 120 kg 890 g
(xii) 152 kg 600 g
(xiii) 114 kg 296 g
(xiv) 81 kg 71 g
(xv) 51 kg 85 g
(xvi) 114 kg 166 g
● Related Concepts
● Conversion of Standard Unit of Mass
From Addition of Mass to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
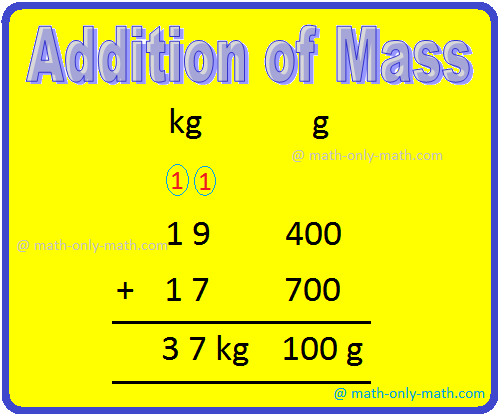



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.