Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Intersecting Lines
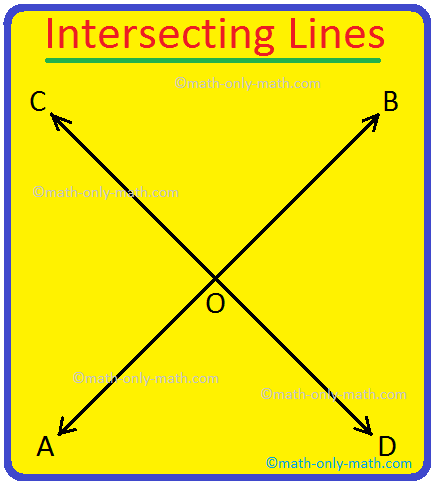
Two lines that cross each other at a particular point are called intersecting lines. The point where two lines cross is called the point of intersection.
Definition of Intersecting Lines:
If two lines have one common point, they are called intersecting lines.
For Example:
(i) Two adjacent edges of a notebook
(ii) Crossing roads
(iii) The multiplication sign (×) etc. are the examples of the intersecting lines.
In the given figure \(\underset{AB}{\leftrightarrow}\) and \(\underset{CD}{\leftrightarrow}\) intersect each other at point O.
Working Rules to Draw Intersecting Lines:
Step I: Draw a line \(\overleftrightarrow{AB}\) and another line \(\overleftrightarrow{CD}\).
Step II: Let them intersect each other at a point O.
Step III: The point of intersection O lies on line AB as well as on line CD.
Now, we can say that lines AB and CD are intersecting lines. They intersect at one point O.
From Intersecting Lines to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.