Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Integers
The notation of a number is connected with the act of counting. So, the natural numbers 1, 2, 3, 4, 5, …… are also called counting numbers. We use ten symbols or digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 to denote large numbers by using position of the digits in the given number.
So far, we have been dealing with natural numbers and whole numbers. While studying the properties of whole numbers, we found that the closure property does not hold good for the subtraction of natural numbers as well as whole numbers. This is because of the following:
25 - 20 = 5 is a whole number as well as a natural number.
25 - 25 = 0 is a whole number but not a natural number.
25 - 30 = - 5 which is neither a whole number nor a natural number
Hence, negative numbers are needed and are added in our number system.
The numbers discovered first were natural numbers i.e., 1, 2, 3, 4, 5, 6, ......
If 0 is included to the collection of natural numbers, we get a collection of whole numbers. i.e., 0, 1, 2, 3, 4, 5, 6, ......
There are negative numbers too, i.e., the system of whole numbers together with negative numbers are called integers i.e., -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ......
The system of integers consists of the following:
(i) natural numbers i.e. 1, 2, 3, 4, 5, 6,......
(ii) zero i.e., 0
(iii) whole numbers i.e., 0, 1, 2, 3, 4, 5, 6, ......
(iv) negative numbers i.e., -1, -2, -3, -4, -5, -6, ......
What are integers?
The negative numbers, zero and the natural numbers together are called integers.
A collection of numbers which is written as …….. -4, -3, -2, -1, 0, 1, 2, 3, 4……… .
These numbers are called integers.
Numbers that represent displacement considering direction are called directed numbers. They are also called signed numbers, because of the '+' or '-' sign which is a part of these numbers.
The collection of all whole numbers along with the negative numbers -1, -2, -3, -4, ... is called the collection (or set) of integers. It is denoted by I or Z.
Thus, Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
According to set theory
Integers, {...-6, -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, ...}
For example:
(i) -8, -2, 0, 2, 8
(ii) -7, -1, 0, 5, 12
(iii) -15, -9, 11, 21
(iv) -10, -3, 0, 9, 14
(v) -6, -4, 0, 7, 19
New numbers denoted by -1, -2, -3, -4, -5, -6, ...... called minus one, minus two, minus three, minus four...... respectively are introduced corresponding to numbers 1. 2, 3, 4, 5, 6, ...... such that
|
1 + (-1) = 0 2 + (-2) = 0 3 + (-3) = 0 4 + (-4) = 0 5 + (-5) = 0 6 + (-6) = 0 and so on. |
1 and -1 are opposite numbers. 2 and -2 are opposite numbers. 3 and -3 are opposite numbers. 4 and -4 are opposite numbers. 5 and -5 are opposite numbers. 6 and -6 are opposite numbers and so on. |
The combination of the new collection of timbers with whole timber 0, 1, 2, 3, 4, 5, 6, ...... are called integers.
Note: ✅ For every positive number, there exists a negative number.
✅ The sum of any positive number and its negative is equal to zero (0), that is, 1 + (-1) = 0, 24 + (-24) = 0, etc.
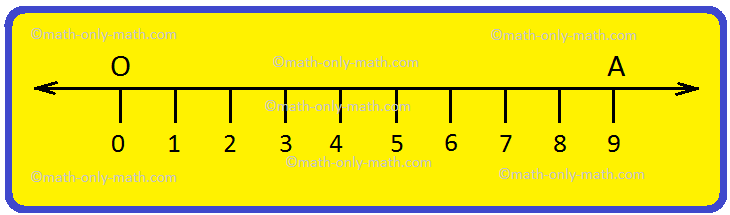
We usually represent numbers by making evenly spaced points one unit apart on a straight horizontal line which is called a number line. The line extends indefinitely to the left and to the right. A point O on the line, called the origin corresponds to the number 0. So, point A at a distance of 9 units to the right of zero represents the number 9 on the number line shown below.
|
What lies on the left of 0? Let us think about some of the familiar things to understand about the positive number and the negative number. We very often hear that the temperature during winter went down to -2°. We know that the temperature in -2° is very cold, it is colder than 0°c. It means that -2 is smaller than 0. Let us see in a thermometer where -2 is located. It is marked below 0. To
measure the depth below the ground level we use negative numbers. Here, 0
indicated ground level. On a number line a number that is right to the 0 is
positive and a number left side to the 0 is negative. So, we have a new set of
numbers -1, -2, -3, -4, -5, ….. These are known as the negative numbers. |
On the number line there are positive numbers, negative numbers and 0. These are called integers. 0 is neither positive nor negative.
The sign before the number indicates its direction to the right or left of 0. For example +5 indicates that the number lies to the right of 0 and -5 indicates that the number lies to the left of 0. Thus, integers are also called directed numbers. If a number has no sign it means that it is a positive integer.
Negative Integers:
The negative numbers ………. -5, -4, -3, -2, -1 are called negative integers.
Thus, examples of negative integers are ……… -5, -4, -3, -2, -1.
Note:
We use the symbol ‘-’ to denote negative integers and the same symbol is used to indicate subtraction. But the context will always make it clear whether we mean negative integer or subtraction.
Positive Integers:
The natural numbers 1, 2, 3, 4, 5, ……… are called positive integers.
Thus, examples of positive integers are 1, 2, 3, 4, 5, ………. .
Note:
Positive integers are also written as +1, +2, +3, +4, +5, ………… however, the plus sign (+) is usually omitted and understood.
The number 0 is simply an integer. It is neither positive nor negative.
i.e., 'Zero' is an integer which is neither positive not negative.
In real life, integers are used to represent opposite situations.
For example:
|
Positive Integers |
Negative Integers | |
|
(i) |
Profit |
Loss |
|
(ii) |
Deposits in banks |
Withdrawals from banks |
|
(iii) |
Temperatures above 0°C |
Temperatures below D°C |
|
(iv) |
Above sea level |
Below sea level |
Frequently Asked Questions and Answers on Integers:
1. Are all natural numbers integers?
1. Are all natural numbers integers?
Answer:
Yes, all natural numbers are integers.
The natural numbers are 1, 2, 3, 4, 5, 6, ……
The negative numbers, zero and the natural numbers together are called integers., such as -4, -3, -2, -1, 0, 1, 2, 3, and so on. Since all whole numbers are natural numbers, all natural numbers are also integers.
2. Are all whole numbers integers?
2. Are all whole numbers integers?
Answer:
Yes, all whole numbers are integers.
The negative numbers, zero and the natural numbers together are called integers., such as .... -4, -3, -2, -1, 0, 1, 2, 3, ... and so on. So, all whole numbers are integers.
3. Which integers are not whole numbers?
3. Which integers are not whole numbers?
Answer:
All negative integers are not whole numbers.
4. Write the smallest positive integer?
4. Write the smallest positive integer?
Answer:
The smallest positive integer is 1.
Note: 0 is the smallest whole number, but 0 is neither positive nor negative.
5. What are negative integers?
5. What are negative integers?
Answer:
The numbers -1, -2, -3, -4, -5, -6, ... are called the collection of negative integers.
6. What are positive integers?
6. What are positive integers?
Answer:
The numbers 1, 2, 3, 4, 5, 6, ... are called the collection of positive integers.
● Integers
Representation of Integers on a Number Line.
Addition of Integers on a Number Line.
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

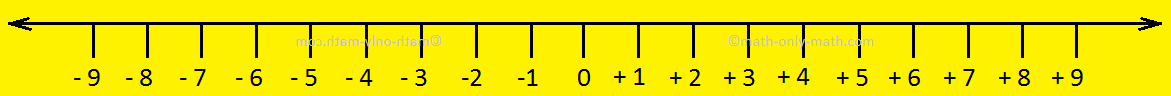


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.