Real Life Problems on Percentage
Real life problems on percentage will help us to solve different types of problems related to the real-life situations. To understand the procedures follow step-by-step explanation so that you can solve any other similar type of percentage problems.
Solved real life problems on percentage:
1. Mike needs 30% to pass. If he scored 212 marks and falls short by 13 marks, what was the maximum marks he could have got?
Solution:
If Mike had scored 13 marks more, he could have scored 30%
Therefore, Mike required 212 + 13 = 225 marks
Let the maximum marks be m.
Then 30 % of m = 225
(30/100) × m = 225
m = (225 × 100)/30
m = 22500/30
m = 750
2. A number is increased by 40 % and then decreased by 40 %. Find the net increase or decrease per cent.
Solution:
Let the number be 100.
Increase in the number = 40 % = 40 % of 100
= (40/100 × 100)
= 40
Therefore, increased number = 100 + 40 = 140
This number is decreased by 40 %
Therefore, decrease in number = 40 % of 140
= (40/100 × 140)
= 5600/100
= 56
Therefore, new number = 140 - 56 = 84
Thus, net decreases = 100 - 84 = 16
Hence, net percentage decrease = (16/100 × 100) %
= (1600/100) %
= 16 %
3. Max scored 6 marks more than what he did in the previous examination in which he scored 30. Maria scored 30 marks more than she did in the previous examination in which she scored 60. Who showed less improvement?
Solution:
Max percentage improvement in the first exam = (6/30 × 100) %
= (600/30) %
= 20 %
Maria percentage improvement in the first exam = (30/60 × 100) %
= (3000/60) %
= 50 %
Hence, 20 % < 50 %
Therefore, Max showed less improvement.
Percentage of the given Quantity
How much Percentage One Quantity is of Another?
Real Life Problems on Percentage
8th Grade Math Practice
From Real Life Problems on Percentage to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
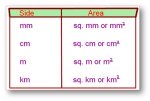
Area | Units to find Area | Conversion Table of Area | Two Dimensional
Apr 27, 24 01:53 PM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
Worksheet on Use of Decimal | Free Printable Decimals Worksheets
Apr 27, 24 01:45 PM
Practice the questions given in the worksheet on use of decimals in calculating money, in measuring the length, in measuring the distance, in measuring the mass and in measuring the capacity. -
Adding 1-Digit Number | Understand the Concept one Digit Number
Apr 26, 24 01:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
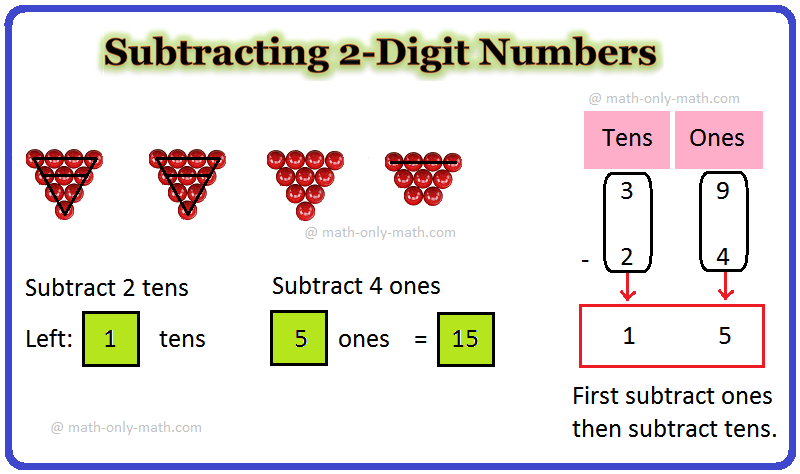
Subtracting 2-Digit Numbers | How to Subtract Two Digit Numbers?
Apr 26, 24 12:36 PM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
1st Grade Word Problems on Subtraction | Subtracting 2-Digit Numbers
Apr 26, 24 12:06 PM
In 1st grade word problems on subtraction students can practice the questions on word problems based on subtraction. This exercise sheet on subtraction can be practiced by the students to get more ide…
Worksheet on Fraction into Percentage
Worksheet on Percentage into Fraction
Worksheet on Percentage into Ratio
Worksheet on Ratio into Percentage
Worksheet on Percentage into Decimal
Worksheet on Percentage of a Number
Worksheet on Finding Value of a Percentage
Worksheet on Percentage of a Given Quantity
Worksheet on Word Problems on Percentage
Worksheet on Increase Percentage
Worksheet on Decrease Percentage
Worksheet on increase and Decrease Percentage

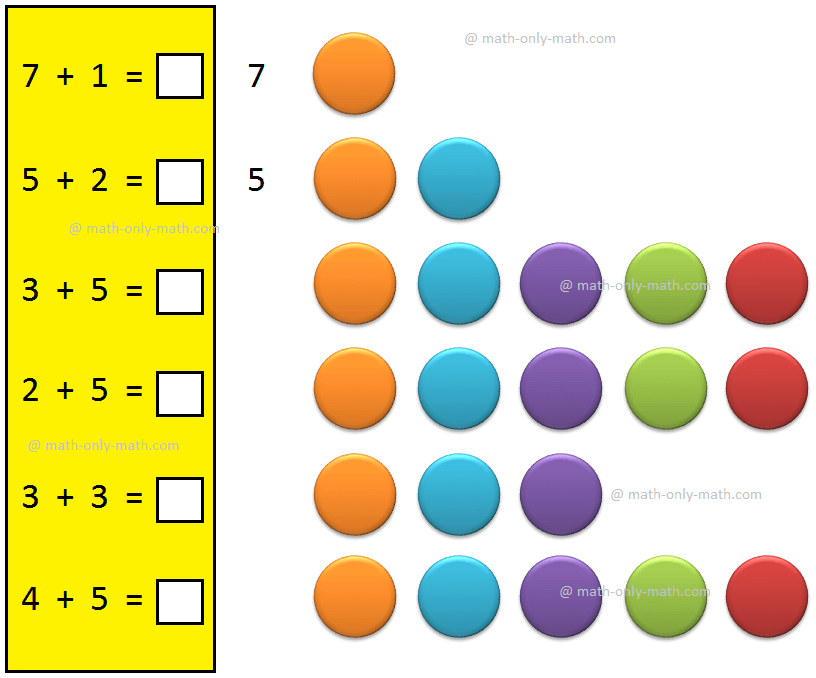

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.