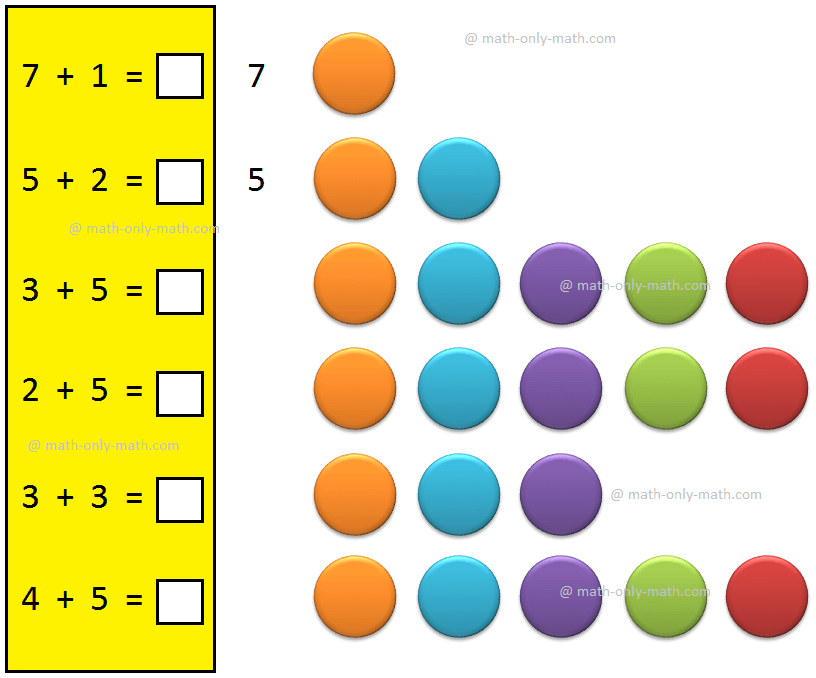Exact Value of cos 7½°
How to find the exact value of cos 7½° using the value of cos 15°?
Solution:
7½° lies in the first quadrant.
Therefore, cos 7½° is positive.
For all values of the angle A we know that, cos (α - β) = cos α cos β + sin α sin β.
Therefore, cos 15° = cos (45° - 30°)
cos 15° = cos 45° cos 30° + sin 45° sin 30°
= \(\frac{1}{√2}\)∙\(\frac{√3}{2}\) + \(\frac{1}{√2}\)∙\(\frac{1}{2}\)
= \(\frac{√3}{2√2}\) + \(\frac{1}{2√2}\)
= \(\frac{√3 + 1}{2√2}\)
Again for all values of the angle A we know that, cos A = 2 cos\(^{2}\)\(\frac{A}{2}\) - 1
⇒
1 + cos A = 2 cos\(^{2}\) \(\frac{A}{2}\)
⇒
2 cos\(^{2}\) \(\frac{A}{2}\) = 1 + cos A
⇒
2 cos\(^{2}\) 7½˚ = 1 + cos 15°
⇒
cos\(^{2}\) 7½˚ = \(\frac{1 + cos 15°}{2}\)
⇒ cos\(^{2}\) 7½˚ = \(\frac{1 + \frac{√3 + 1}{2√2}}{2}\)
⇒
cos\(^{2}\) 7½˚ = \(\frac{2√2 + √3 + 1}{4√2}\)
⇒
cos 7½˚ = \(\sqrt{\frac{4 + √6 + √2}{8}}\), [Since cos 7½° is positive]
⇒ cos 7½˚ = \(\frac{\sqrt{4 + √6 + √2}}{2√2}\)
Therefore, cos 7½˚ = \(\frac{\sqrt{4 + √6 + √2}}{2√2}\)
- Trigonometric Ratios of Angle A2A2
- Trigonometric Ratios of Angle A3A3
- Trigonometric Ratios of Angle A2A2 in Terms of cos A
- tan A2A2 in Terms of tan A
- Exact value of sin 7½°
- Exact value of cos 7½°
- Exact value of tan 7½°
- Exact Value of cot 7½°
- Exact Value of tan 11¼°
- Exact Value of sin 15°
- Exact Value of cos 15°
- Exact Value of tan 15°
- Exact Value of sin 18°
- Exact Value of cos 18°
- Exact Value of sin 22½°
- Exact Value of cos 22½°
- Exact Value of tan 22½°
- Exact Value of sin 27°
- Exact Value of cos 27°
- Exact Value of tan 27°
- Exact Value of sin 36°
- Exact Value of cos 36°
- Exact Value of sin 54°
- Exact Value of cos 54°
- Exact Value of tan 54°
- Exact Value of sin 72°
- Exact Value of cos 72°
- Exact Value of tan 72°
- Exact Value of tan 142½°
- Submultiple Angle Formulae
- Problems on Submultiple Angles
11 and 12 Grade Math
From Exact Value of cos 7 and Half Degree to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Adding 1-Digit Number | Understand the Concept one Digit Number
Apr 26, 24 01:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
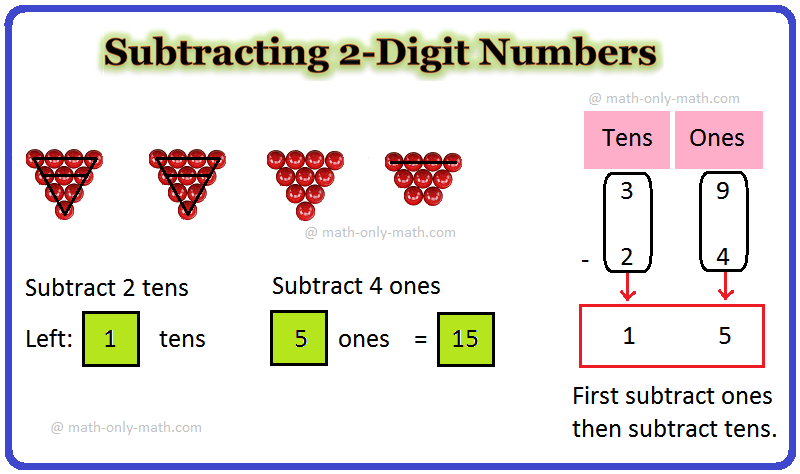
Subtracting 2-Digit Numbers | How to Subtract Two Digit Numbers?
Apr 26, 24 12:36 PM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
1st Grade Word Problems on Subtraction | Subtracting 2-Digit Numbers
Apr 26, 24 12:06 PM
In 1st grade word problems on subtraction students can practice the questions on word problems based on subtraction. This exercise sheet on subtraction can be practiced by the students to get more ide… -
Subtracting 1-Digit Number | Subtract or Minus Two One-Digit Number
Apr 26, 24 11:21 AM
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction me… -
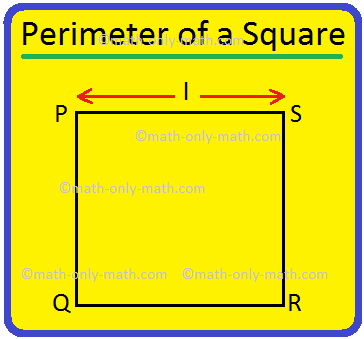
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete…