Exact Value of cos 27°
We will learn to find the exact value of cos 27 degrees using the formula of submultiple angles.
How to find the exact value of cos 27°?
Solution:
We have, (sin 27° + cos 27°)\(^{2}\) = sin\(^{2}\) 27° + cos\(^{2}\) 27° + 2 sin 27° cos 27°
⇒ (sin 27° + cos 27°)\(^{2}\) = 1 + sin 2 ∙ 27°
⇒ (sin 27° + cos 27°)\(^{2}\) = 1 + sin 54°
⇒ (sin 27° + cos 27°)\(^{2}\) = 1 + sin (90° - 36°)
⇒ (sin 27° + cos 27°)\(^{2}\) = 1 + cos 36°
⇒ (sin 27° + cos 27°)\(^{2}\) = 1+ \(\frac{√5 +1}{4}\)
⇒ (sin 27° + cos 27°)\(^{2}\) = \(\frac{1}{4}\) ( 5 + √ 5)
Therefore, sin 27° + cos 27° = \(\frac{1}{2}\sqrt{5 + \sqrt{5}}\) …………….….(i)
[Since, sin 27° > 0 and cos 27° > 0)
Similarly, we
have,
(sin 27° - cos 27°)\(^{2}\) = 1 - cos 36°
⇒ (sin 27° - cos 27°)\(^{2}\) = 1 - \(\frac{√5 + 1}{4}\)
⇒ (sin 27° - cos 27°)\(^{2}\) = \(\frac{1}{4}\) (3 - √5
)
Therefore, sin 27° - cos 27° = ± \(\frac{1}{2}\sqrt{3 - \sqrt{5}}\)
…………….….(ii)
Now, sin 27° - cos 27° = √2 (\(\frac{1}{√2}\)
sin 27˚ - \(\frac{1}{√2}\) cos 27°)
= √2 (cos 45° sin 27° - sin 45° cos 27°)
= √2 sin (27° - 45°)
= -√2 sin 18° < 0
Therefore, from (ii) we get,
sin 27° - cos 27° = -\(\frac{1}{2}\sqrt{3 - \sqrt{5}}\) …………….….(iii)
Now, subtracting (iii) and (i) we get,
2 cos 27° = \(\frac{1}{2}\sqrt{5 + \sqrt{5}}\) + \(\frac{1}{2}\sqrt{3 - \sqrt{5}}\)
⇒ cos 27° = \(\frac{1}{4}(\sqrt{5 + \sqrt{5}} + \sqrt{3 - \sqrt{5}})\)
Therefore, cos 27° = \(\frac{1}{4}(\sqrt{5 + \sqrt{5}} + \sqrt{3 - \sqrt{5}})\)
- Trigonometric Ratios of Angle \(\frac{A}{2}\)
- Trigonometric Ratios of Angle \(\frac{A}{3}\)
- Trigonometric Ratios of Angle \(\frac{A}{2}\) in Terms of cos A
- tan \(\frac{A}{2}\) in Terms of tan A
- Exact value of sin 7½°
- Exact value of cos 7½°
- Exact value of tan 7½°
- Exact Value of cot 7½°
- Exact Value of tan 11¼°
- Exact Value of sin 15°
- Exact Value of cos 15°
- Exact Value of tan 15°
- Exact Value of sin 18°
- Exact Value of cos 18°
- Exact Value of sin 22½°
- Exact Value of cos 22½°
- Exact Value of tan 22½°
- Exact Value of sin 27°
- Exact Value of cos 27°
- Exact Value of tan 27°
- Exact Value of sin 36°
- Exact Value of cos 36°
- Exact Value of sin 54°
- Exact Value of cos 54°
- Exact Value of tan 54°
- Exact Value of sin 72°
- Exact Value of cos 72°
- Exact Value of tan 72°
- Exact Value of tan 142½°
- Submultiple Angle Formulae
- Problems on Submultiple Angles
11 and 12 Grade Math
From Exact Value of cos 27° to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
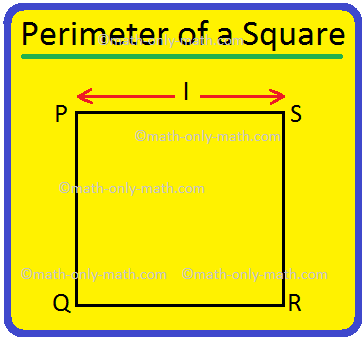
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
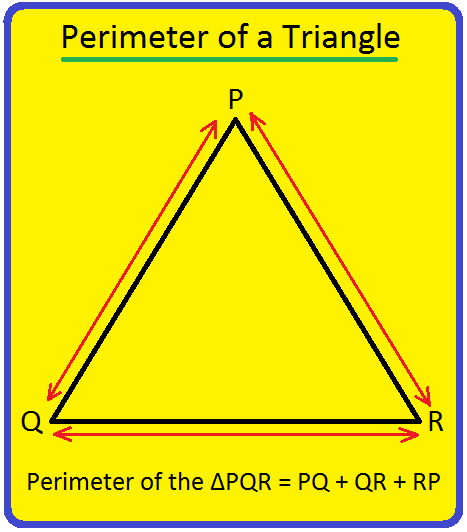
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
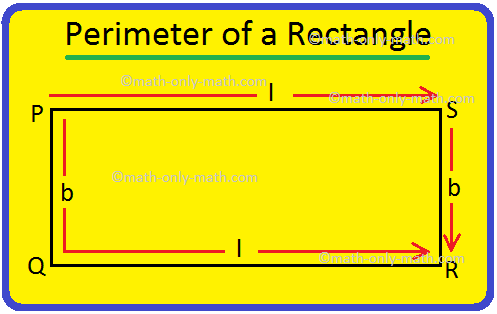
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…