Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Exact Value of cos 22½°
How to find the exact value of cos 22½° using the value of cos 45°?
Solution:
22½° lies in the first quadrant.
Therefore, sin 22½° is positive.
For all values of the angle A we know that, cos A = 2 cos2 A2 - 1
⇒ 1 + cos A = 2 cos2 A2
⇒ 2 cos2 A2 = 1 + cos A
⇒ 2 cos2 22½˚ = 1 + cos 45°
⇒ cos2 22½˚ = 1+cos45°2
⇒ sin2 22½˚ = 1+1√22, [Since we know cos 45° = 1√2]
⇒ cos 22½˚ = √12(1+1√2), [Since, cos 22½˚ > 0]
⇒ cos 22½˚ = √√2+12√2
⇒ cos 22½˚ = 12√2+√2
Therefore, cos 22½˚ = 12√2+√2
- Trigonometric Ratios of Angle A2A2
- Trigonometric Ratios of Angle A3A3
- Trigonometric Ratios of Angle A2A2 in Terms of cos A
- tan A2A2 in Terms of tan A
- Exact value of sin 7½°
- Exact value of cos 7½°
- Exact value of tan 7½°
- Exact Value of cot 7½°
- Exact Value of tan 11¼°
- Exact Value of sin 15°
- Exact Value of cos 15°
- Exact Value of tan 15°
- Exact Value of sin 18°
- Exact Value of cos 18°
- Exact Value of sin 22½°
- Exact Value of cos 22½°
- Exact Value of tan 22½°
- Exact Value of sin 27°
- Exact Value of cos 27°
- Exact Value of tan 27°
- Exact Value of sin 36°
- Exact Value of cos 36°
- Exact Value of sin 54°
- Exact Value of cos 54°
- Exact Value of tan 54°
- Exact Value of sin 72°
- Exact Value of cos 72°
- Exact Value of tan 72°
- Exact Value of tan 142½°
- Submultiple Angle Formulae
- Problems on Submultiple Angles
11 and 12 Grade Math
From Exact Value of cos 22 and Half Degree to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
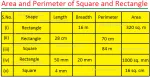
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
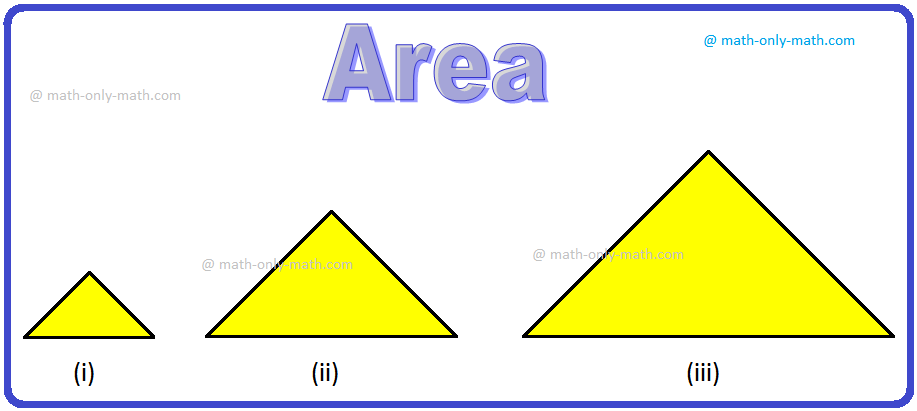
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
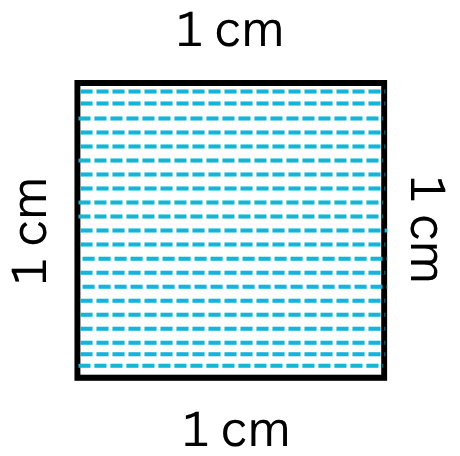
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
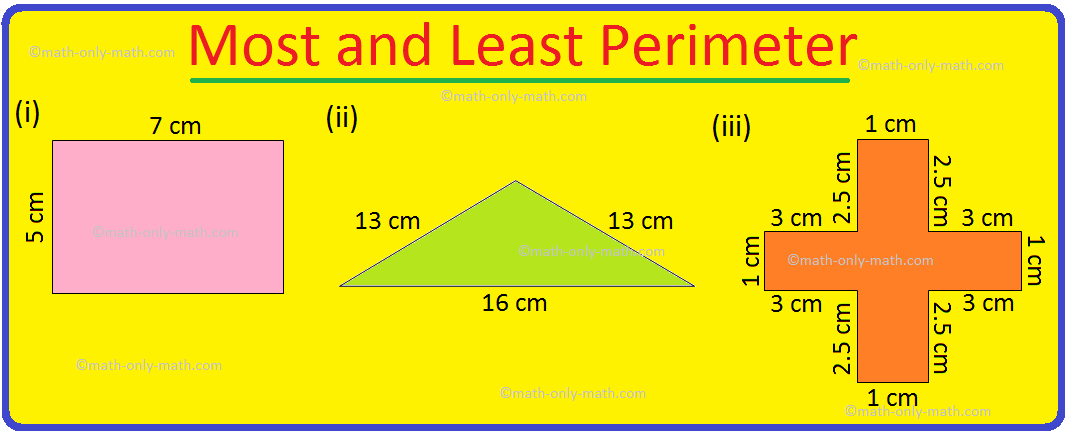
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.