Centre of the Circle on x-axis
We will learn how to find the equation when the centre of a circle on x-axis.
The equation of a circle with centre at (h, k) and radius equal to a, is (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\).
When the centre of a circle is on the x-axis i.e., k = 0.
Then the equation (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\) becomes (x - h)\(^{2}\) + y\(^{2}\) = a\(^{2}\) ⇒ x\(^{2}\) + y\(^{2}\) - 2hx + h\(^{2}\) = a\(^{2}\) ⇒ x\(^{2}\) + y\(^{2}\) - 2hx + h\(^{2}\) – a\(^{2}\) = 0
If the centre of a circle be on the x-axis, then the y co-ordinate of the centre will be zero. Hence, the general form of the equation of the circle will be of the form x\(^{2}\) + y\(^{2}\) + 2gx + c = 0, where g and c are the constants.
Solved examples on
the central form of the equation of a circle whose centre is on the
x-axis:
1. Find the equation of a circle whose centre of a circle is on the x-axis at -5 and radius is 9 units.
Solution:
Radius of the circle = 9 units.
Since, centre of a circle be on the x-axis, then the y co-ordinate of the centre will be zero.
The required equation of the circle whose centre of a circle is on the x-axis at -5 and radius is 9 units is
(x + 5)\(^{2}\) + y\(^{2}\) = 9\(^{2}\)
⇒ x\(^{2}\) + 10x + 25 + y\(^{2}\) = 81
⇒ x\(^{2}\) + y\(^{2}\) + 10x + 25 - 81 = 0
⇒ x\(^{2}\) + y\(^{2}\) + 10x - 56 = 0
2. Find the equation of a circle whose centre of a circle is on the x-axis at 2 and radius is 3 units.
Solution:
Radius of the circle = 3 units.
Since, centre of a circle be on the x-axis, then the y co-ordinate of the centre will be zero.
The required equation of the circle whose centre of a circle is on the x-axis at 2 and radius is 3 units is
(x - 2)\(^{2}\) + y\(^{2}\) = 3\(^{2}\)
⇒ x\(^{2}\) - 4x + 4 + y\(^{2}\) = 9
⇒ x\(^{2}\) + y\(^{2}\) - 4x + 4 - 9 = 0
⇒ x\(^{2}\) + y\(^{2}\) - 4x - 5 = 0
● The Circle
- Definition of Circle
- Equation of a Circle
- General Form of the Equation of a Circle
- General Equation of Second Degree Represents a Circle
- Centre of the Circle Coincides with the Origin
- Circle Passes through the Origin
- Circle Touches x-axis
- Circle Touches y-axis
- Circle Touches both x-axis and y-axis
- Centre of the Circle on x-axis
- Centre of the Circle on y-axis
- Circle Passes through the Origin and Centre Lies on x-axis
- Circle Passes through the Origin and Centre Lies on y-axis
- Equation of a Circle when Line Segment Joining Two Given Points is a Diameter
- Equations of Concentric Circles
- Circle Passing Through Three Given Points
- Circle Through the Intersection of Two Circles
- Equation of the Common Chord of Two Circles
- Position of a Point with Respect to a Circle
- Intercepts on the Axes made by a Circle
- Circle Formulae
- Problems on Circle
11 and 12 Grade Math
From Centre of the Circle on x-axis to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
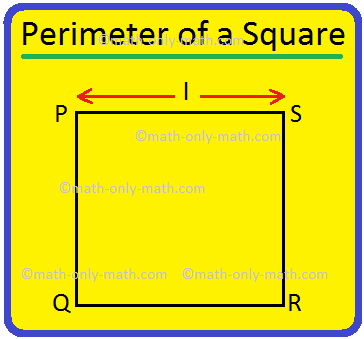
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
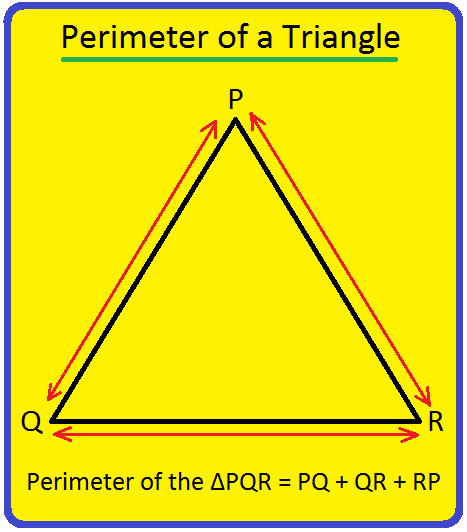
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
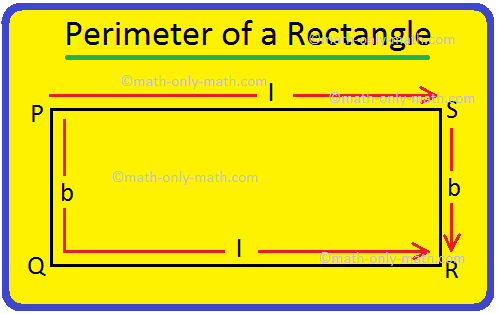
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…