Worksheet on Decimal Numbers

Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts.

The questions on decimal worksheets below include the decimal number system such as converting fractions to decimals; converting decimals to fractions in its lowest terms; writing the decimal places and their place values; converting the unlike decimals to like decimals; etc., will help your child to get valuable practice to improve in math.

⦿ The fractions with the denominators 10, 100, 1000, etc, are known as decimai fractions or simply decimals.

⦿ A decimal consists of two parts- the whole number part and the decimal part.

⦿ While reading a decimal number, its decimal part is read digit-wise.

⦿ The number of digits contained in the decimal part of a decimal gives the number of its decimal place.

⦿ Decimals having the same number of decimal places are called like decimals.

⦿ Decimals having different number of decimal places are called unlike decimals.

⦿ We can convert decimals into fractions and vice-versa.

1. State True or False

(i) 0.31 and 17.002 are like decimals.

(ii) 2.126 and 2.018 are unlike decimals.

(iii) 107.465 and 0.009 are like decimals.

(iv) 8.6 is smaller than 10.6.

(v) 34.57 is greater than 16.357.

(vi) 81.06 is smaller than 80.9.

(vii) 1 + $\frac{3}{10}$ + $\frac{2}{1000}$ = 1.302

(viii) $\frac{341}{1000}$ = 0.342

(ix) 3 kg 8 g is equal to 3.800 kg.

(x) The value of $\frac{6}{25}$ is 0.024.

(xi) 1024 ml = 10.24 litre.

2. Write each of the following as decimals:

(a) $\frac{5}{100}$

(b) $\frac{17}{10}$

(c) $\frac{87}{1000}$

(d) $\frac{9}{100}$

(e) $\frac{81}{1000}$

(f) $\frac{2222}{100}$

3. Express each of the following as decimals and find the number of decimal places in each.

(a) $\frac{37}{100}$

(b) $\frac{11}{1000}$

(c) $\frac{9}{100}$

(d) $\frac{739}{10}$

(e) $\frac{1234}{1000}$

(f) $\frac{495}{10}$

4. Express each of the following as decimals:

(a) $\frac{17}{5}$

(b) $\frac{231}{2}$

(c) $\frac{1297}{4}$

(d) $\frac{347}{50}$

(e) $\frac{1234}{25}$

5. Express each of the following as fractions:

(a) 3.47

(b) 17.001

(c) 0.97

(d) 2.09

(e) 0.009

6. Express each of the following as fractions in the lowest form:

(a) 18.64

(b) 0.008

(c) 165.2

(d) 0.28

(e) 3.5

7. Write the place and place value of the underlined digits:

(a) 8.013

(b) 53.31

(c) 100.92

(d) 11.381

(e) 0.004

8. Convert each of these unlike decimals into like decimals:

(a) 0.1, 3.68, 1

(b) 1.11, 12.754, 92.5, 17

(c) 8.39, 9.236, 24.8, 263.07, 3

(d) 0.91, 65.87, 21, 9.3064

(e) 8.5, 2.04, 3.0075

(f) 24.6, 2.83, 0.951

(g) 1.14, 2.8, 7.003, 0.0124

(h) 0.13, 23.5, 1.9

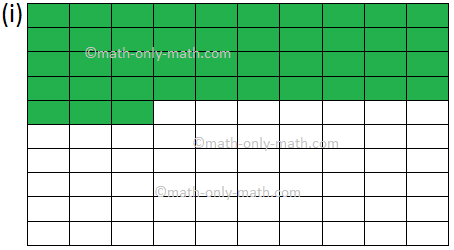
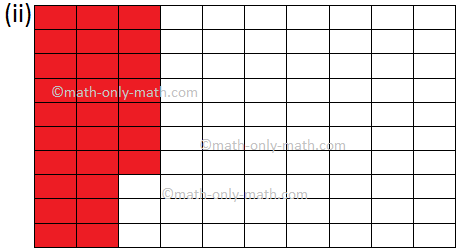
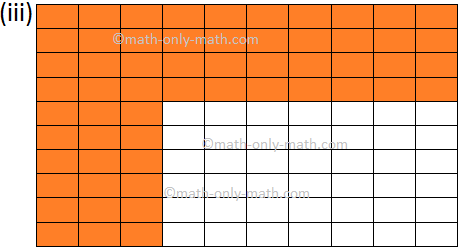
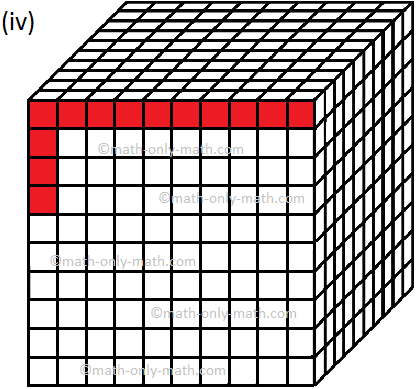
9. Write the fractional number and decimal number for the shaded part of each figure.

10. Represent the following decimal numbers on the number line.

(i) 0.1

(ii) 0.3

(iii) 1.5

(iv) 2.9

11. Between which two whole numbers on the number line does the given number lie?

(i) 0.8

(ii) 3.6

(iii) 12.23

(iv) 0.39

12. Write the following decimals in words.

(i) 4.5

(ii) 88.9

(iii) 34.05

(iv) 265.72

(v) 6.715

(vi) 18.025

(vi) 83.031

(viii) 408.007

13. Write each of the following as decimals.

(i) Eight tenths

(ii) Thirteen and four tenths

(iii) Seven hundred four point two

(iv) Ten point four six

(v) Sixty and three hundred nine thousandths

(vi) Four hundred two point two zero five

14. Write in decimal form:

(i) Twelve-hundredths

(ii) Twenty-three point zero five

(iii) Nine point zero zero one.

(iv) One hundred sixty-seven point three zero seven

15. Write each of the following decimals.

(i) $\frac{6}{100}$

(ii) $\frac{73}{10}$

(iii) $\frac{915}{1000}$

(iv) $\frac{615}{1000}$

(v) 17$\frac{1}{4}$

(vi) 8$\frac{1}{20}$

16. Multiple Choice Questions on (MCQ) Decimals:

   Tick (✔) the correct option.

(i) Two hundredths is written as:

(a) 2.00

(b) 0.200

(c) 0.02

(d) 200.0

(ii) $\frac{15}{25}$ can be expressed as:

(a) 0.15

(b) 0.25

(c) 15.25

(d) 0.6

(iii) 9.1 lies between the whole numbers:

(a) 0 and 1

(b) 9 and 1

(c) 9 and 10

(d) none of these

(iv) 800 + 30 + $\frac{1}{100}$ can be expressed as:

(i) 82.1

(ii) 830.01

(iii) 830.1

(iv) 803.01

(v)  Which is larger: 4.5 or 4.468?

(a) 4.468

(b) 4.5

(c) 830.1

(d) 803.01

(vi)  The sum of 3.8 and 8.3 is 

(a) 3.8

(b) 12.1

(c) 11.11

(d) 4.9

(vii) Jennifer purchased 5 kg 75 g of vegetables and 3 kg 465 g of fruits. The total weight of vegetables and fruits was:

(a) 8.450 kg

(b) 8.540 kg

(c) 8.054 kg

(d) 9.320 kg

17. Write the expanded form of

(i) 31.008

(ii) 19.857

(iii) 12.257

(iv) 18.703

18. Are 18.1 and 18.10 like decimals?

19. Arrange the following decimals in descending order:

          3.35, 2.59, 28.1, 6.0, 6.7, 3.5

20. Simplify:

(i) 7 - 0.3 + 2.5 - 0.03

(ii) 12.5 - 2.3 + 5 + 3 - 4.3

(iii) 13.5 - 3.3 + 2.5 - 5

21. Arrange the following decimals in ascending order:

         3.1001, 3.1, 3.01, 3.11, 3.001, 3.0101, 3.12

22. Fill in the blanks:

(i) Every decimal number can be represented on __________.

(ii) Decimals having different number of decimal places are called __________.

(iii) Eight hundredths = __________ = __________.

(iv) 0.53 lies between __________ and __________.

(v) __________ means fifteen hundredths.

(vi) 800 + 17 + 5 + 0.3 = __________.

23. Write the numerals for the following decimal number names.

(i) Eight point three eight

(ii) Fifteen point five zero seven

(iii) Sixty-five point four six nine

(iv) Four hundred and thirty-two point zero zero seven

(v) Three and six tenths

(vi) Fifty and eight hundredths

(vii) Six hundred and six thousandths

(viii) Five hundredths

(ix) Two thousand point one zero one

(x) Three hundred and three tenths and six hundredths

(xi) Two and five hundredths and two thousandths

(xii) Eight hundred and fifty one and six tenths

24. Write the number names for the following decimals.

(i) 2.437

(ii) 14.079

(iii) 96.627

(iv) 114.375

(v) 4.038

(vi) 0.038

(vii) 24.009

(viii) 246.439

(ix) 84.003

(x) 224.304

(xi) 501.617

(xii) 308.004

(xiii) 255.071

(xiv) 754.03

(xv) 218.499

25. Simplify the following addition and subtraction of decimals together:

(i) 140.005 + 69.38 - 94.385

(ii) 420 - 229.213 + 17.7

(iii) 91.345 - 85.428 + 60.438

(iv) 245.07 + 291.37 - 399.7

(v) 391.48 - 169.82 + 485.467

(vi) 747.155 - 649.38 + 485.467

(vii) 200.11 + 3.8 - 202.01

(viii) 993.185 - 486.925 + 24.3

(ix) 403.33 + 21.129 - 0.7

(x) 226.44 - 98.3 - 24.4

Answers for the worksheet on decimal numbers are given below to check the exact answers of the above decimal questions.

Answers:

1. (i) False

(ii) False

(iii) True

(iv) True

(v) True

(vi) False

(vii) True

(viii) False

(ix) False

(x) False

(xi) False

2. (a) 0.05

(b) 1.7

(c) 0.087

(d) 0.09

(e) 0.081

(f) 22.22

3. (a) 0.37; 2

(b) 0.011; 3

(c) 0.09; 2

(d) 73.9; 1

(e) 1.234; 3

(f) 49.5; 1

4. (a) 3.4

(b) 115.5

(c) 324.25

(d) 6.94

(e) 49.36

5. (a) $\frac{347}{100}$

(b) $\frac{17001}{1000}$

(c) $\frac{97}{100}$

(d) $\frac{209}{100}$

(e) $\frac{9}{1000}$

6. (a) $\frac{466}{25}$

(b) $\frac{1}{125}$

(c) $\frac{826}{5}$

(d) $\frac{7}{25}$

(e) $\frac{7}{2}$

7. (a) thousandths; 0.003

(b) tens; 50

(c) tenths; 0.9

(d) hundredths, 0.08

(e) tenths; 0

8. (a) 0.10, 3.68, 1.00

(b) 1.110, 12.754, 92.500, 17.000

(c) 8.390, 9.236, 24.800, 263.070, 3.000

(d) 0.9100, 65.8700, 21.0000, 9.3064

(e) 8.5000, 2.0400, 3.0075

(f) 24.600, 2.830, 0.951

(g) 1.1400, 2.8000, 7.0030, 0.0124

(h) 0.13, 23.50, 1.90

9. (i) Fractional Number: $\frac{43}{100}$ and Decimal Number: 0.43

(ii) Fractional Number: $\frac{27}{100}$ and Decimal Number: 0.27

(iii) Fractional Number: $\frac{58}{100}$ and Decimal Number: 0.58

(iv) Fractional Number: $\frac{13}{1000}$ and Decimal Number: 0.013

10.

11. (i) 0 to 1

(ii) 3 to 4

(iii) 12 to 13

(iv) 0 to 1

12. (i) Four point five

(ii) Eighty eight point nine

(iii) Thirty four point zero five

(iv) Two hundred sixty five point seven two

(v) Six point seven one five

(vi) Eighteen point zero two five

(vi) Eighty three point zero three one

(viii) Four hundred eight point zero zero seven

13. (i) 0.8

(ii) 13.4

(iii) 704.2

(iv) 10.46

(v) 60.309

(vi) 402.205

14. (i) 0.12

(ii) 23.05 

(iii) 9.009

(iv) 167.307

15. (i) 0.06

(ii) 7.3

(iii) 0.915

(iv) 0.615

(v) 17.25

(vi) 8.05

16. (i) Two hundredths is written as: (c) 0.02

(ii) $\frac{15}{25}$ can be expressed as: (d) 0.6

(iii) 9.1 lies between the whole numbers: (c) 9 and 10

(iv) 800 + 30 + $\frac{1}{100}$ can be expressed as (ii) 830.01

(v)  Which is larger: 4.5 or 4.468? (b) 4.5

(vi)  The sum of 3.8 and 8.3 is (b) 12.1

(vii) Jennifer purchased 5 kg 75 g of vegetables and 3 kg 465 g of fruits. The total weight of vegetables and fruits was: (b) 8.540 kg

17. (i) 30 + 1 + $\frac{8}{1000}$

(ii) 10 + 9 + $\frac{8}{10}$ + $\frac{5}{100}$ + $\frac{7}{1000}$

(iii) 10 + 2 +  $\frac{2}{10}$ + $\frac{5}{100}$ + $\frac{7}{1000}$

(iv) 10 + 8 + $\frac{7}{10}$ + $\frac{3}{1000}$

18. No, unlike decimals

19. 28.1, 6.7, 6.0, 3.5, 3.35, 2.59

20. (i) 9.17

(ii) 13.9

(iii) 7.7

21. 3.001, 3.01, 3.0101, 3.1, 3.1001, 3.11, 3.12

22. (i) Every decimal number can be represented on number line.

(ii) Decimals having different number of decimal places are called unlike decimals.

(iii) Eight hundredths = $\frac{8}{100}$ = 0.08.

(iv) 0.53 lies between 0 and 1.

(v) 0.15 means fifteen hundredths.

(vi) 800 + 17 + 5 + 0.3 = 822.3

Worksheet on Decimal Numbers

23. (i) 8.38

(ii) 15.507

(iii) 65.469

(iv) 432.007

(v) 3.6

(vi) 50.08

(vii) 600.006

(viii) 0.05

(ix) 2000.101

(x) 300.36

(xi) 2.052

(xii) 851.6

24. (i) Two point four three seven

(ii) Fourteen point zero seven nine

(iii) Ninety six point six two seven

(iv) One hundred fourteen point three seven five

(v) Four point zero three eight

(vi) Zero point zero three eight

(vii) Twenty four point zero zero nine

(viii) Two hundred forty six point four three nine

(ix) Eighty four point zero zero three

(x) Two hundred twenty four point three zero four

(xi) Five hundred one point six one seven

(xii) Three hundred eight point zero zero four

(xiii) Two hundred fifty five point zero seven one

(xiv) Seven hundred fifty four point zero three

(xv)  Two hundred eighteen point four nine nine

25. (i) 115

(ii) 208.487

(iii) 66.355

(iv) 136.74

(v) 707.127

(vi) 583.242

(vii) 1.9

(viii) 530.56

(ix) 423.759

(x) 103.74

Math Home work Sheets

7th Grade Math Problems

From Worksheet on Decimal Numbers to HOME PAGE