Problems on Trigonometric Ratios

Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation.

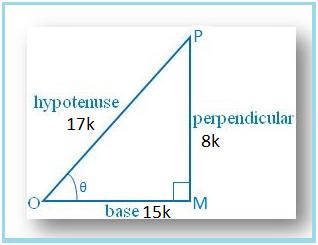
1. If sin θ = 8/17, find other trigonometric ratios of <θ.

Solution:

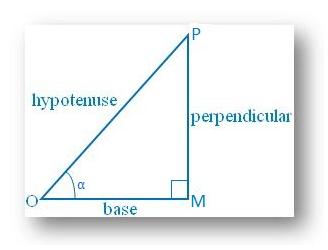
Let us draw a ∆ OMP in which ∠M = 90°.

Then sin θ = MP/OP = 8/17.

Let MP = 8k and OP = 17k, where k is positive.

By Pythagoras’ theorem, we get

OP² = OM² + MP²

⇒ OM² = OP² – MP²

⇒ OM² = [(17k)² – (8k)²]

⇒ OM² = [289k² – 64k²]

⇒ OM² = 225k²

⇒ OM = √(225k²)

⇒ OM = 15k

Therefore, sin θ = MP/OP = 8k/17k = 8/17

cos θ = OM/OP = 15k/17k = 15/17

tan θ = Sin θ/Cos θ = (8/17 × 17/15) = 8/15

csc θ = 1/sin θ = 17/8

sec θ = 1/cos θ = 17/15 and

cot θ = 1/tan θ = 15/8.

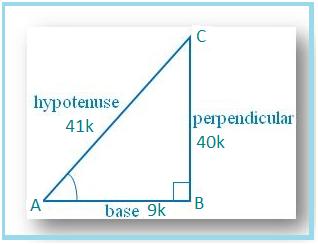
2. If Cos A = 9/41, find other trigonometric ratios of ∠A.

Solution:

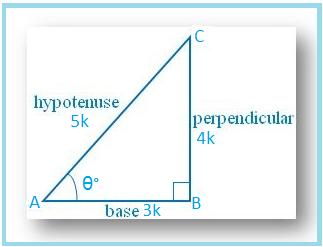
Let us draw a ∆ ABC in which ∠B = 90°.

Then cos θ = AB/AC = 9/41.

Let AB = 9k and AC = 41k, where k is positive.

By Pythagoras’ theorem, we get

AC² = AB² + BC²

⇒ BC² = AC² – AB²

⇒ BC² = [(41k)² – (9k)²]

⇒ BC² = [1681k² – 81k²]

⇒ BC² = 1600k²

⇒ BC = √(1600k²)

⇒ BC = 40k

Therefore, sin A = BC/AC = 40k/41k = 40/41

cos A = AB/AC = = 9k/41k = 9/41

tan A = Sin A/Cos A = (40/41 × 41/9) = 40/9

csc A = 1/sin A = 41/40

sec A = 1/cos A = 41/9 and

cot A = 1/tan A = 9/40.

3. Show that the value of sin θ and cos θ cannot be more than 1.

Solution:

We know, in a right angle triangle the hypotenuse is the longest side.

sin θ = perpendicular/hypotenuse = MP/OP < 1 since perpendicular cannot be greater than hypotenuse; sin θ cannot be more than 1.

Similarly, cos θ = base/hypotenuse = OM/OP < 1 since base cannot be greater than hypotenuse; cos θ cannot be more than 1.

4. Is that possible when A and B be acute angles, sin A = 0.3 and cos B = 0.7?

Solution:

Since A and B are acute angles, 0 ≤ sin A ≤ 1 and 0 ≤ cos B ≤ 1, that means the value of sin A and cos B lies between 0 to 1. So, it is possible that sin A = 0.3 and cos B = 0.7

5. If 0° ≤ A ≤ 90° can sin A = 0.4 and cos A = 0.5 be possible?

Solution:

We know that sin²A + cos²A = 1

Now put the value of sin A and cos A in the above equation we get;

(0.4)² + (0.5)² = 0.41 which is ≠ 1, sin A = 0.4 and cos A = 0.5 cannot be possible.



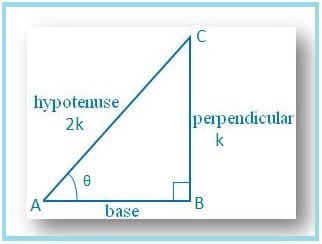
6. If sin θ = 1/2, show that (3cos θ - 4 cos³ θ) =0.

Solution:

Let us draw a ∆ ABC in which ∠B = 90° and ∠BAC = θ.

Then sin θ = BC/AC = 1/2.

Let BC = k and AC = 2k, where k is positive.

By Pythagoras’ theorem, we get

AC² = AB² + BC²

⇒ AB² = AC² – BC²

⇒ AB² = [(2k)² – k²]

⇒ AB² = [4k² – k²]

⇒ AB² = 3k²

⇒ AB = √(3k²)

⇒ AB = √3k.

Therefore, cos θ = AB/AC = √3k/2k = √3/2

Now, (3cos θ - 4 cos³ θ)

= 3√3/2 - 4 ×(√3/2)³

= 3√3/2 - 4 × 3√3/8

= 3√3/2 - 3√3/2

= 0

Hence, (3cos θ - 4 cos³ θ) = 0.

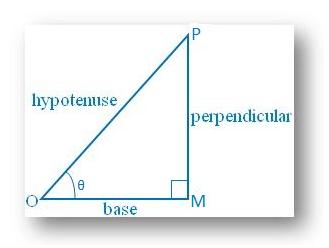
7. Show that sin α + cos α > 1 when 0° ≤ α ≤ 90°

Solution:

From the right triangle MOP,

Sin α = perpendicular/ hypotenuse

Cos α = base/ hypotenuse

Now, Sin α + Cos α

= perpendicular/ hypotenuse + base/ hypotenuse

= (perpendicular + base)/hypotenuse, which is > 1, Since we know that the sum of two sides of a triangle is always greater than the third side.

8. If cos θ = 3/5, find the value of (5csc θ - 4 tan θ)/(sec θ + cot θ)

Solution:

Let us draw a ∆ ABC in which ∠B = 90°.

Let ∠A = θ°

Then cos θ = AB/AC = 3/5.

Let AB = 3k and AC = 5k, where k is positive.

By Pythagoras’ theorem, we get

AC² = AB² + BC²

⇒ BC² = AC² – AB²

⇒ BC² = [(5k)² – (3k)²]

⇒ BC² = [25k² – 9k²]

⇒ BC² = 16k²

⇒ BC = √(16k²)

⇒ BC = 4k

Therefore, sec θ = 1/cos θ = 5/3

tan θ = BC/AB =4k/3k = 4/3

cot θ = 1/tan θ = 3/4 and

csc θ = AC/BC = 5k/4k = 5/4

Now (5csc θ -4 tan θ)/(sec θ + cot θ)

= (5 × 5/4 - 4 × 4/3)/(5/3 + 3/4)

= (25/4 -16/3)/(5/3 +3/4)

= 11/12 × 12/29

= 11/29

9. Express 1 + 2 sin A cos A as a perfect square.

Solution:

1 + 2 sin A cos A

= sin² A + cos² A + 2sin A cos A, [Since we know that sin² θ + cos² θ = 1]

= (sin A + cos A)²

10. If sin A + cos A = 7/5 and sin A cos A =12/25, find the values of sin A and cos A.

Solution:

sin A + cos A = 7/5

⇒ cos A = 7/5 - sin θ

Now from sin θ/cos θ = 12/25

We get, sin θ(7/5 - sin θ) = 12/25

or, 7 sin θ – 5 sin² θ = 12/5

or, 35 sin θ - 35 sin² θ = 12

or, 25sin² θ -35 sin θ + 12 = 0

or, 25 sin² θ -20 sin θ - 15 sin θ + 12 = 0

or, 5 sin θ(5 sin θ - 4) - 3(5 sin θ - 4) = 0

or, (5 sin θ - 3) (5 sin θ - 4) = 0

⇒ (5 sin θ - 3) = 0 or, (5 sin θ - 4) = 0

⇒ sin θ = 3/5 or, sin θ = 4/5

When sin θ = 3/5, cos θ = 12/25 × 5/3 = 4/5

Again, when sin θ = 4/5, cos θ = 12/25 × 5/4 = 3/5

Therefore, sin θ =3/5, cos θ = 4/5

or, sin θ =4/5, cos θ = 3/5.

11. If 3 tan θ = 4, evaluate (3sin θ + 2 cos θ)/(3sin θ - 2cos θ).

Solution: Given,

3 tan θ = 4

⇒ tan θ = 4/3

Now,

(3sin θ + 2 cos θ)/(3sin θ - 2cos θ)

= (3 tan θ + 2)/(3 tan θ - 2), [dividing both numerator and denominator by cos θ]

= (3 × 4/3 + 2)/(3 × 4/3 -2), putting the value of tan θ = 4/3

= 6/2

= 3.

12. If (sec θ + tan θ)/(sec θ - tan θ) = 209/79, find the value of θ.

Solution: (sec θ + tan θ)/(sec θ - tan θ) = 209/79

⇒ [(sec θ + tan θ) - (sec θ - tan θ)]/[(sec θ + tan θ) + (sec θ - tan θ)] = [209 – 79]/[209 + 79], (Applying componendo and dividendo)

⇒ 2 tan θ/2 sec θ =130/288

⇒ sin θ/cos θ × cos θ = 65/144

⇒ sin θ = 65/144.

13. If 5 cot θ = 3, find the value of (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ).

Solution:

Given 5 cot θ = 3

⇒ cot θ = 3/5

Now (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ)

= (5 - 3 cot θ)/(4 sin θ + 3 cot θ), [dividing both numerator and denominator by sin θ]

= (5 - 3 × 3/5)/(4 + 3 × 3/5)

= (5 - 9/5)/(4 + 9/5)

= (16/5 × 5/29)

= 16/29.

13. Find the value of θ (0° ≤ θ ≤ 90°), when sin² θ - 3 sin θ + 2 = 0

Solution:

⇒ sin² θ -3 sin θ + 2 = 0

⇒ sin² θ – 2 sin θ – sin θ + 2 = 0

⇒ sin θ(sin θ - 2) - 1(sin θ - 2) = 0

⇒ (sin θ - 2)(sin θ - 1) = 0

⇒ (sin θ - 2) = 0 or, (sin θ - 1) = 0

⇒ sin θ = 2 or, sin θ = 1

So, value of sin θ can’t be greater than 1,

Therefore sin θ = 1

⇒ θ = 90°

Basic Trigonometric Ratios 

Relations Between the Trigonometric Ratios

Problems on Trigonometric Ratios

Reciprocal Relations of Trigonometric Ratios

Trigonometrical Identity

Problems on Trigonometric Identities

Elimination of Trigonometric Ratios 

Eliminate Theta between the equations

Problems on Eliminate Theta 

Trig Ratio Problems

Proving Trigonometric Ratios

Trig Ratios Proving Problems

Verify Trigonometric Identities 

10th Grade Math

From Problems on Trigonometric Ratios to HOME PAGE