Area of Parallelogram
Here we will discuss about how to find the area of a parallelogram. To calculate area of parallelogram we need to remember the formula and solve step-by-step.
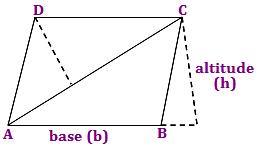
ABCD is a parallelogram with base (b) and altitude (h).
Area of parallelogram = 2 × Area of ∆ABC
= 2 × 1/2 × base × height sq. units
= 2 × 1/2 × AB × CE sq. units
= b × h sq. units
= base × height sq. units
Perimeter of parallelogram = 2(AB + BC)
= 2 × (Sum of adjacent sides)
Worked-out examples on area of parallelograms:
1. The base of the parallelogram is thrice its height. If the area is 192 cm², find the base and height.
Solution:
Let the height of the parallelogram = x cm
then the base of the parallelogram = 3x cm
Area of the parallelogram = 192 cm²
Area of parallelogram = base × height
192 = 3x × x
⇒ 3x² = 192
⇒ x² = 64
⇒ x = 8
Therefore, 3x = 3 × 8 = 24
Therefore, Base of the parallelogram is 24 cm and height is 8 cm.
2. A parallelogram has sides 12 cm and 9 cm. If the distance between its shorter sides is 8 cm, find the distance between its longer side.
Solution:
Adjacent sides of parallelogram = 2 cm and 9 cm
Distance between shorter sides = 8 cm
Area of parallelogram = b × h
= 9 × 8 cm²
= 72 cm²
Again, area of parallelogram = b × h
⇒ 72 = 12 × h
⇒ h = 72/12
⇒ h = 6 cm
Therefore, the distance between its longer side = 6 cm.
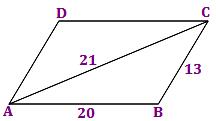
3. ABCD is a parallelogram in which AB = 20 cm, BC = 13 cm, AC = 21 cm. Find the area of parallelogram ABCD.
Solution:
Area of parallelogram ABCD = 2 area of ∆ABC
In ∆ ABC,
AB = 20 cm BC = 13 cm AC = 21 cm
So, s = (20 + 15 + 21)/2
= 54/2
= 27
Therefore, area of ∆ABC = √(27 (27 - 20) (27 - 13) (27 - 21))
= √(27 × 7 × 14 × 6)
= √(3 × 3 × 3 × 7 × 2 × 7 × 2 × 3)
= 2 × 3 × 3 × 7
= 126 cm²
Area of parallelogram ABCD = 2 area of ∆ABC
= 2 × 126 cm²
= 252 cm²
The detailed explanations on the formula of perimeter and area of parallelogram are explained above with the step-by-step solution.
● Mensuration
Perimeter and Area of Rectangle
Area and Perimeter of the Triangle
Area and Perimeter of the Parallelogram
Circumference and Area of Circle
Practice Test on Area and Perimeter of Rectangle
Practice Test on Area and Perimeter of Square
● Mensuration - Worksheets
Worksheet on Area and Perimeter of Rectangles
Worksheet on Area and Perimeter of Squares
Worksheet on Circumference and Area of Circle
Worksheet on Area and Perimeter of Triangle
7th Grade Math Problems
8th Grade Math Practice
From Area of Parallelogram to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.