Area of the Path

Here we will discuss about area of the path. It is observed that in square or rectangular gardens, parks, etc., some space in the form of path is left inside or outside or in between as cross paths. We will apply this concept for the areas of rectangle and square to determine the areas of different paths.

Worked-out examples on Area of the Path:

1. A rectangular lawn of length 50 m and breadth 35 m is to be surrounded externally by a path which is 2 m wide. Find the cost of turfing the path at the rate of $3 per m².

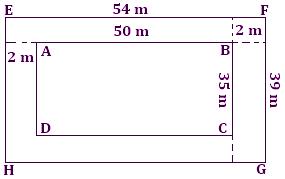
Solution: 

Length of the lawn = 50 m 

Breadth of the lawn = 35 m

Area of the lawn = (50 × 35) m²

                           = 1750 m²

Length of lawn including the path = [50 + (2 + 2)] m = 54 cm 

Breadth of the lawn including the path = [35 + (2 + 2)] m = 39 m

Area of the lawn including the path = 54 × 39 m² = 2106 m²

Therefore, area of the path = (2106 - 1750) m² = 356 m²

For 1 m², the cost of turfing the path = $ 3

For 356 m², the cost of turfing the path = $3 × 356 = $1068

2. A painting is painted on a cardboard 19 cm and 14 cm wide, such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.

Solution:

Length of the cardboard = 19 cm

Breadth of the cardboard = 14 cm

Area of the cardboard = 19 × 14 cm² = 266 cm²

Length of the painting excluding the margin = [19 - (1.5 + 1.5)] cm = 16 cm

Breadth of the painting excluding the margin = 14 - (1.5 + 1.5) = 11 cm

Area of the painting excluding the margin = (16 × 11) cm² = 176 cm²

Therefore, area of the margin = (266 - 176) cm² = 90 cm²

3. A square flowerbed is surrounded by a path 10 cm wide around it. If the area of the path is 2000 cm², find the area of the square flower-bed.

Solution:

In the adjoining figure,

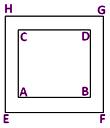
ABCD is the square flowerbed.

EFGH is the outer boundary of the path.

Let each side of the flowerbed = x cm

Then, the area of the square flowerbed ABCD (x × x) cm² = x² cm²

Now, the side of the square EFGH = (x + 10 + 10) cm = (x + 20) cm

So, the area of square EFGH = (x + 20) (x + 20) cm² = (x + 20)² cm²

Therefore, area of the path = Area of EFGH - Area of ABCD

                                            = [(x + 20)² - x²] cm²

                                            = [x² + 400 + 40x - x²] cm² = (40x + 400) cm²

But the area of path given = 2000 cm²

Therefore, 40x + 400 = 2000

⟹ 40x = 2000 - 400 

⟹ 40x = 1600

⟹     x = 1600/40 = 40

Therefore, side of square flowerbed =40 cm

Therefore, the area of the square flowerbed = 40 × 40 cm² = 1600 cm²

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Area of the Path to HOME PAGE