Area and Perimeter

Here we will learn about how to find area and perimeter of a plane figures. The perimeter is used to measure the boundaries and the area is used to measure the regions enclosed.

Perimeter:

The length of the boundary of a closed figure is called the perimeter of the plane figure. The units of perimeter are same as that of length, i.e., m, cm, mm, etc.


Area:

A part of the plane enclosed by a simple closed figure is called a plane region and the measurement of plane region enclosed is called its area.

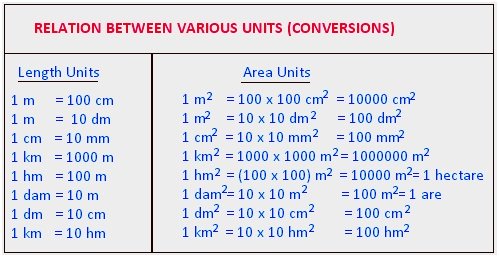
Area is measured in square units.

The units of area and the relation between them is given below: 

The different geometrical shapes formula of area and perimeter with examples are discussed below:

Perimeter and Area of Rectangle:

● The perimeter of rectangle = 2(l + b).

● Area of rectangle = l × b; (l and b are the length and breadth of rectangle)

● Diagonal of rectangle = √(l² + b²)

Perimeter and Area of the Square:

● Perimeter of square = 4 × S.

● Area of square = S × S.

● Diagonal of square = S√2; (S is the side of square)

Perimeter and Area of the Triangle:

● Perimeter of triangle = (a + b + c); (a, b, c are 3 sides of a triangle)

● Area of triangle = √(s(s - a) (s - b) (s - c)); (s is the semi-perimeter of triangle)

● S = 1/2 (a + b + c)

● Area of triangle = 1/2 × b × h; (b base , h height)

● Area of an equilateral triangle = (a²√3)/4; (a is the side of triangle)

Perimeter and Area of the Parallelogram:

● Perimeter of parallelogram = 2 (sum of adjacent sides)

● Area of parallelogram = base × height

Perimeter and Area of the Rhombus:

● Area of rhombus = base × height

● Area of rhombus = 1/2 × length of one diagonal × length of other diagonal

● Perimeter of rhombus = 4 × side

Perimeter and Area of the Trapezium:

● Area of trapezium = 1/2 (sum of parallel sides) × (perpendicular distance between them)
                                = 1/2 (p₁ + p₂) × h (p₁, p₂ are 2 parallel sides)

Circumference and Area of Circle:

● Circumference of circle = 2πr
                                        = πd
                       Where, π = 3.14 or π = 22/7
                                     r is the radius of circle
                                     d is the diameter of circle
● Area of circle = πr²

● Area of ring = Area of outer circle - Area of inner circle.

Word Problems on Area and Perimeter of Plane Figures:

1. Dan runs around a square field of side 20 m long. Ron runs around a rectangular field of length 30 m and breadth 10 m. Who covers more distance? Also find the difference between the areas of square field and rectangular field.

Solution:

Side of the square field = 20 m

Perimeter of the square field = 4 × length of one side

                                          = 4 × 20 m

                                          = 80 m

Distance covered by Dan = 80 m

Length of the rectangular field = 30 cm

Breadth of the rectangular field = 10 m

Perimeter of the rectangular field = 2 × (length + breadth)

                                                 = 2 × (30 m + 10 m)

                                                 = 2 × 40 m

                                                  = 80 m

Distance covered by Ron = 80 m

Hence both covered equal distance.

Area of the square field = side × side

                                  = 20 m × 20 m

                                  = 400 m$^{2}$

Area of the rectangular field = length × breadth

                                         = 30 × 10 cm

                                         = 300 m$^{2}$

Difference between the areas = Area of the square – area of the rectangle

                                           = 400 m$^{2}$ – 300 m$^{2}$

                                           = 100 m$^{2}$

2. A park with sides 20 m, 30 m, 6 m, 15 m, 15 m and 12 m is to be fenced. If the cost of fencing is $6 a metre, what is the total cost of fencing?

Solution:

Perimeter of the park = Sum of the length of sides

                               = 20 m + 30 m + 6 m + 15 m + 15 m + 12 m

                               = 98 m

The length of the fence = Perimeter of the park

                                  = 98 m

Cost of fencing 1 m = $ 6

Cost of fencing 98 m = $ 6 × 98

                               = $ 588

Questions and Answers on Area and Perimeter of Plane Figures:

1. A rectangular playground which is 100 m and 30 m broad is to be fenced with wire. How much wire is needed?

Answer: 260 m

2. Which is more? Area of a rectangular field of length 50 m and breadth 20 m or area of a square field of side 40 m.

Answer: Square

3. A field is in the form of a rectangle of length 60 m and breadth 30 m. Find the cost of fencing the field if the cost of fencing is $ 7 a metre. 

Answer: $ 1260

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Area and Perimeter to HOME PAGE