Perimeter and Area of Rectangle

The formula of perimeter and area of rectangle are explained step-by-step with solved examples.

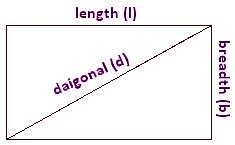
If l denotes the length and b denotes the breadth of the rectangle, then the

● Perimeter of the rectangle = 2(l + b) units

● Length of the rectangle = \(\frac{P}{2}\) - b units

● Breadth of the rectangle = \(\frac{P}{2}\) - l units

● Area of the rectangle = l × b sq. units.

● Length of the rectangle = \(\frac{A}{b}\) units .

● Breadth of the rectangle = \(\frac{A}{l}\) units

● Diagonal of the rectangle = \(\sqrt{l^{2} + b^{2}}\) units

Let us consider a rectangle of length 'a' units and breadth 'b' units.   

Therefore, perimeter of the rectangle ABCD        

                   = (AB + BC + CD + DA) units

                   = (a + b + a + b) units

                   = (2a + 2b) units

                   = 2 (a + b) units

Therefore, perimeter of the rectangle = 2 (length + breadth) units 

We know that the area of the rectangle is given by 

Area = length × breadth

A = a × b square units 

⇒ a = \(\frac{A}{b}\), i.e.,        length of the rectangle = \(\frac{Area}{breadth}\)

And b = \(\frac{A}{a}\), i.e.,     breadth of the rectangle = \(\frac{Area}{length}\)

Worked-out problems on Perimeter and Area of Rectangle: 

1. Find the perimeter and area of the rectangle of length 17 cm and breadth 13 cm. 

Solution: 

Given: length = 17 cm, breadth = 13 cm

Perimeter of rectangle = 2 (length + breadth) 

                                    = 2 (17 + 13) cm 

                                    = 2 × 30 cm  

                                    = 60 cm 

We know that the area of rectangle = length × breadth

                                                         = (17 × 13) cm\(^{2}\) 

                                                        = 221 cm\(^{2}\)

2. Find the breadth of the rectangular plot of land whose area is 660 m2 and whose length is 33 m. Find its perimeter. 

Solution: 

We know that the breadth of the rectangular plot = \(\frac{Area}{length}\)

                                                                               = \(\frac{660m^{2}}{33 m}\)

                                                                               = 20 m

Therefore, the perimeter of the rectangular plot = 2 (length + breadth) 

                                                                             = 2(33 + 20) m 

                                                                             = 2 × 53 m

                                                                             = 106 m

3. Find the area of the rectangle if its perimeter is 48 cm and its breadth is 6 cm. 

Solution:

P = 2 (l + b)

Here, P = 48 cm; b = 6 cm

Therefore, 48 = 2 (l + 6)

           ⇒ \(\frac{48}{2}\) = l + 6

           ⇒ 24 = l + 6

           ⇒ 24 - 6 = l

           ⇒ 18 = l

Therefore, length = 18 cm

Now, area of rectangle = l × b = 18 × 6 cm\(^{2}\) = 108 cm\(^{2}\)

4. Find the breadth and perimeter of the rectangle if its area is 96 cm\(^{2}\)
 and the length is 12 cm.

Solution:

Given, A = 96 cm\(^{2}\) and l = 12 cm

A = l × b

Therefore, 96 = 12 × b

            ⇒ \(\frac{96}{12}\) = b

            ⇒ b = 8 cm

Now, P = 2 (l + b)

            = 2 (12 + 8)

            = 2 × 20

            = 40 cm

5. The length and breadth of a rectangular courtyard is 75 m and 32 m. Find the cost of leveling it at the rate of $3 per m2. Also, find the distance covered by a boy to take 4 rounds of the courtyard.

Solution:

Length of the courtyard = 75 m

Breadth of the courtyard = 32 m

Perimeter of the courtyard = 2 (75 + 32) m

                                           = 2 × 107 m

                                           = 214 m

Distance covered by the boy in taking 4 rounds = 4 × perimeter of courtyard

                                                                            = 4 × 214

                                                                            = 856 m

We know that area of the courtyard = length × breadth

                                                         = 75 × 32 m\(^{2}\)

                                                         = 2400 m\(^{2}\)

For 1 m\(^{2}\), the cost of levelling = $3

For 2400 m\(^{2}\), the cost of levelling = $3 × 2400

                                                                   = $7200



Solved examples on Perimeter and Area of Rectangle:

6. A floor of the room 8 m long and 6 m wide is to be covered by square tiles. If each square tile is 0.8 m, find the number of tiles required to cover the floor. Also, find the cost of tiling at the rate of $7 per tile.

Solution:

Length of the room = 8 m

Breadth of the room = 6 m

Area of the room = 8 × 6 m\(^{2}\) {Area of room = Area of tiles that are put on the floor of the room.}

                           = 48 m\(^{2}\)

Area of one square tile = 0.8 × 0.8 m\(^{2}\) = 0.64 m\(^{2}\)

Number of tiles required = \(\frac{Area of floor}{Area of tiles}\) 

                                       = \(\frac{48}{0.64}\)

                                       = \(\frac{48 × 100}{64}\)

                                       = 75 tiles

For 1 tile, the cost of tiling is $7

For 7 tiles, the cost of tiling is $(7 × 75) = $525

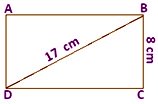
7. The breadth of the rectangle is 8 cm and A its diagonal is 17 cm. Find the area of the rectangle and its perimeter.

Solution:

Using Pythagoras theorem,

BD\(^{2}\) = DC\(^{2}\) + BC\(^{2}\)

⇒ 172 = DC\(^{2}\) + 8\(^{2}\)

⇒ 289 - 64 = DC\(^{2}\)

⇒ 225 = DC\(^{2}\)

⇒ 15 = DC

Therefore, length of rectangle = 15 cm

So, area of rectangle = l × b

                                   = 15 × 8 cm\(^{2}\)

                                   = 120 cm\(^{2}\)

Also, perimeter of rectangle = 2 (15 + 8) cm

                                             = 2 × 23 cm

                                             = 46 cm

8. The length and breadth of the rectangle park are in the ratio 5 : 4 and its area is 2420 m2, find the cost of fencing the park at the rate of $10 per metre.

Solution:

Let the common ratio b x,

then length of rectangular park = 5x

Breadth of rectangular park = 4x

Area of rectangular park = 5x × 4x

                                        = 20x\(^{2}\)

According to the question,

20x\(^{2}\) = 2420

⇒ x\(^{2}\) = \(\frac{2420}{20}\)

⇒ x\(^{2}\) = 121

⇒ x = 11

Therefore, 5x = 5 × 11 = 55 and 4x = 4 × 11 = 44

So, the perimeter of the rectangular park = 2 (l + b)

                                                                   = 2 (55 + 44)

                                                                   = 2 × 99

                                                                   = 198 cm

For 1 m, the cost of fencing = $10

For 198 m, the cost of fencing = $198 × 10

                                                 = $1980

9. How many envelopes can be made out of a sheet of paper 100 cm by 75 cm, supposing 1 envelope requires 20 cm by 5 cm piece of paper?

Solution:

Area of the sheet = 100 × 75 cm\(^{2}\) = 7500 cm\(^{2}\)

Area of envelope = 20 × 5 cm = 100 cm\(^{2}\)

Number of envelopes that can be made = \(\frac{Area of sheet}{Area of envelope}\)

                                                                = \(\frac{7500}{100}\)

                                                                = 75 envelopes

10. A wire in the shape of rectangle of length 25 cm and breadth 17 cm is rebent to form a square. What will be the measure of each side?

Solution:

Perimeter of rectangle = 2 (25 + 17) cm

                                    = 2 × 42 

                                    = 84 cm

Perimeter of square of side x cm = 4x

Therefore, perimeter of rectangle = Perimeter of Square

                                           84 cm = 4x

                                               ⇒ x = 21

Therefore, each side of square = 21 cm

These are the detailed step-by-step explanation with the formula of perimeter and area of rectangle.

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Perimeter and Area of Rectangle to HOME PAGE