Area and Perimeter of the Triangle

Here we will discuss about the area and perimeter of the triangle.

● If a, b, c are the sides of the triangle, then the perimeter of triangle = (a + b + c) units.

● Area of the triangle = √(s(s - a) (s - h) (s - c)) 

The semi-perimeter of the triangle, s = (a + b + c)/2

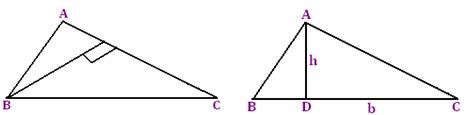
● In a triangle if 'b' is the base and h is the height of the triangle then

Area of triangle = 1/2 × base × height

Similarly,

                              1/2 × AC × BD                              1/2 × BC × AD

● Base of the triangle = (2 Area)/height 

● Height of the triangle = (2 Area)/base 

Area of right angled triangle

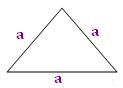
● If a represents the side of an equilateral triangle, then its area = (a²√3)/4 

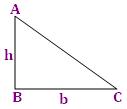
● Area of right angled triangle

A = 1/2 × BC × AB

   = 1/2 × b × h

Worked-out examples on area and perimeter of the triangle:

1. Find the area and height of an equilateral triangle of side 12 cm. (√3 = 1.73).

Solution: 

Area of the triangle = $\frac{√3}{4}$ a² square units 

= $\frac{√3}{4}$ × 12 × 12 

= 36√3 cm²

= 36 × 1.732 cm² 

= 62.28 cm²

Height of the triangle = $\frac{√3}{2}$ a units

= $\frac{√3}{2}$ × 12 cm 

= 1.73 × 6 cm 

= 10.38 cm 

2. Find the area of right angled triangle whose hypotenuse is 15 cm and one of the sides is 12 cm. 

Solution: 

AB² = AC² - BC² 

       = 15² - 12² 

       = 225 - 144

        = 81

Therefore, AB = 9

Therefore, area of the triangle = ¹/₂ × base × height

                                                 = ¹/₂ × 12 × 9 

                                                 = 54 cm²

3. The base and height of the triangle are in the ratio 3 : 2. If the area of the triangle is 243 cm² find the base and height of the triangle. 

Solution: 

Let the common ratio be x 

Then height of triangle = 2x 

And the base of triangle = 3x

Area of triangle = 243 cm²

Area of triangle = 1/2 × b × h 243 = 1/2 × 3x × 2x 

⇒ 3x² = 243

⇒ x² = 243/3

⇒ x = √81

⇒ x = √(9 × 9) 

⇒ x = √9

Therefore, height of triangle = 2 × 9 

                                             = 18 cm 

Base of triangle = 3x 

                          = 3 × 9 

                          = 27 cm

4. Find the area of a triangle whose sides are 41 cm, 28 cm, 15 cm. Also, find the length of the altitude corresponding to the largest side of the triangle. 

Solution: 

Semi-perimeter of the triangle = (a + b + c)/2

                                                 = (41 + 28 + 15)/2 

                                                 = 84/2 

                                                 = 42 cm

Therefore, area of the triangle = √(s(s - a) (s - b) (s - c)) 

                                                 = √(42 (42 - 41) (42 - 28) (42 - 15)) cm²

                                                 = √(42 × 1 × 27 × 14) cm²

                                                 = √(3 × 3 × 3 × 3 × 2 × 2 × 7 × 7) cm²

                                                 = 3 × 3 × 2 × 7 cm²

                                                 = 126 cm²

Now, area of triangle = 1/2 × b × h 

Therefore, h = 2A/b

                     = (2 × 126)/41

                     = 252/41

                     = 6.1 cm

More solved examples on area and perimeter of the triangle:

5. Find the area of a triangle, two sides of which are 40 cm and 24 cm and the perimeter is 96 cm.

Solution:

Since, the perimeter = 96 cm

a = 40 cm, b = 24 cm

Therefore, C = P - (a + b)

                     = 96 - (40 + 24)

                     = 96 - 64

                     = 32 cm

Therefore, S = (a + b + c)/2

                     = (32 + 24 + 40)/2

                     = 96/2

                     = 48 cm

Therefore, area of triangle = √(s(s - a) (s - b) (s - c))

                                           = √(48 (48 - 40) (48 - 24) (48 - 32))

                                           = √(48 × 8 × 24 × 16 )

                                           = √(2 × 2 × 2 × 2 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 2 × 2 × 2 × 2)

                                           = 3 × 2 × 2 × 2 × 2 × 2 × 2 × 2

                                           = 384 cm²

6. The sides of the triangular plot are in the ratio 2 : 3 : 4 and the perimeter is 180 m. Find its area.

Solution:

Let the common ratio be x,

then the three sides of triangle are 2x, 3x, 4x

Now, perimeter = 180 m

Therefore, 2x + 3x + 4x = 180

⇒ 9x = 180

⇒ x = 180/9

⇒ x = 20

Therefore, 2x = 2 × 20 = 40

3x = 3 × 20 = 60

4x = 4 × 20 = 80

Area of triangle = √(s(s - a) (s - b) (s - c))

                          = √(90(90 - 80) (90 - 60) (90 - 40))

                          = √(90 × 10 × 30 × 50))

                          = √(3 × 3 × 2 × 5 × 2 × 5 × 3 × 2 × 5 × 5 × 5 × 2)

                          = 3 × 2 × 5 × 2 × 5 √(3 × 5)

                          = 300 √15 m²

                          = 300 × 3.872 m²

                          = 1161.600 m²

                          = 1161.6 m²

The above explanation on area and perimeter of the triangle are explained using step-by-step solution.

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Area and Perimeter of the Triangle to HOME PAGE