Area of Rhombus

Here we will learn how to find the area of rhombus.

ABCD is a rhombus whose base AB = b, DB ⊥ AC   DB = d₁ AC = d₂ and the altitude from C on AB is CE, i.e., h.

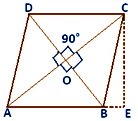
Area of rhombus ABCD   = 2 Area of ∆ ABC

                                     = 2 × 1/2 AB × CD sq units.

                                     = 2 × 1/2 b × h sq. units

                                     = base x height sq. units


Also, area of rhombus    = 4 × area of ∆ AOB

                                    = 4 × 1/2 × AO × OB sq. units

                                    = 4 × 1/2 × 1/2 d₂ × 1/2 d₁ sq. units

                                    = 4 × 1/8 d₁ × d₂ square units

                                    = 1/2 × d₁ × d₂; where d₁ and d₂ are diagonals.

Therefore, area of rhombus = 1/2 (product of diagonals) square units

• Perimeter of rhombus = 4 × side 

Worked-out examples on area of rhombus:

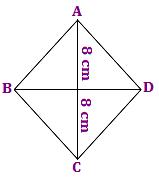
1. Find the area of the rhombus having each side equal to 17 cm and one of its diagonals equal to 16 cm.

Solution:

ABCD is a rhombus in which AB = BC = CD = DA = 17 cm
AC = 16 cm

Therefore, AO = 8 cm

In ∆ AOD,

   AD² = AO² + OD²

⇒ 17² = 8² + OD²

⇒ 289 = 64 + OD²

⇒ 225 = OD²

⇒ OD = 15

Therefore, BD   = 2 OD

                       = 2 × 15

                       = 30 cm

Now, area of rhombus

= 1/2 × d₁ × d₂

= 1/2 × 16 × 30

= 240 cm²

2. Find the altitude of the rhombus whose area is 315 cm² and its perimeter is 180 cm.

Solution:

Since, the perimeter of rhombus = 180 cm

Therefore, side of rhombus = P/4 = 180/4 = 45 cm

Now, area of rhombus = b × h

⇒ 315 = 45 × h

⇒ h = 315/45

⇒ h =7 cm

Therefore, altitude of the rhombus is 7 cm.

3. The floor of building consists of 2000 tiles which are rhombus shaped and each of its diagonals are 40 cm and 25 cm in length. Find the total cost of polishing the floor, if the cost per m² is $5.

Solution:

In each rhombus, the tile length of the diagonals = 40 cm and 25 cm

Therefore, area of each tile = 1/2 × 40 × 25 = 500 cm²

Therefore, area of 2000 tiles      = 2000 × 500 cm²

                                               = 1000000 cm²

                                               = 1000000/10000 cm²

                                               = 100 m²

For 1 m² cost of polishing = $5 = $5 × 100 = $500.

The formula of perimeter and area of rhombus are explained above with the detailed step-by-step explanation using various examples.

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Area of Rhombus to HOME PAGE