Circumference and Area of Circle

In this topic we will discuss and learn about the circumference and area of circle.

Circumference of circle: The distance around the circular region is called its circumference. The ratio of circumference of any circle to its diameter is constant. This constant is denoted by π and is read as pie.

Circumference/Diameter = Pie

i.e., c/d = π   or   c = πd

We know that diameter is twice the radius, i.e., d = 2r

    C = π × 2r

⇒ C = 2πr

Therefore approximate value of π = 22/7 or 3.14.

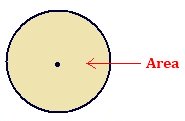
Area of circle: The measure of the region enclosed inside the circle is called its area. 

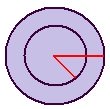
In case of concentric circles: The region enclosed between two concentric circles of different radii is called the area of the ring.

Note: 

Circles having same centre but different radii are called concentric circles. 

Worked-out examples on how do you find the area of a circle and the circumference of circle: 

1. Find the circumference and area of radius 7 cm.

Solution:

Circumference of circle = 2πr

                                     = 2 × 22/7 × 7

                                     = 44 cm

Area of circle = πr²

                      = 22/7 × 7 × 7 cm²

                      = 154 cm²

2. A race track is in the form of a ring whose inner circumference is 220 m and outer circumference is 308 m. Find the width of the track.

Solution:

Let r₁ and r₂ be the outer and inner radii of ring.

Then 2πr₁ = 308

2 × 22/7 r₁ = 308

⇒ r₁ = (308 × 7)/(2 × 22)

⇒ r₁ = 49 m

2πr₂ = 220

⇒ 2 × 22/7 × r₂ = 220

⇒ r₂ = (220 × 7)/(2 × 22) 

⇒ r₂ = 35 m 

Therefore, width of the track = (49 - 35) m = 14 m

3. The area of a circle is 616 cm². Find its circumference.

Solution:

We know area of circle = πr²

⇒ 22/7 × r² = 616

⇒ r² = (616 × 7)/22

⇒ r² = 28 × 7

⇒ r = √(28 × 7)

⇒ r = √(2 × 2 × 7 × 7)

⇒ r = 2 × 7

⇒ r = 14 cm

Therefore, circumference of circle = 2πr

                                                       = 2 × 22/7 × 14

                                                       = 88 cm

4. Find the area of the circle if its circumference is 132 cm.

Solution:

We know that the circumference of circle = 2πr

Area of circle = πr²

Circumference = 2πr = 132

⇒ 2 × 22/7 × r = 132

⇒ r = (7 × 132)/(2 × 22)

⇒ r = 21 cm

Therefore, area of circle = πr²

                                       = 22/7 × 21 × 21

                                       = 1386 cm²

5. The ratio of areas of two wheels is 25 : 49. Find the ratio of their radii.

Solution:

If A₁ and A₂ are the area of wheels,

A₁/A₂ =25/49

⇒ (πr₁²)/(πr₂²) = 25/49 

⇒ (r₁²)/(r₂²) = 25/49 

⇒ r₁/r₂ = √(25/49) 

⇒ r₁/r₂ = 5/7 

Therefore, ratio of their radii is 5 : 7.

6. The diameter of a wheel of a motorcycle is 63 cm. How many revolutions will it make to travel 99 km?

Solution:

The diameter of the wheel of a motorcycle = 63 cm

Therefore, circumference of the wheel of motorcycle = πd

                                                                                    = 22/7 × 63

                                                                                    = 198 cm

Total distance travelled by motorcycle = 99 km

                                                              = 99 × 1000

                                                              = 99 × 1000 × 100 cm

Therefore, number of revolutions = (99 × 1000 × 100)/198 = 50000

7. The diameter of a wheel of cycle is 21 cm. It moves slowly along a road. How far will it go in 500 revolutions?

Solution:

In revolution, distance that wheel covers = circumference of wheel Diameter of wheel = 21 cm

Therefore, circumference of wheel = πd

                                                        = 22/7 × 21

                                                        = 66 cm

So, in 1 revolution distance covered = 66 cm

In 500 revolution distance covered = 66 × 500 cm

                                                        = 33000 cm

                                                        = 33000/100 m

                                                        = 330 m

8. The circumference of a circle exceeds the diameter by 20 cm. Find the radius of the circle.

Solution:

Let the radius of circle of = r m.

Then circumference = 2 πr

Since, circumference exceeds diameter by 20

Therefore, according to question;

2 πr = d + 20

⇒ 2 πr = 2r + 20 

⇒ 2 × (22/7) × r = 2r + 20

⇒ 44r/7 - 2r = 20

⇒ (44r - 14r)/7 = 20

⇒ 30r/7 = 20 

⇒ r = (7 × 20)/30

⇒ r =14/3

So, the radius of circle = 14/3 cm = 42/3 cm

9. A piece of wire in the form of rectangle 40 cm long and 26 cm wide is again bent to form a circle. Find the radius of the circle.

Solution:

Length of wire = Perimeter of rectangle

                        = 2(l + b)

                        = 2(40 + 26)

                        = 2 × 66

                        = 132 cm

When it is again bent to form a circle, then

Perimeter of circle = Perimeter of rectangle

2 πr = 132 cm

⇒ 2 × 22/7 × r = 132

⇒ r = (132 × 7)/(2 × 22) 

⇒ r = 21 cm

Formula is used to solve the different examples on circumference and area of circle with the detailed step-by-step explanation.

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhombus

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Practice Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Square

● Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Area of Circle

Worksheet on Area and Perimeter of Triangle

7th Grade Math Problems

8th Grade Math Practice

From Circumference and Area of Circle to HOME PAGE