Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition of Integers
We will learn addition of integers using number line.
We know that counting forward means addition.
Having learnt how to add two whole numbers on the number line, we shall extend the same method for addition of integers using the number line. The only difference is the when adding a negative integer, the moves are made to the left.
Working Rules for Addition of Integers:
Step I: Draw a number line and mark points as negative integers.
i.e., (..., -4, -3, -2, -1,), zero and positive integers i.e., (1, 2, 3, 4, ...)
Step II: For a positive integer move forward and for a negative integer move backward.
Step III: The end is the result.
Addition of Two Positive Integers:
When we add positive integers, we move to the right on the number line.
For example to add +2 and +4 we move 4 steps to the right of +2.
Thus, +2 +4 = +6.
Addition of Two Negative Integers:
When we add two negative integers, we move to the left on the number line.
For example to add -2 and -4 we move 4 steps to the left of -2.
Thus, -2 + (-4) = -6.
Addition of a Negative Integer and a Positive Integer:
When a negative integer is added to a positive integer we move to the left on the number line.
For example to add +2 + (-4), we move 4 steps to the left of +2.
Thus, +2 + (-4) = -2.
Addition of a Positive Integer and a Negative Integer:
When a positive integer is added to a negative integer we move to the right on the number line.
For example to add (-6) + 3, we move 3 steps to the right of -6.
Thus, (-6) + 3 = -3.
We can add two integers having same sings by adding their absolute values and placing the common sign of two integers before it.
Solved Examples on Addition of Integers:
1. Find the value +18 + (+5)
Solution:
Absolute value of |+18| = 18
Absolute value of |+5| = 5
Sum of absolute values = 18 + 5
Since, both integers have common sign +, we place + sign in the answer.
Hence, +18 + (+5) = +23.
We can add two integers having opposite signs by finding difference of their absolute values and placing the sign of the integer with the greater absolute value before it.
2. Find the value -38 + (+28)
Solution:
Absolute value of |-38| = 38
Absolute value of |+28| = 28
Difference of absolute values = 38 – 28 = 10
Placing the sign of the integer with the greater absolute value = -10
Hence, -38 + (+28) = -10.
3. Using the number line, find the following.
(i) 3 + 4
(ii) (-3) + 5
(iii) 3 + (-5)
Solution:
(i) 3 + 4
Start from 3 and proceed 4 units to the right to reach point P. which represents 7.
Hence, 3 + 4 = 7.
(ii) (-3) + 5
Start from -3 and proceed 5 units to the right to reach point P. which represents 2.
Hence, (-3) + 5 = 2
(iii) 3 + (-5)
Start from 3 and move 5 units to the left to reach point P, which represents -2.
Hence 3 + (-5) = -2.
4. Add the following numbers or number line:
(i) 5 and 3
(ii) -2 and -3
(iii) 5 and -3
Solution:
(i) 5 and 3
Hence, 5 + 3 = 8
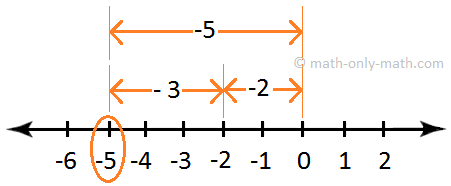
(ii) -2 and -3
Hence, -2 + (-3) = -5
(iii) 5 and -3
Hence, 5 + (-3) = -5
5. Add 5 and 3 on the number line.
Solution:
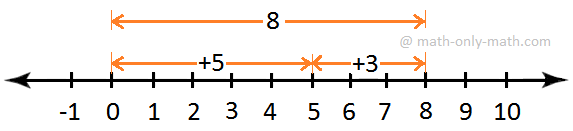
On the number line, start from and move 5 units to the right to reach point P. which represents 5.
Now start from P and move 3 units to the right of P to reach point Q.
Clearly, Q represents 8
Hence, 5 + 3 = 8.
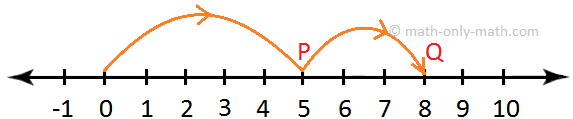
6. Add 7 and -3 on the number line.
Solution:
On the number line, start from 0 and move 7 units to the right to reach point P, which represents 7.
Now start from P and move 3 units to the left of A to reach point Q.
Clearly, Q represents 4.
Hence, 7 + (-3) = 4.
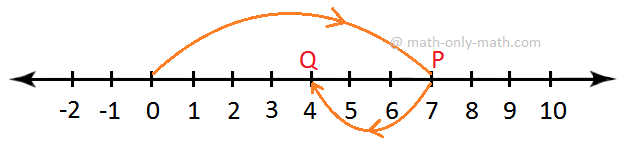
7. Add -3 and -5 on the number line.
Solution:
On the number line, start from 0 and move 3 units to the left to reach point P, which represents -3. Now start from P and move 5 units to the left of P to reach point Q.
Clearly, Q represents -8.
Hence, (-3) + (-5) = -8.
5th Grade Numbers Page
5th Grade Math Problems
From Addition of Integers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
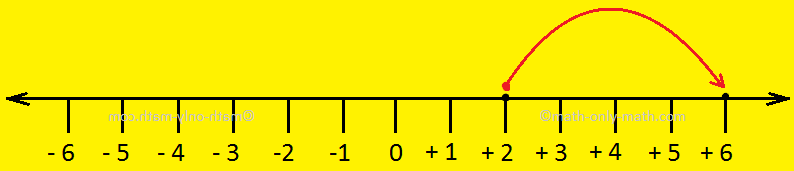
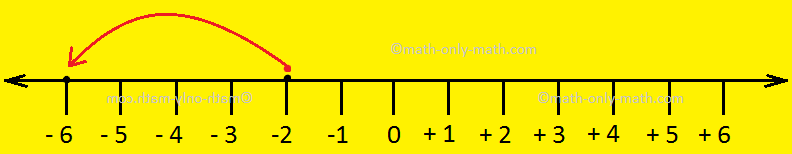




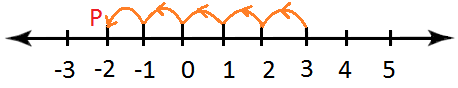
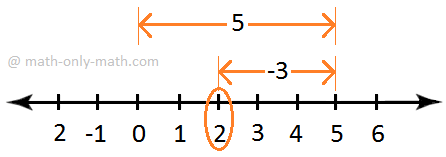
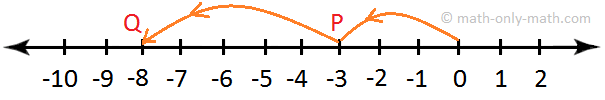


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.