Subscribe to our YouTube channel for the latest videos, updates, and tips.
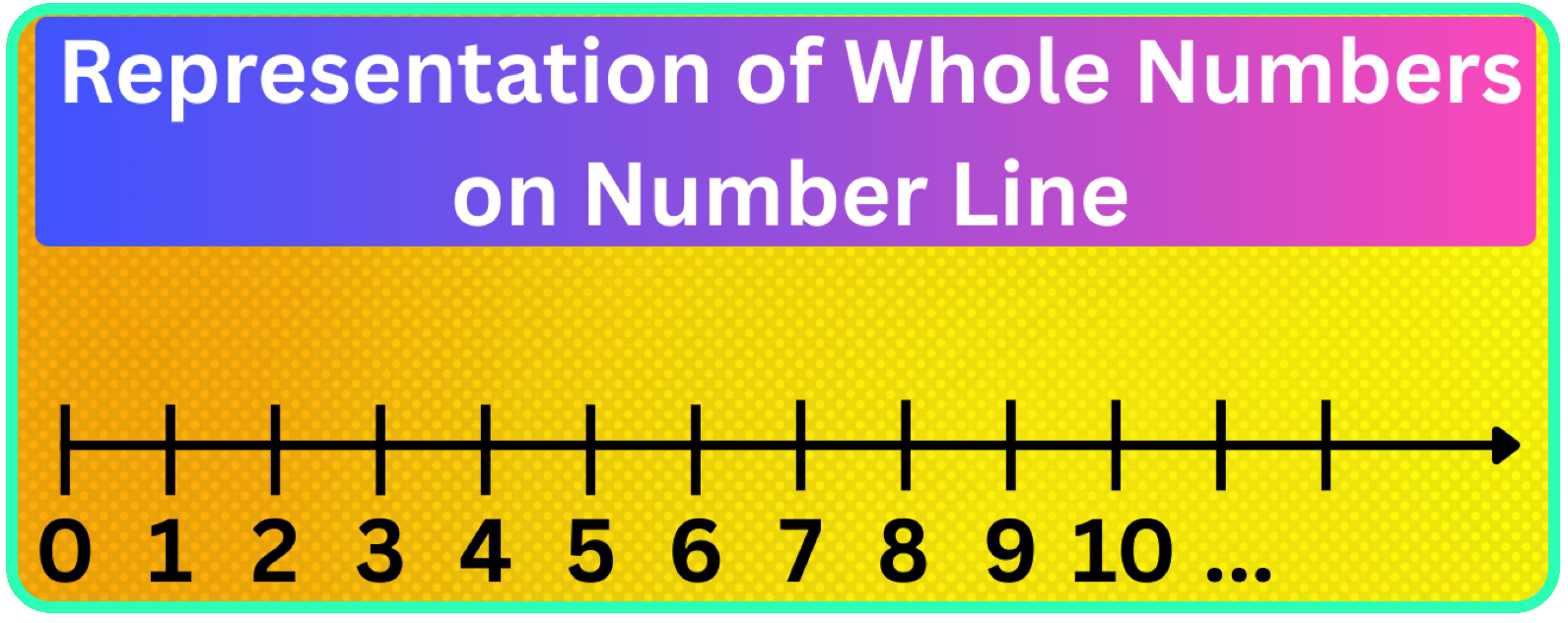
Representation of Whole Numbers on Number Line
Numbers on a line is called the representation of whole numbers on number line.
The number line also helps us to compare two whole numbers, i.e., to decide which of the two given whole numbers is greater or smaller.
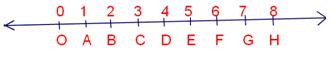
In order to represent whole numbers on a number line, we draw a straight line and mark a point O on it.
Starting from O, mark points A, B, C, D, E, F, G, H, etc. on the line at equal distances to the right of O.
Label the point O as 0.
Let us take OA = 1 unit. Then, AB = BC = CD = DE = 1 unit.
Now,
OB = OA + AB = (1 + 1) units = 2 units,
OC = OB + BC = (2 + 1) units = 3 units,
OD= OC + CD = (3 + 1) units = 4 units and so on.
Since O corresponds to the whole number 0, therefore, A, B, C, D, etc. correspond to the whole numbers 1, 2, 3, 4, etc. respectively.
The arrow marks on both ends of the line indicate that the number line extends indefinitely on both sides.
The following number line represents a whole number line on which whole numbers a represented.
The distance between two points (labelled 0 and 1) is called unit distance.
Step I: Draw a line and mark a point on it. Label the point as O.
Step II: Starting from O, mark off points A, B, C, D, E, F, G etc. to the right of O at equal intervals.
Taking OA = 1 unit, we get AB = BC = CD = DE = EF = FG = 1 unit
Now OB = OA + AB = (1 + 1) units = 2 units
OC = OA + AB + BC = (1 + 1 + 1) units = 3 units
OD = OA + AB + BC + CD = (1 + 1 + 1 + 1) units = 4 units and so on.
Since O represents the whole number zero, therefore A, B, C, D, E, F, G, etc. represent the whole numbers 1, 2, 3, 4, 5, 6, 7, etc., respectively.
So on the given number line, 1, 2, 3, 4, 5, 6, 7 ... are written against A, B, C, D, E, F, G..., respectively.
Similarly, every whole number can be represented by some point on the number line.
Representation of Whole Numbers on Number Line
Division as The Inverse of Multiplication
You might like these
Counting Natural Numbers | Definition of Natural Numbers | Counting
Natural numbers are all the numbers from 1 onwards, i.e., 1, 2, 3, 4, 5, …... and are used for counting. We know since our childhood we are using numbers 1, 2, 3, 4, 5, 6, ………..
Reading and Writing Large Numbers | Large Numbers in Words in Billion
In reading and writing large numbers we group place values into periods ‘ones or unit’, ‘tens’, ‘hundred’, ‘thousand’, ‘10 thousand’, ‘100 thousand’, ‘million’, ’10 million’, ‘100 million
Numbers | Notation | Numeration | Numeral | Estimation | Examples
Numbers are used for calculating and counting. These counting numbers 1, 2, 3, 4, 5, .......... are called natural numbers. In order to describe the number of elements in a collection with no objects
Properties of Addition | Identity, Commutative, Associative, Additive
The properties of addition whole numbers are as follows: Closure property: If a and b are two whole numbers, then a + b is also a whole number. In other words, the sum of any two whole numbers i
Estimating Sum and Difference | Reasonable Estimate | Procedure | Math
The procedure of estimating sum and difference are in the following examples. Example 1: Estimate the sum 5290 + 17986 by estimating the numbers to their nearest (i) hundreds (ii) thousands.
Estimating Product and Quotient |Estimated Product |Estimated Quotient
The procedure of estimating product and quotient are in the following examples. Example 1: Estimate the product 958 × 387 by rounding off each factor to its greatest place.
Properties of Whole Numbers | Closure Property | Commutative Property
The properties of whole numbers are as follows: The number 0 is the first and the smallest whole numbers. • All natural numbers along with zero are called whole numbers.
Properties of Subtraction |Whole Numbers |Subtraction of Whole Numbers
1. When zero is subtracted from the number, the difference is the number itself. For example, 8931 – 0 = 8931, 5649 – 0 = 5649 2. When a number is subtracted from itself the difference is zero. For example, 5485 – 5485 = 0 3. When 1 is subtracted from a number, we get its
Whole Numbers | Definition of Whole Numbers | Smallest Whole Number
The whole numbers are the counting numbers including 0. We have seen that the numbers 1, 2, 3, 4, 5, 6……. etc. are natural numbers. These natural numbers along with the number zero
Addition of Numbers using Number Line | Addition Rules on Number Line
Addition of numbers using number line will help us to learn how a number line can be used for addition. Addition of numbers can be well understood with the help of the number line.
Subtraction of Numbers using Number Line |Subtracting with Number Line
Subtraction of numbers using number line will help us to learn how a number line can be used for subtracting one number from the another number.
Worksheet on Reading and Writing Large Numbers|Writing Numbers in Word
Practice the questions given in the worksheet on reading and writing large numbers to group place values into periods in hundred, thousand, million and billion. The questions are related to writing
Worksheet on Estimation | Estimate the Product |Nearest Tens, Hundreds
Practice the questions given in the worksheet on estimation. The questions are based on estimating the sum, difference, product and quotient to the nearest tens, hundreds and thousands.
Properties of Adding Integers | Closure |Commutative | Associative ...
The properties of adding integers are discussed here along with the examples. 1. The addition (sum) of any two integers is always an integer. For example: (i) 5 + 9 = 14 ∈ Z (ii) (-5) + 9 = 4 ∈ Z
Subtracting Integers | Subtraction of Integers |Fundamental Operations
Subtracting integers is the second operations on integers, among the four fundamental operations on integers. Change the sign of the integer to be subtracted and then add.
6th Grade Page
From Representation of Whole Numbers on Number Line to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
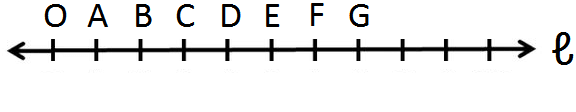
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.