Addition of Numbers using Number Line
Addition of numbers using number line will help us to learn how a number line can be used for addition.
Addition of numbers can be well understood with the help of the number line. Keep in mind the following rules of movements on the number line.
(i) In order to add a positive number, we move the same number of steps to the right on the number line as the value of the number.
(ii) In order to add a negative number, we move the same number of steps to the left on the number line as the value of the number.
Addition of numbers using number line in different situation:
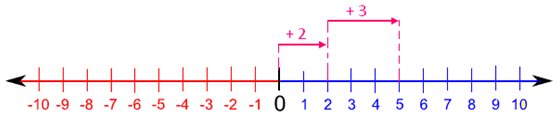
1. Addition of a positive number to a positive number,
For example: (+2) + (+3)
First of all, for +2, count 2 units to the right of zero (because right side is for the positive sign). Then for +3 move three units to the right of +2. Thus, we reach at +5.
Therefore, (+2) + (+3) = +5 or simply we can write, 5.
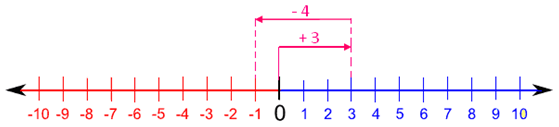
2. Addition of a positive number to a negative number,
For example: (+3) + (-4).
For +3, move 3 units to the right of zero and then for -4, move 4 units to the left of 3.
Thus, we reach at -1.
Therefore (+3) + (-4) = -1.
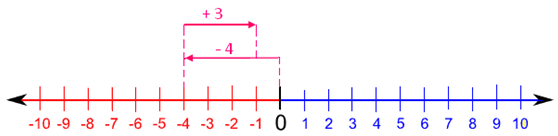
3. Addition of a negative number to a positive number,
For example: (-4) + (+3)
For -4, move 4 units to the left of zero and then for +3, move 3 units to the right of -4.
Thus, we reach at -1.
Therefore (-4) + (+3) = -1.
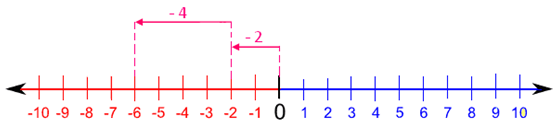
4. Addition of a negative number to a negative number,
For example: (-2) + (-4)
For -2, start from zero and move two units to the left and then again for -4, move 4 units to the left of -2. Thus, we reach at -6.
Therefore (-2) + (-4) = -6.
Addition of Whole Numbers on Number Line
We already known that addition means putting things together.
Addition of whole numbers can be shown on a number line.
1. Let us see the addition of 3 and 4.
The point at the tip of the leftmost arrow is 3. Start from 3. Since we add 4 to this number, we make 4 jumps to the right ie.. from 3 to 4, 4 to 5, 5 to 6 and 6 to 7 as shown above the tip of the rightmost arrow in the fourth jump is at 7.
Hence, sum of 3 and 4 is 7 i.c., 3 + 4 = 7.
2. Using the number line, write the whole number which is the sum of 5 and 4.
The point at the tip of the leftmost arrow is 5.
To find the sum of 5 and 4, start from 5 and proceed 4 units to the right to obtain the required result, i.e., 9, as shown in the following figure.
Hence, 5 + 4 = 9
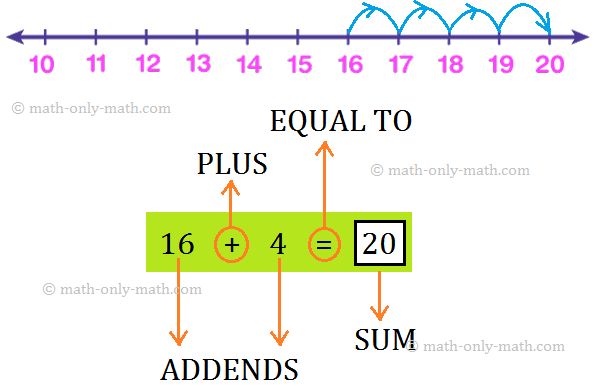
3. Let us add 16 and 4 on the number line.
To add 16 and 4 on the number line, we start from 16 and count 4 steps forward.
16 + 4 = 20
You might like these
Counting Natural Numbers | Definition of Natural Numbers | Counting
Natural numbers are all the numbers from 1 onwards, i.e., 1, 2, 3, 4, 5, …... and are used for counting. We know since our childhood we are using numbers 1, 2, 3, 4, 5, 6, ………..
Reading and Writing Large Numbers | Large Numbers in Words in Billion
In reading and writing large numbers we group place values into periods ‘ones or unit’, ‘tens’, ‘hundred’, ‘thousand’, ‘10 thousand’, ‘100 thousand’, ‘million’, ’10 million’, ‘100 million
Numbers | Notation | Numeration | Numeral | Estimation | Examples
Numbers are used for calculating and counting. These counting numbers 1, 2, 3, 4, 5, .......... are called natural numbers. In order to describe the number of elements in a collection with no objects
Properties of Addition | Identity, Commutative, Associative, Additive
The properties of addition whole numbers are as follows: Closure property: If a and b are two whole numbers, then a + b is also a whole number. In other words, the sum of any two whole numbers i
Estimating Sum and Difference | Reasonable Estimate | Procedure | Math
The procedure of estimating sum and difference are in the following examples. Example 1: Estimate the sum 5290 + 17986 by estimating the numbers to their nearest (i) hundreds (ii) thousands.
Estimating Product and Quotient |Estimated Product |Estimated Quotient
The procedure of estimating product and quotient are in the following examples. Example 1: Estimate the product 958 × 387 by rounding off each factor to its greatest place.
Properties of Whole Numbers | Closure Property | Commutative Property
The properties of whole numbers are as follows: The number 0 is the first and the smallest whole numbers. • All natural numbers along with zero are called whole numbers.
Representation of Whole Numbers on Number Line | Compare Whole Numbers
Numbers on a line is called the representation of whole numbers on number line. The number line also helps us to compare two whole numbers, i.e., to decide which of the two given whole numbers
Properties of Subtraction |Whole Numbers |Subtraction of Whole Numbers
1. When zero is subtracted from the number, the difference is the number itself. For example, 8931 – 0 = 8931, 5649 – 0 = 5649 2. When a number is subtracted from itself the difference is zero. For example, 5485 – 5485 = 0 3. When 1 is subtracted from a number, we get its
Whole Numbers | Definition of Whole Numbers | Smallest Whole Number
The whole numbers are the counting numbers including 0. We have seen that the numbers 1, 2, 3, 4, 5, 6……. etc. are natural numbers. These natural numbers along with the number zero
Subtraction of Numbers using Number Line |Subtracting with Number Line
Subtraction of numbers using number line will help us to learn how a number line can be used for subtracting one number from the another number.
Worksheet on Reading and Writing Large Numbers|Writing Numbers in Word
Practice the questions given in the worksheet on reading and writing large numbers to group place values into periods in hundred, thousand, million and billion. The questions are related to writing
Worksheet on Estimation | Estimate the Product |Nearest Tens, Hundreds
Practice the questions given in the worksheet on estimation. The questions are based on estimating the sum, difference, product and quotient to the nearest tens, hundreds and thousands.
Properties of Adding Integers | Closure |Commutative | Associative ...
The properties of adding integers are discussed here along with the examples. 1. The addition (sum) of any two integers is always an integer. For example: (i) 5 + 9 = 14 ∈ Z (ii) (-5) + 9 = 4 ∈ Z
Subtracting Integers | Subtraction of Integers |Fundamental Operations
Subtracting integers is the second operations on integers, among the four fundamental operations on integers. Change the sign of the integer to be subtracted and then add.
From Addition of Numbers using Number Line to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Least Common Factor (LCM) | Factorization & Division Method
Mar 25, 25 02:39 AM
We already familiar with the least common multiple which is the smallest common multiple of the numbers. The least (lowest) common multiple of two or more numbers is exactly divisible by each of the g… -
5th Grade Highest Common Factor | HCF | GCD|Prime Factorization Method
Mar 24, 25 11:58 PM
The highest common factor (H.C.F.) of two or more numbers is the highest or greatest common number or divisor which divides each given number exactly. Hence, it is also called Greatest Common Divisor… -
5th Grade Factors and Multiples | Definitions | Solved Examples | Math
Mar 23, 25 02:39 PM
Here we will discuss how factors and multiples are related to each other in math. A factor of a number is a divisor which divides the dividend exactly. A factor of a number which is a prime number is… -
Adding 2-Digit Numbers | Add Two Two-Digit Numbers without Carrying
Mar 23, 25 12:43 PM
Here we will learn adding 2-digit numbers without regrouping and start working with easy numbers to get acquainted with the addition of two numbers. -
Worksheet on 12 Times Table | Printable Multiplication Table | Video
Mar 23, 25 10:28 AM
Worksheet on 12 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.