Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Properties of Addition
The properties of addition whole numbers are as follows:
I. Closure Property of Addition:
If a and b are two whole numbers, then a + b is also a whole number. In other words, the sum of any two whole numbers is a whole number or, whole numbers are closed for addition.
Verification: In order to verify this property, let us take any two whole numbers and add them. We find that the sum is always a whole numbers as shown below
7 + 3 = 10 (10 is also a whole number)
0 + 8 = 8 (8 is also a whole number)
29 + 37 = 66 (66 is also a whole number)
II. Commutative Property of Addition / Order Property of Addition:
If a and b are any two whole numbers, then a + b = b + a.
In other words, the sum of two whole numbers remains the same even if the order of whole numbers (called addends) is changed.
The numbers can be added in any order. The sum of two numbers remains same even if the order of numbers is changed.
For example:
I. 4313 + 3142 = 7455
3142 + 4313 = 7455
Changing the order of the addends, 4313 and 3142 does not change the sum.
II. 133 + 142 = 275
142 + 133 = 275
Changing the order of the addends, 133 and 142, does not change the sum.
Verification:
In order to verify this property, let us consider some pairs of whole
numbers and add them in two different orders. We find that the sum
remains the same as shown below:
9 + 3 = 3 + 9
13 + 25 = 25 + 13
0 + 32 = 32 + 0
We can add two numbers in any order.
6 + 3 is same as 3 + 6
6 + 3 = 3 + 6
III. Existence of Additive Identity of Addition / Identity Property of Addition / Zero Property of Addition:
If a is any whole number, then
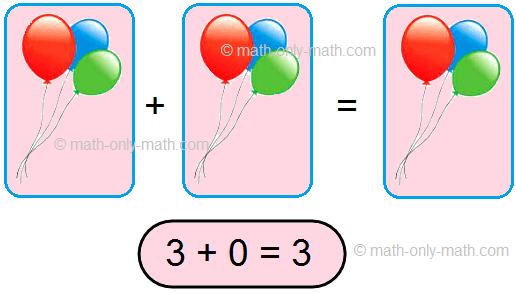
a + 0 = a = 0 + a
In other words, the sum of any whole number and zero is the number itself. That is, zero is the only whole number that does not change the value (identity) of the number it is added to.
The whole number 0 (zero) is called the additive identity or the identity element for addition of whole numbers.
The number remains the same when zero is added to the number.
For example:
I. 5918 + 0 = 5918
Identity of 5918 remains the same when added to zero.
II. 45 + 0 = 45
Identity of 45 remains same when added to zero.
Verification: In order to verify this property, we take any whole number and add it to zero. We find that the sum is the whole number itself as shown below:
5 + 0 = 5 = 0 + 5
27 + 0 = 27 = 0 + 27
137 + 0 = 137 = 0 + 137
Note:
Zero is called the additive identity because it maintains or does not change the identity (value) of the numbers during the operation of addition.
Addition of Zero:
IV. Associativity of Addition / Associative Property of Addition:
If a, b, c are any three whole numbers, then
(a + b) + c = a + (b + c)
In other words, the addition of whole numbers is associative.
When three or more numbers are added, the sum remains the same regardless of their group or place.
For example:
I. 4610 + 1129 + 2382 = 5739 + 2382 = 8121
4610 + 1129 + 2382 = 4610 + 3511 = 8121
4610 + 2382 + 1129 = 6992 + 1129 = 8121
Grouping of the addends does not change the sum.
II. 23 + 45 + 16 = 68 + 16 = 84
23 + 45 + 16 = 23 + 61 = 84
23 + 16 + 45 = 39 + 45 = 84
Grouping of the addends does not change the sum.
Verification: In order to verify this property, we take three whole numbers, say a, b, c and find the values of the expression (a + b) + c and a + (b + c). We find that the values of these expression remain same, as shown below;
(i) (2 + 5) + 7 = 2 + (5 + 7)
then, 7 + 7 = 2 + 12
14 = 14
(ii) (5 + 10) + 13 = 5 + (10 + 13)
then, 15 + 13 = 5 + 23
28 = 28
(iii) (9 + 0) + 11 = 9 + (0 + 11)
then, 9 + 11 = 9 + 11
20 = 20
Let us consider any three whole numbers a, b, c.
We have, (a + b) + c
= (b + a) + c [By using commutativity of addition we have a + b = b + a]
= b + (a + c) [By using associativity of addition]
= b + (c + a) [By using commutativity of addition]
= (b + c) + a [By using associativity of addition]
= (c + b) + a [By using commutativity of addition]
V. Property of Opposites of Addition:
For any real number a, there is a unique real number –a such that
a + (–a) = 0 and (–a) + a = 0
The sum of the real number (a) and its opposite real number (-a) is zero then they are known as the additive inverses of each other.
Verification:
5 + (-5) = 0 and (-5) + 5 = 0
or, 5 - 5 = 0 and -5 + 5 = 0
Here 5 is real number and (-5) is it's opposite real number. Sum of 5 and (-5) is zero.
Therefore, (-5) is additive inverses of 5
or, 5 is additive inverses of (-5).
VI. Property of Opposite of a Sum of Addition:
If a and b are any two whole numbers,then
–(a + b) = (–a) + (–b)
The opposite of the sum of whole numbers is equal to the sum of the opposites whole numbers.
Verification:
-(3 + 4) = (-3) + (-4)
or, -(7) = -3 -4
or, -7 = -7
Here the opposite of the sum of 3 and 4 is equal to -7.
The opposites of 3 and 4 are (-3) and (-4) respectively.
The sum of the opposites (-3) and (-4) is equal to -7.
VII. Property of Successor of a Sum / Successor Property of Addition:
If a is any whole number, then
a + 1 = (a + 1), which is a successor of "a".
If we add 1 with the sum of a number, we will have successor of the number.
On adding 1 to any number, we get the number just after it.
For example:
I. 26519 + 1 = 26520
26520 is successor of 26519
II. 276 + 1 = 277
277 is the successor of 276
Verification:
2420 + 1 = 2421
2421 is the successor of 2420.
Similarly, 1 + 2542 = 2543
2543 is the successor of 2542.
Solved Examples on Properties of Addition:
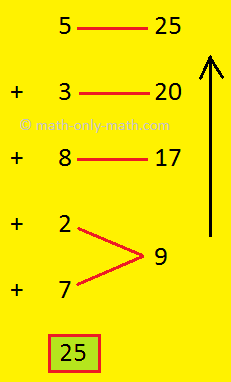
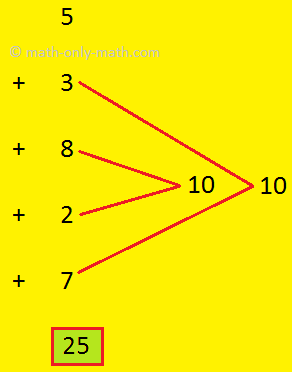
1. Find the sum of 5, 3, 8, 2 and 7.
Also 5 + 3 + 8 + 2 + 7 = 25
3 + 8 + 5 + 2 + 7 = 25
7 + 2 + 8 + 5 + 3 = 25
While adding we can change the order of addends in any way but the sum is always the same.
Worksheet on Properties of Addition:
1. What is one more than
(i) 2,271
(ii) 4,245
(iii) 6,492
(iv) 2,456
(v) 2,198
(vi) 3,040
Answer:
1. (i) 2,272
(ii) 4,246
(iii) 6,493
(iv) 2,457
(v) 2,199
(vi) 3,041
2. What is 10 more than:
(i) 3,462
(ii) 4,298
(iii) 9,011
(iv) 2,321
(v) 3,462
(vi) 2,429
Answer:
2. (i) 3,472
(ii) 4,308
(iii) 9,021
(iv) 2,331
(v) 3,472
(vi) 2,439
3. What is 100 more than:
(i) 3,721
(ii) 5,673
(iii) 7,132
(iv) 4,271
(v) 9,248
(vi) 6,475
Answer:
3. (i) 3,821
(ii) 5,773
(iii) 7,232
(iv) 4,371
(v) 9,348
(vi) 6,575
4. What is 1000 more than:
(i) 7,326
(ii) 7,125
(iii) 8,248
(iv) 5,492
(v) 4,320
(vi) 8,167
Answer:
4. (i) 8,326
(ii) 8,125
(iii) 9,248
(iv) 6,492
(v) 5,320
(vi) 9,167
5. Fill in the blanks:
(i) 2 + ____ = 2 + 3
(ii) 9 + 1 = ____ + 9
(iii) 7 + 0 = ____
(iv) 8 + 2 = 2 + ____
(v) 5 + 4 = 4 + ____
(vi) 6 + 1 = ____ + 6
Answer:
5. (i) 3
(ii) 1
(iii) 7
(iv) 8
(v) 5
(vi) 1
6. Fill the given blanks using the properties of addition.
(i) 19,94,450 + 3,07,689 = __________ + 19,94,450
(ii) 18,47,336 + __________ = 18,47,336
(iii) 11,300,999 + 1 = __________
(iv) __________ + 0 = 18,95,72,025
(v) (84,32,583 + 22,68,592) + 90,81,225 = 84,32,583 + (__________ + 90,81,225)
(vi) 37,46,442 + 20,000 = __________
(vii) 209,718,660 + 1,000,000 = __________
(i) 674 + 0 = ………….
(ii) 0 + …………. = 174
(iii) 723 + 122 = …………. + 723
(iv) 118 + 687 = 687 + ………….
(v) 250 + 211 + …………. = 211 + 134 + 250
(vi) 433 + …………. = 123 + 433
(vii) 102 + …………. = 326 + 102
(viii) 361 + …………. = 361
(ix) …………. + 537 + 216 = 909 + 537 + 216
(x) …………. + 773 = 773 + 612
Answers:
6. (i) 3,07,689
(ii) 0
(iii) 11,301,000
(iv) 18,95,72,025
(v) 22,68,592
(vi) 37,66,442
(vii) 210,718,660
(i) 674
(ii) 174
(iii) 122
(iv) 118
(v) 134
(vi) 123
(vii) 326
(viii) 0
(ix) 909
(x) 612
7. Fill in the given blanks using the properties of addition:
(i) 9508 + 8857 = ……………. + 9508
(ii) 6698 + ……………. = 6698
(iii) 7397 + 1 = …………….
(iv) 8647 + ……………. = 8648
(v) 7498 + ……………. = 5096 + 7498
(vi) ……………. + 0 = 2985
(vii) (6654 + 3011) + 8010 = 6654 + (……………. + 8010)
(viii) 3997 + 2000 = …………….
(ix) ……………. Added to 50 = 150
(x) 1 more than 999 = …………….
Answers:
7. (i) 8857
(ii) 0
(iii) 7398
(iv) 1
(v) 5096
(vi) 2985
(vii) 3011
(viii) 5997
(ix) 100
(x) 1000
8. Write the successor of the following numbers:
(i) 433
(ii) 127
(iii) 484
(iv) 579
(v) 397
(vi) 625
(vii) 650
(viii) 823
(ix) 34
(x) 0
Answer:
8. (i) 434
(ii) 128
(iii) 485
(iv) 580
(v) 398
(vi) 626
(vii) 651
(viii) 824
(ix) 35
(x) 1
- The Number Zero
- Properties of Whole Numbers
- Successor and Predecessor
- Representation of Whole Numbers on Number Line
- Properties of Addition
- Properties of Subtraction
- Properties of Multiplication
- Properties of Division
- Division as The Inverse of Multiplication
From Properties of Addition to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
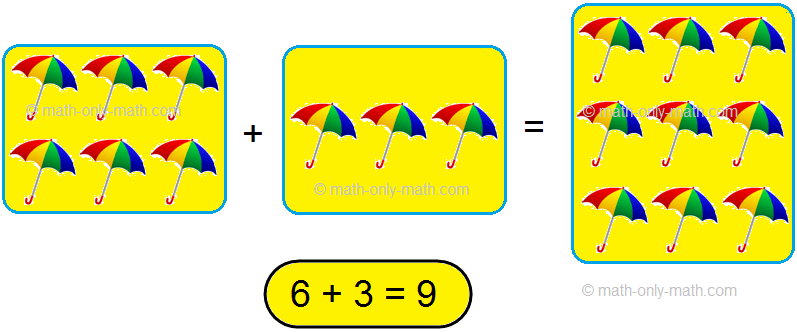
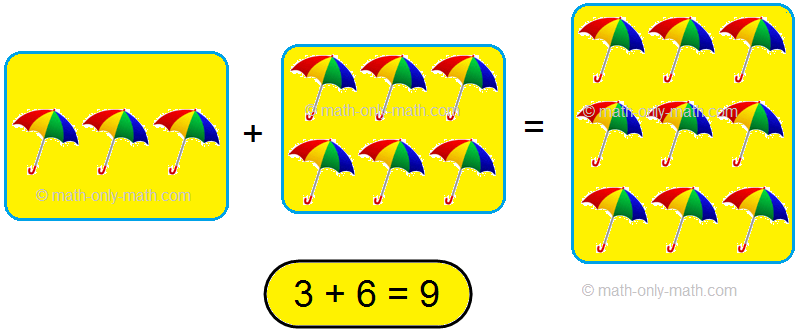




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.