Properties of Subtraction

Some properties of subtraction of whole numbers are:

Property I:

If a and b are two whole numbers such that a > b or a = b, then a – b is a whole number. If a < b, then subtraction a – b is not possible in whole numbers.

For example:

9 - 5 = 4

87 - 36 = 51

130 - 60 = 70

119 - 59 = 60

28 - 0 = 28

Property II:

The subtraction of whole numbers is not commutative, that is, if a and b are two whole numbers, then in general a – b is not equal to (b – a).

Verification:

We know that 9 – 5 = 4 but 5 – 9 is not possible. Also, 125 – 75 = 50 but 75 – 125 is not possible. Thus, for two whole numbers a and b if a > b, then a – b is a whole number but b – a is not possible and if b > a, then b – a is a whole number but a – b is not possible.

Hence, in general (a – b) is not equal to (b – a)

Property III:

If a is any whole number other than zero, then a – 0 = a but 0 – a is not defined.

Verification:

We know that 15 – 0 = 15, but 0 – 15 is not possible.

Similarly, 39 – 0 = 39, but 0 – 39 is not possible.

Again, 42 – 0 = 42, but 0 – 42 is not possible.

Property IV:

The subtraction of whole numbers is not associative. That is, if a, b, c are three whole numbers, then in general a – (b – c) is not equal to (a – b) – c.

Verification:

We have,

20 – (15 – 3) = 20 – 12 = 8,

and, (20 – 15) – 3 = 5 – 3 = 2

Therefore, 20 – (15 – 3) ≠ (20 – 15) – 3.

Similarly, 18 – (7 – 5) = 18 – 2 = 16,

and, (18 – 7) – 5 = 11 – 5 = 6.

Therefore, 18 – (7 – 5) ≠ (18 – 7) – 5.

Property V:

If a, b and c are whole numbers such that a – b = c, then b + c = a.

Verification:

We know that 25 – 8 = 17. Also, 8 + 17 = 25

Therefore, 25 – 8 = 17 or, 8 + 17 = 25

Similarly 89 – 74 = 15 because 74 + 15 = 89.

● Zero Property of Subtraction - When zero is subtracted from the number, the difference is the number itself.

For example,

(i) 8931 – 0 = 8931;

(ii) 5649 – 0 = 5649;

(iii) 245 – 0 = 245

(iv) 197 – 0 = 197

● Properties of Subtraction of a Number from itself: When a number is subtracted from itself the difference is zero.

For example,

(i) 5485 – 5485 = 0

(ii) 345 – 345 = 0

(iii) 279 – 279 = 0

● Predecessor – On subtracting 1 from any number, we get the number just before it. When 1 is subtracted from a number, we get its predecessor.

For example,

(i) 6001 – 1 = 6000

(ii) 6000 – 1 = 5999

(iii) 163 – 1 = 162

(iv) 171 – 1 = 170

Worksheet on Properties of Subtraction:

I. Fill in the blanks:

(i) 568 – 0 = …………….

(ii) 7530 – 4530 = …………….

(iii) 7790 – 1 = …………….

(iv) 65894 – 65893 = …………….

(v) 54172 - ……………. = 0

(vi) 8688 – 8288 = …………….

(vii) 7721 – 5620 = …………….

(viii) 17281 – 1 = …………….

(ix) ……………. – 1 = 29999

(x) 29080 - ……………. = 29079

(xi) 548 - ………….. = 0

(xii) ………….. – 0 = 274

(xiii) 367 - ………….. = 367

(xiv) 765 – 765 = …………..

(xv) 212 – 0 = …………..

(xvi) 167 - ………….. = 0

(xvii) 647 – 647 = …………..

(xviii) 326 – 326 = …………..

(xix) ………….. – 0 = 876

(xx) 429 – 0 = …………..

(xxi) 999 – 999 = …………..

(xxii) 412 - ………….. = 412

(xxiii) 700 - 100 = …………..

(xxiv) 100 - 10 = …………..

(xxv) 9429 - 100 = …………..

(xxvi) 4583 - 1000 = …………..

(xxvii) 9498 - 1000 = …………..

(xxviii) 1000 - 1000 = …………..

Answers:

(i) 568

(ii) 3000

(iii) 7789

(iv) 1

(v) 54172

(vi) 400

(vii) 2101

(viii) 17280

(ix) 30000

(x) 1

(xi) 54

(xii) 274

(xiii) 0

(xiv) 0

(xv) 212

(xvi) 167

(xvii) 0

(xviii) 0

(xix) 876

(xx) 429

(xxi) 0

(xxii) 0

(xxiii) 600

(xxiv) 90

(xxv) 9329

(xxvi) 3583

(xxvii) 8498

(xxviii) 0

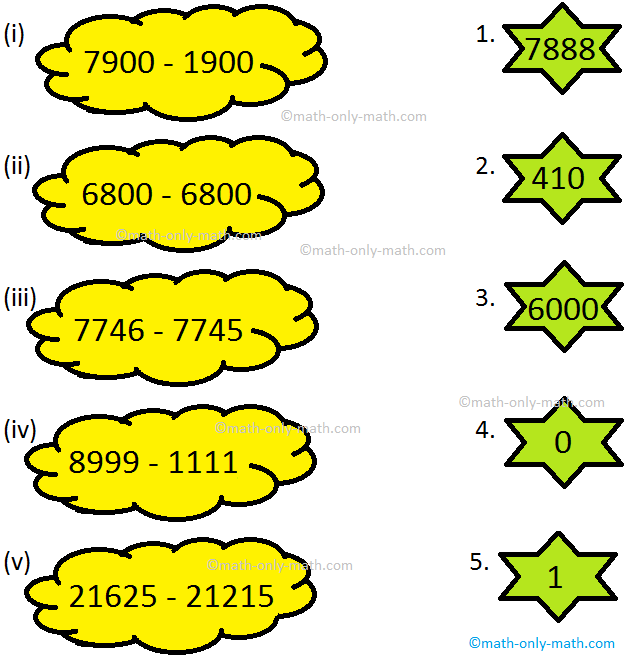
II. Match the given difference to its solution by coloring the cloud and the shape with same color.

Answer:

(i) → 3

(ii) → 4

(iii) → 5

(iv) → 1

(v) → 2

III. Write the predecessor of the following numbers:

(i) 259 …………..

(ii) 608 …………..

(iii) 450 …………..

(iv) 374 …………..

(v) 900 …………..

(vi) 529 …………..

(vii) 201 …………..

(viii) 598 …………..

Answers:

III. (i) 258

(ii) 607

(iii) 449

(iv) 373

(v) 899

(vi) 528

(vii) 200

(viii) 597

IV: Fill in the blanks on the basis of subtraction facts:

(i) 43 - 0 = _____

(ii) 18 - 1 = _____

(iii) 77 - 77 = _____

(iv) 54 - 0 = _____

(v) 33 - 1 = _____

(vi) 62 - 0 = _____

(vii) 98 - 1 = _____

(viii) 56 - 56 = _____

(ix) 34 - 0 = _____

Answer:

IV: (i) 43

(ii) 17

(iii) 0

(iv) 54

(v) 32

(vi) 62

(vii) 97

(viii) 0

(ix) 34

Math Only Math is based on the premise that children do not make a distinction between play and work and learn best when learning becomes play and play becomes learning.

However, suggestions for further improvement, from all quarters would be greatly appreciated.

Numbers Page 

6th Grade Page 

From Properties of Subtraction to HOME PAGE