Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Reading and Writing Large Numbers
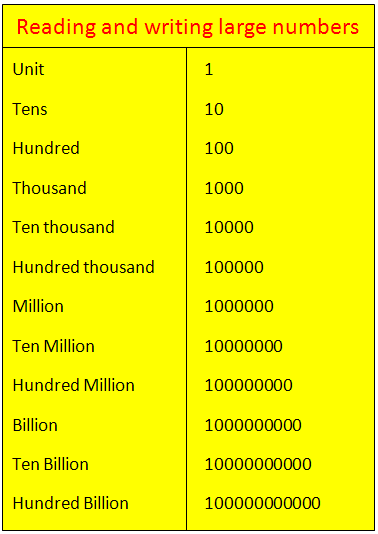
In reading and writing large numbers we group place values into periods ‘ones or unit’, ‘tens’, ‘hundred’, ‘thousand’, ‘10 thousand’, ‘100 thousand’, ‘million’, ’10 million’, ‘100 million’, ‘billion’, ’10 billion’, ‘100 billion’, ‘trillion’ are periods.
For example:
Ones/Unit = 1
Tens = 10
Hundred = 100
Thousand = 1,000
10 Thousand = 10,000
100 Thousand = 100,000
Million = 1,000,000
10 Million = 10,000,000
100 Million = 100,000,000
Billion = 1,000,000,000
10 Billion = 10,000,000,000
100 Billion = 100,000,000,000
The below diagram will help us to get the better concept on facts about reading and writing large numbers.
So, while reading or writing a large number we need to start from the left side with the largest group and move to the right side.
Reading and writing large numbers in words in thousand and hundred:
(i) 3,019 - Three thousand nineteen
(ii) 5,059 - Five thousand fifty-nine
(iii) 8,782 - Eight thousand seven hundred eighty-two
(iv) 41,018 - Forty-one thousand eighteen
(v) 52, 739 - Fifty– two thousand seven hundred thirty-nine
(vi) 621,011 - Six hundred twenty-one thousand eleven
(vii) 530,008 - Five hundred thirty thousand eight
(viii) 765,941 - Seven hundred sixty-five thousand nine hundred forty-one
Reading and writing large numbers in words in million, thousand and hundreds:
(i) 6,254,745 - Six million two hundred fifty-four thousand seven hundred forty-five
(ii) 31,286,271 - Thirty-one million two hundred eighty-six thousand two hundred seventy-one
(iii) 731,256,835 - Seven hundred thirty-one million two hundred fifty-six thousand eight hundred thirty-five
(iv) 651,356,851 - Six hundred fifty-one million three hundred fifty-six thousand eight hundred fifty-one
Reading and writing large numbers in words in billion, million, thousand and hundred:
(i) 4,451,638,534 - Four billion four hundred fifty-one million six hundred thirty-eight thousand five hundred thirty-four
(ii) 4,230,453,872 - Four billion two hundred thirty million four hundred fifty-three thousand eight hundred seventy-two
(iii) 51,462,648,572 - Fifty-one billion four hundred sixty-two million six hundred forty-eight thousand five hundred seventy-two
(iv) 42,230,453,896 - Forty-two billion two hundred thirty million four hundred fifty-three thousand eight hundred ninety-six
(v) 82,213,456,897 - Eighty-two billion two hundred thirteen million four hundred fifty-six thousand eight hundred ninety-seven
(vi) 641,496,632,823 - Six hundred forty-one billion four hundred ninety-six million six hundred thirty-two thousand eight hundred twenty-three
(vii) 981,482,637,874 - Nine hundred eighty-one billion four hundred eighty-two million six hundred thirty-seven thousand eight hundred seventy-four
(vii) 956,491,638,852 - Nine hundred fifty-six billion four hundred ninety-one million six hundred thirty-eight thousand eight hundred fifty-two.
Large Numbers
We have studied the following pattern regarding the smaller numbers:
Let us extend the same pattern to get the larger numbers:
We observe that the value of each place increases 10 times as we move one place from right to left, i.e., ones to tens, tens to hundreds, hundreds to thousands, etc.
However, to read numerals of larger numbers without difficulty, we group the places into periods in the place value chart.
These periods are usually separated by commas (,).
How to Read and Write Large Numbers in Lakhs and Crores:
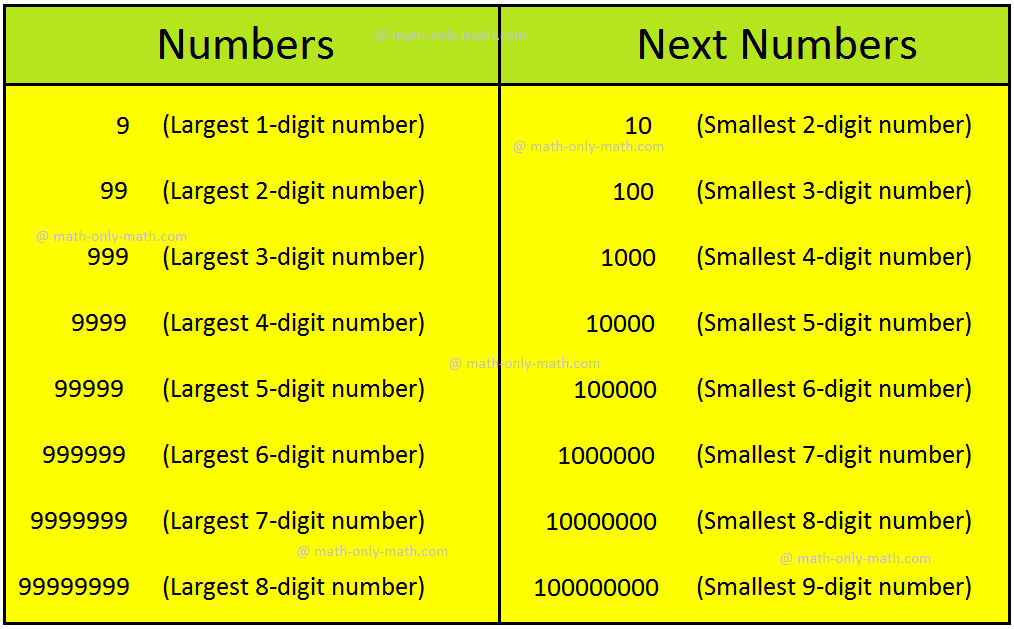
We know the largest 6-digit number is 999999.
Let us add 1 to it.
On adding 1 to 999999, we get the smallest 7-digit number 1000000.
This number is read as Ten Lakh.
To write 7-digit numbers, we add the next place value just to the left of lakhs as TL (Ten Lakhs).
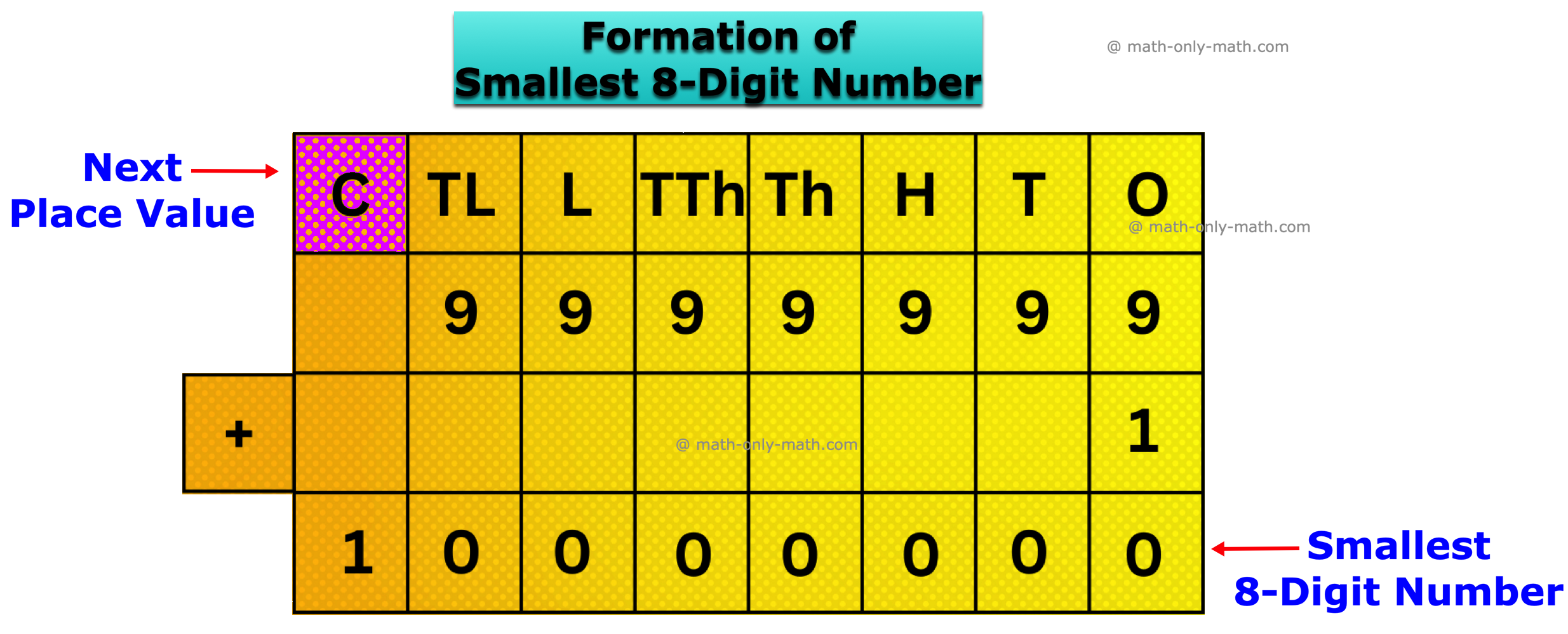
Similarly, the greatest 7-digit number is 9999999.
On adding 1 to it, we get the smallest 8-digit number 10000000.
This number is read as One crore.
To write 8-digit numbers, we add the next place value just to the left of Ten Lakhs as C (Crores).
As the numbers get larger and place values increase, we group the place values into periods.
This helps to read and write large numbers easily.
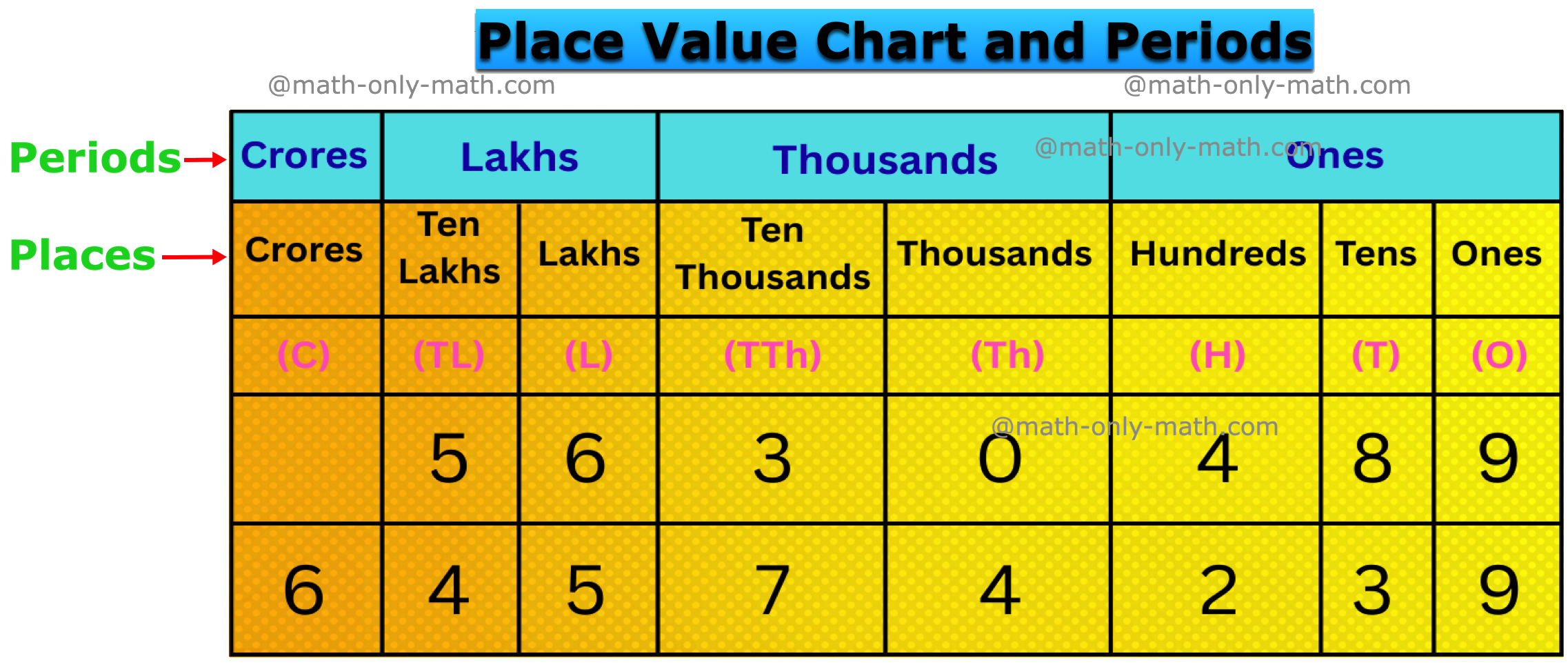
Place Value Chart and Periods of Large Numbers:
Let us now write the numbers given in this table in words.
5630489 - Fifty-six lakh thirty thousand four hundred eighty-nine.
64574239 - Six crore forty-five lakh seventy-four thousand two hundred thirty-nine.
Use Of Commas
To make reading and writing of 7 and 8-digit numbers easily, we insert commas between digits of each period.
For example:
5630489 → 56,30,489
64574239 → 6,45,74,239
Frequently asked questions on Reading and Writing Large Numbers:
1. The total number of 6-digit number is
(a) 9,000
(b) 90,000
(c) 9,00,000
(d) 900
1. The total number of 6-digit number is
(a) 9,000
(b) 90,000
(c) 9,00,000
(d) 900
Answer:
Greatest six-digit number = 9,99,999
Greatest five-digit number = 99,999
Total number of six-digit numbers 9,99,999 - 99,999 = 9,00,000
So, the option (c) is correct, which is the required answer, i.e., answer (c).
2. The total no. of 8-digit numbers is
(a) 9999999
(b) 90000000
(c) 10000000
(d) 99999999
2. The total no. of 8-digit numbers is
(a) 9999999
(b) 90000000
(c) 10000000
(d) 99999999
Answer:
Greatest eight-digit number = 9,99,99,999
Greatest seven-digit number = 99,99,999
Total number of eight-digit numbers 9,99,99,999 - 99,99,999
= 9,00,00,000
So, the option (b) is correct, which is the required answer, i.e., answer (b).
3. How many 5-digit numbers are there in all?
3. How many 5-digit numbers are there in all?
Answer:
Greatest five-digit number = 99,999
Greatest four-digit number = 9,999
Total number of five-digit numbers = 99,999 - 9,999
= 90,000
● Reading and Writing Large Numbers - Worksheets
Worksheet on Reading and Writing Large Numbers
From Reading and Writing Large Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.