Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Basic Trigonometric Ratios
To know about the basic trigonometric ratios with respect to a right-angled triangle,
|
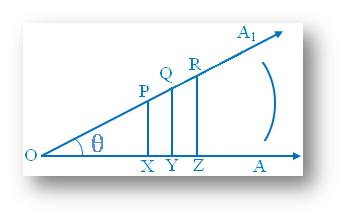
let a ray OA revolve in the anti-clockwise direction and assume the position OA1, so that an angle ∠AOA1 = θ is formed. Now any number of points P, Q, R, .......... are taken on OA1, and perpendiculars PX, QY, RZ, ........ are drawn on OA from those points respectively. |
All the right-angled triangles POX, QOY, ROZ, ......... are similar to each other.
Now from the properties of similar triangles we know,|
(i) PX/OP = QY/OQ = RZ/OR = ..... (iii) PX/OX = QY/ OQ = RZ/OZ = ..... (v) OP/OX = OQ/OX = OR/OZ = ..... |
(ii) OX/OP = QY/OQ = OZ/OR = ..... (iv) OP/PX = OQ/QY = OR/RZ = ..... (vi) OX/PX = OY/QY = OZ/RZ = ..... |
Thus we see in a set of similar right-angled triangles with respect to the same acute angle
(i) perpendicular : hypotenuse i.e., perpendicular/hypotenuse remains same.
(ii) base : hypotenuse and
(iii) perpendicular : base do not change for the aforesaid similar right-angled triangles. So we can say that the values of these ratios do not depend on the size of triangles or the length of their sides. The values entirely depend on the magnitude of the acute angle θ.
It is so because all the triangles are right angled triangles having a common acute angle θ. Similar relations will hold whatever be the measure of the acute angle θ.
So we see that in similar right-angled triangles the ratio of any two sides, with reference to a common acute angle, give a definite value. This is the concept on the basis trigonometric ratios.
Again we have shown that the ratio of any two sides of a right-angled triangle, have six different ratios.
These six ratios are identified by six different names, one for each.
Now we will define trigonometrical ratios of positive acute angles and their relations.
Definitions of Trigonometrical Ratios:
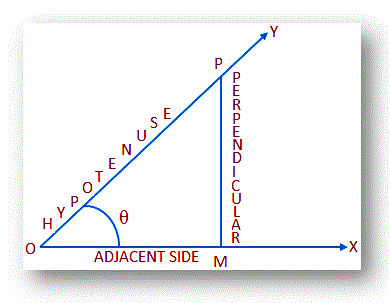
Now, the six trigonometrical ratios of the angle θ are defined as follows:
What are the six trigonometrical ratios?
Perpendicular/Hypotenuse = PM/OP = sine of the angle θ;or, sin θ = PM/OP
Adjacent/Hypotenuse = OM/OP = cosine of the angle θ;
or, cos θ = OM/OP
Perpendicular/Adjacent = PM/OM = tangent of the angle θ;
or, tan θ = PM/OM
Hypotenuse/Perpendicular = OP/PM = cosecant of the angle θ;
or, csc θ = OP/PM
Hypotenuse/Adjacent = OP/OM= secant of the angle θ;
or, sec θ = OP/OM
and Adjacent/Perpendicular = OM/PM = cotangent of the angle θ;
or, cot θ = OM/PM
The six ratios sin θ, cos θ, tan θ, csc θ, sec θ and cot θ are called Trigonometrical Ratios of the angle θ.
Sometimes there are two other ratios in addition. They are known as Versed sine and Coversed sine.
These two ratios are defined as follows:
Versed sine of angle θ or Vers θ = 1 - cos θ
and Coversed sine of angle θ or Coverse θ = 1 - sin θ.
Note:
(i) Since each trigonometrical ratio is defined as the ratio of two lengths hence each of them is a pure number.
(ii) Note that sin θ does not imply sin × θ; in fact, it
represents the ratio of perpendicular and hypotenuse with respect to the angle θ of a right-angled triangle.
(iii) In a right-angled triangle the side opposite to right-angle is the
hypotenuse, the side opposite to given angle θ is the perpendicular and the
remaining side is the adjacent side.
Relations Between the Trigonometric Ratios
Problems on Trigonometric Ratios
Reciprocal Relations of Trigonometric Ratios
Problems on Trigonometric Identities
Elimination of Trigonometric Ratios
Eliminate Theta between the equations
Verify Trigonometric Identities
From Basic Trigonometric Ratios to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 22, 25 03:02 PM
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:58 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
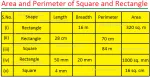
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.