Subscribe to our YouTube channel for the latest videos, updates, and tips.
Subtraction of Length
The process of subtraction of units of length is exactly similar to that of subtraction of ordinary numbers.
Learn how the values of length are arranged in different columns for the subtraction of length.
1. Subtract 12 m 36 cm from 48 m 57 cm
Solution:
Case 1:
Minuend and subtrahend are both converted into smaller units.
12 m 36 cm = (12 × 100) cm + 36 cm = (1200 + 36) cm = 1236 cm
48 m 57 cm = (48 × 100) cm + 57 cm = (4800 + 57) cm = 4857 cm
Now subtract
48 m 57 cm = 4857 cm
- 12 m 36 cm = - 1236 cm
3621 cm
= 3600 cm + 21 cm
= 36 m 21 cm
Therefore, 48 m 57 cm - 12 m 36 cm = 36 m 21 cm
Case 2:
As minuend is greater than subtrahend, the minuend is placed above the subtrahend. Then m and cm are arranged in different columns.
Now subtract
m cm
48 57
- 12 36
36 21
(i) Subtracting cm, 57 cm - 36 cm = 21 cm.
It is placed under cm column.
(ii) Subtracting m, 48 m - 12 m = 36 m.
It is placed under m column.
Hence, difference = 36 m 21 cm
2. Subtract 37 m 50 cm from 53 m 30 cm.
Solution:
Case 1:
Minuend and subtrahend are both converted into smaller units.
53 m 30 cm = (53 × 100) cm + 33 cm = (5300 + 30) cm = 5330 cm
37 m 50 cm = (37 × 100) cm + 50 cm = (3700 + 50) cm = 3750 cm
Now subtract
5330 cm
- 3750 cm
1580 cm
= 1500 cm + 80 cm
= 15 m 80 cm
Therefore, 53 m 30 cm - 37 m 50 cm = 15 m 80 cm.
Case 2:
As minuend is greater than subtrahend, the minuend is placed above the subtrahend. Then m and cm are arranged in different columns. Minuend 53 m 30 cm is placed above subtrahend 37 m 50 cm.
m cm
1 100
53 30
- 37 50
15 80
(i) 50 cm > 30 cm. So, 50 cm cannot be subtracted from 30 cm.
1 m or 100 cm is borrowed from 53 m leaving 52 m making 30 cm to 130 cm.
Now 130 - 50 = 80. It is placed under cm column.
(ii) Now in the m column, 53 - 1 = 52 m. 52 m - 37 m = 15 m.
It is placed under m column.
Hence, the difference is 15 m 80 cm.
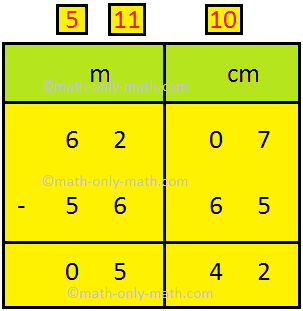
3. Subtract 56 m 65 cm from 62 m 7 cm.
|
Solution: Let us subtract. Step I: Arrange the numbers vertically. Step II: Write the lengths to be subtracted in m and cm as shown. Step III: First, subtract centimetres from right and then subtract the metres. |
Thus, 62 m 7 cm - 56 m 65 cm = 5 m 42 cm
4. Subtract 37 m 6 cm from 70 m.
Solution:
Case 1:
We have, 70 m - 37 m 6 cm
Minuend and subtrahend are both converted into smaller units.
70 m = (70 × 100) cm = 7000 cm
37 m 6 cm = (37 × 100) cm + 6 cm = (3700 + 6) cm = 3706 cm
Now subtract
7000 cm
- 3706 cm
3294 cm
= 3200 cm + 94 cm
= 32 m 94 cm
Therefore, 70 m - 37 m 6 cm = 32 m 94 cm.
Case 2:
As minuend is greater than subtrahend, the minuend is placed above the subtrahend. Then m and cm are arranged in different columns. Minuend 70 m 00 cm is placed above subtrahend 37 m 06 cm.
m cm
1 100
70 00
- 37 06
32 94
(i) 06 cm > 0 cm. So, 6 cm cannot be subtracted from 0 cm.
1 m or 100 cm is borrowed from 70 m leaving 69 m in m column.
(ii) Now 100 cm - 06 cm = 94 cm. It is placed under cm column.
(iii) Now in the m column, 69 m - 37 m = 32 m.
It is placed under m column.
Hence, the difference is 32 m 94 cm.
5. Subtract 45 km 282 m from 63 km 70 m.
Solution:
Case 1:
Minuend and subtrahend are both converted into smaller units (conversion method).
63 km 70 m = (63 × 1000) m + 70 m = (63000 + 70) m = 63070 m
45 km 282 m = (45 × 1000) m + 282 m = (45000 + 282) m = 45282 m
Now subtract
63070 m
- 45282 m
17788 m
= 17000 m + 788 m
= 17 km 788 m
Therefore, 63 km 70 m - 45 km 282 m = 17 km 788 m.
Case 2:
As
minuend is greater than subtrahend, the minuend is placed above the
subtrahend. Then km and m are arranged in different columns. Minuend 63 km 70 m is placed above subtrahend 45 km 282 m (without conversion).
km m
1 1000
63 070
- 45 282
17 788
(i) 282 m > 70 m. So, 282 m cannot be subtracted from 70 m.
1 km or 1000 m is borrowed from 63 km leaving 62 km making 70 m to 1070 m (Since, 1 km = 1000 m and 70 m = 1070 m).
Now 1070 m - 282 m = 788 m. It is placed under m column.
(ii) Now in the km column, 63 - 1 = 62 km. 62 km - 45 km = 17 km.
It is placed under km column.
Hence, the difference is 17 km 788 m.
6. Subtract 75 km 345 m from 200 km 20 m.
Solution:
As minuend is greater than subtrahend, the minuend is placed above the subtrahend. Then km and m are arranged in different columns. Minuend 200 km 20 m is placed above subtrahend 75 km 345 m.
km m
1 1000
200 020
- 275 345
124 675
(i) 345 m > 20 m. So, 345 m cannot be subtracted from 20 m.
1 km or 1000 m is borrowed from 200 km leaving 199 km making 020 m to 1020 m.
Now 1020 m - 345 m = 675 m. It is placed under m column.
(ii) Now in the km column, 200 - 1 = 199 km. 199 km - 75 km = 124 km.
It is placed under km column.
Hence, the difference is 124 km 675 m.
7. Subtract 8 m 7 dm 5 cm from 26 m 4 dm 8 cm.
Solution:
As minuend is greater than subtrahend, the minuend is placed above the subtrahend. Then m, dm and cm are arranged in different columns. Minuend 26 m 4 dm 8 cm is placed above subtrahend 8 m 7 dm 5 cm.
m dm cm
1 10
26 4 8
- 8 7 5
17 7 3
(i) 8 cm - 5 cm = 3 cm. It is placed under cm column.
(ii) 7 dm > 4 dm. So, 7 dm cannot be subtracted from 4 dm.
1 m or 10 dm is borrowed from 26 m leaving 25 m making 4 dm to 14 dm.
Now 14 dm - 7 dm = 7 dm. It is placed under dm column.
(iii) Now in the m column, 26 - 1 = 25 m. 25 m - 8 m = 17 m.
It is placed under m column.
Hence, the difference is 17 m 7 dm 3 cm.
To subtract lengths, write the numbers of km, m and cm in separate columns then subtract like ordinary numbers, starting from right.
8. Subtract 11 m 35 cm from 24 m 45 cm.
Solution:
m cm
24 45
- 11 35
__ 13 10
Answer: 13 m 10 cm
9. Subtract 29 m 84 cm from 69 m 66 m.
Solution:
m cm
18
5 8 16
6 9 6 6
- 2 9 8 4
__ 3 7 8 2
Answer: 37 m 82 cm
10. Subtract following lengths:
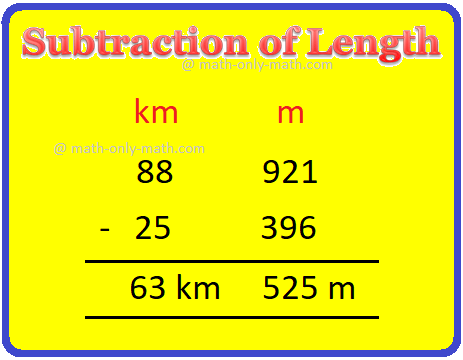
(i) 25 km 396 m from 88 km 921 m
(ii) 7 m 24 cm from 77 m 94 cm
Solution:
|
(i) 25 km 396 m from 88 km 921 m 88 km 921 m - 25 km 396 m First subtract m = (921 - 396) m = 525 m Now subtract km = (88 - 25) km = 63 km |
Therefore, the required difference is 63 km 525 m
|
(ii) 7 m 24 cm from 77 m 94 cm 77 m 94 cm - 7 m 24 cm First subtract cm = 94 cm - 24 cm = 70 cm Now subtract m = 77 m - 7 m = 70 m |
Therefore, the required difference is 70 cm 70 m
Word Problems on Subtraction of Length:
SUBTRACTION OF METRES AND CENTIMETRES
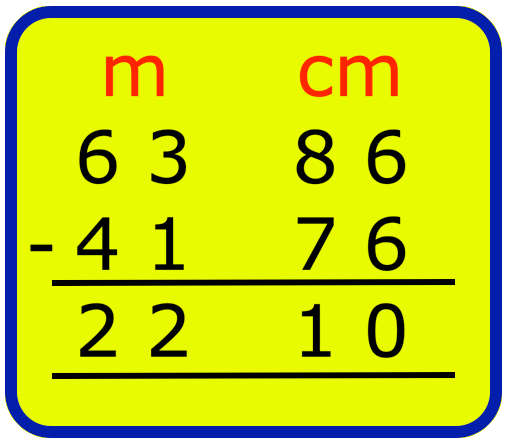
1. Michael, the cloth merchant, had 63 metres 86 centimetres of green cloth. He sold 41 metres 76 centimetres of it. How much cloth is left with him now?
Solution:
Write m and cm in columns as shown.
|
Step I: Subtract cm first. 86 - 76 = 10 Write 10 in the cm column. Step II: Subtract m now. 63 - 41 = 22 Write 22 in the m column. |
Therefore, the length of the green cloth left is 22 m 10 cm.
Worksheet on Subtraction of Length:
1. Subtract the following:
(i) 81 m 9 cm - 52 m 52 cm
(ii) 28 m 98 cm - 16 m 20 cm
(iii) 352 m 917 cm - 148 m 79 cm
(iv) 938 m 33 cm - 619 m 57 cm
(v) 394 m 68 cm - 45 m 79 cm
(vi) 180 m 90 cm - 42 m 33 cm
Answer:
1. (i) 28 m 57 cm
(ii) 12 m 78 cm
(iii) 203 m 38 cm
(iv) 318 m 76 cm
(v) 348 m 89 cm
(vi) 138 m 57 cm
2. Subtract the following:
(i) 81 m 09 cm from 145 m 56 cm
(ii) 14 m 82 cm from 67 m 40 cm
(iii) 174 m 259 cm from 512 m 36 cm
(iv) 79 m 56 cm from 140 m 23 cm
(v) 180 m 90 cm from 287 m 46 cm
Answer:
2. (i) 64 m 47 cm
(ii) 52 m 58 cm
(iii) 338 m 11 cm
(iv) 60 m 67 cm
(v) 106 m 56 cm
3. Subtract the following lengths:
|
(i) |
m cm 63 87 - 32 50 _____________ |
(ii) |
m cm 39 75 - 16 05 _____________ |
|
(iii) |
m cm 28 54 - 12 30 _____________ |
(iv) |
m cm 43 65 - 21 40 _____________ |
|
(v) |
m cm 90 85 - 40 30 _____________ |
(vi) |
m cm 18 72 - 14 20 _____________ |
|
(vii) |
m cm 11 55 - 03 24 _____________ |
(viii) |
m cm 12 75 - 11 35 _____________ |
|
(ix) |
m cm 50 34 - 37 58 _____________ |
(x) |
m cm 64 20 - 35 65 _____________ |
|
(xi) |
m cm 73 38 - 57 19 _____________ |
(xii) |
m cm 81 56 - 43 15 _____________ |
|
(xiii) |
m cm 40 72 - 19 45 _____________ |
(xiv) |
m cm 80 72 - 69 85 _____________ |
|
(xv) |
m cm 40 38 - 16 59 _____________ |
(xvi) |
m cm 33 80 - 09 69 _____________ |
Answer:
3. (i) 31 m 37 cm
(ii) 23 m 70 cm
(iii) 16 m 24 cm
(iv) 22 m 25 cm
(v) 50 m 55 cm
(vi) 4 m 52 cm
(vii) 8 m 31 cm
(viii) 1 m 40 cm
(ix) 12 m 76 cm
(x) 28 m 55 cm
(xi) 16 m 19 cm
(xii) 38 m 41 cm
(xiii) 21 m 27 cm
(xiv) 10 m 87 cm
(xv) 23 m 79 cm
(xvi) 24 m 11 cm
You might like these
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Time duration tells us how long it takes for an activity to complete. We will learn how to calculate the time duration in minutes and in hours. Time Duration (in minutes) Ron and Clara play badminton every evening. Yesterday, their game started at 5 : 15 p.m.
Telling Time in 5-minute Intervals | Read the Clock |Nearest 5 Minutes
The clock has numbers from 1 to 12 marked on its dial. These numbers divide the clock face into 12 equal parts. Between any two numbers there are 5 small divisions. Each small division represents a minute. So, the minute hand takes 5 minutes more from one number to the next
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is the last month of the year. A year has 365 days.
Measurement of Time | Time | Clock | Hours | Minutes | Seconds
We know that the measurement of time is read by a clock or a watch. Any clock or watch except a digital watch, has a dial. On the circular border of the dial of a watch or clock there are the
Worksheet on Interpreting a Calendar | Questions on Calendar
In worksheet on interpreting a calendar, all grade students can practice the questions on calendar. This exercise sheet on interpreting a calendar can be practiced by the students to get more ideas to find the leap year. 1. How many months are there having (i) 31 days
Conversion of Hours into Minutes | Hours to Minutes Conversion | Time
We will discuss here about the conversion of hours into minutes. We know 1 hour is equal to 60 minutes which is required to convert the measuring time from hours to minutes.
Reading and Interpreting a Calendar | Calendar | Reading a Calendar
In reading and interpreting a calendar we need to know days in a week, days in a month and months in a year. There are 7 days in a week. The first day of the week is Sunday.
Use of Antemeridian and Postmeridian |Antemeridian am| Postmeridian pm
We will learn about the use of antemeridian and postmeridian. In English system the day starts at midnight and ends at the next midnight. The day begins just after 12 o’clock at midnight.
Telling the Time | Teaching Time | Analogue Clock| Reading Time
Teaching time is an interactive activity for telling time. This activity helps students to learn how to read the clock to tell time using the analogue clock. While reading or observing the time on a
Worksheet on Measurement | Problems on Measurement | Homework |Answers
In worksheet on measurement we will solve different types of questions on measurement of length, conversion of length, addition and subtraction of length, word problems on addition of length, word problems subtraction of length, measurement of weight
Worksheet on Subtraction of Capacity | Word Problems on Capacity | Ans
Practice the third grade math worksheet on subtraction of capacity. This sheet provides different types of questions where you need to arrange the values of capacity under
Worksheet on Addition of Capacity | Word Problems on Adding capacity
Practice the third grade math worksheet on addition of capacity. This sheet provides different types of questions where you need to arrange the values of capacity under different columns of litres and
Subtraction of Capacity | Units of Capacity and Volume | Examples
In subtraction of capacity we will learn how to find the difference between the units of capacity and volume. While subtracting we need to follow that the units of capacity
Addition of Capacity | Add the Different Units of Capacity | Examples
In addition of capacity we will learn how to add the different units of capacity and volume together. While adding we need to follow that the units of capacity i.e., liter and milliliter
Units of Capacity and Volume Conversion Chart | Metric Conversion
Units of capacity and volume conversion chart are discussed here in metric conversion of capacity and volume and also in customary units of capacity and volume. In math when we use capacity and volume, we normally use liter to represent as the standard unit, and the other
● Related Concepts
● Conversion of Standard Unit of Length
From Subtraction of Length to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
May 07, 25 01:48 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
May 07, 25 01:33 AM
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima… -
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
May 06, 25 01:23 AM
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by… -
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
May 06, 25 12:01 AM
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps -
Word Problems on Decimals | Decimal Word Problems | Decimal Home Work
May 05, 25 01:27 AM
Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.