Proof of Compound Angle Formula
sin (α - β)

We will learn step-by-step the proof of compound angle formula sin (α - β). Here we will derive formula for trigonometric function of the difference of two real numbers or angles and their related result. The basic results are called trigonometric identities.

The expansion of sin (α - β) is generally called subtraction formulae. In the geometrical proof of the subtraction formulae we are assuming that α, β are positive acute angles and α > β. But these formulae are true for any positive or negative values of α and β.

Now we will prove that, sin (α - β) = sin α cos β - cos α sin β; where α and β are positive acute angles and α > β.

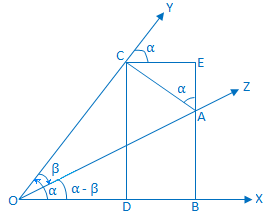
Let a rotating line OX rotate about O in the anti-clockwise direction. From starting position to its initial position OX makes out an acute ∠XOY = α.

Now, the rotating line rotates further in the clockwise direction and starting from the position OY makes out an acute ∠YOZ = β (which is < α).

Thus, ∠XOZ = α - β.    

We are suppose to prove that, sin (α - β) = sin α cos β - cos α sin β.

Construction: On the bounding line of the compound angle (α - β) take a point A on OZ and draw AB and AC perpendiculars to OX and OY respectively. Again, from C draw perpendiculars CD and CE upon OX and produced BA respectively.

Proof: From triangle ACE we get, ∠EAC = 90° - ∠ACE = ∠YCE = corresponding ∠XOY = α.

Now, from the right-angled triangle AOB we get,

sin (α - β) = $\frac{BA}{OA}$

               = $\frac{BE - EA}{OA}$

               = $\frac{BE}{OA}$ - $\frac{EA}{OA}$

               = $\frac{CD}{OA}$ - $\frac{EA}{OA}$

               = $\frac{CD}{OC}$ ∙ $\frac{OC}{OA}$ - $\frac{EA}{AC}$ ∙ $\frac{AC}{OA}$

               = sin α cos β - cos ∠CAE sin β  

               = sin α cos β - cos α sin β, (since we know, ∠CAE = α)

Therefore, sin (α - β) = sin α cos β - cos α sin β. Proved

1. Using the t-ratios of 30° and 45°, find the values of sin 15°.              

Solution:    

   sin 15°

= sin (45° - 30°)

= sin 45° cos 30° - cos 45° sin 30°

= ($\frac{1}{√2}$ ∙ $\frac{√3}{2}$) - ($\frac{1}{√2}$ ∙ $\frac{1}{2}$)

= $\frac{√3 - 1}{2√2}$

2. Prove that sin (40° + A) cos (10° + A) - cos (40° + A) sin (10° + A) = 1/2.

Solution:

L.H.S. = sin (40° + A) cos (10° + A) - cos (40° + A) sin (10° + A)

= sin {(40° + A) - (10° + A)}, [Applying the formula of sin α cos β - cos α sin β = sin (α - β)]

= sin (40° + A - 10° - A)

= sin 30°

= ½.

3. Simplify: $\frac{sin (x  -  y)}{sin x sin y}$ + $\frac{sin (y  -  z)}{sin y sin z}$ + $\frac{sin (z  -  x)}{sin z sin x}$

Solution:

 First term of the given expression = $\frac{sin (x   -   y)}{sin x sin y}$

= $\frac{sin x cos y  -  cos x sin y}{sin x sin y}$

= $\frac{sin x cos y}{sin x sin y}$ - $\frac{cos x sin y}{sin x sin y}$

= cot y - cot x.

Similarly, second term = $\frac{sin (y  -  z)}{sin y sin z}$ = cot z - cot y.

And third term = $\frac{sin (z  -  x)}{sin z sin x}$ = cot x - cot z.

Therefore,

$\frac{sin (x  -  y)}{sin x sin y}$ + $\frac{sin (y  -  z)}{sin y sin z}$ + $\frac{sin (z  -  x)}{sin z sin x}$

= cot y - cot x + cot z - cot y + cot x - cot z

= 0.

● Compound Angle

• Proof of Compound Angle Formula sin (α + β)
• Proof of Compound Angle Formula sin (α - β)
• Proof of Compound Angle Formula cos (α + β)
• Proof of Compound Angle Formula cos (α - β)
• Proof of Compound Angle Formula sin 22 α - sin 22 β
• Proof of Compound Angle Formula cos 22 α - sin 22 β
• Proof of Tangent Formula tan (α + β)
• Proof of Tangent Formula tan (α - β)
• Proof of Cotangent Formula cot (α + β)
• Proof of Cotangent Formula cot (α - β)
• Expansion of sin (A + B + C)
• Expansion of sin (A - B + C)
• Expansion of cos (A + B + C)
• Expansion of tan (A + B + C)
• Compound Angle Formulae
• Problems using Compound Angle Formulae
• Problems on Compound Angles

11 and 12 Grade Math

From Proof of Compound Angle Formula sin (α - β) to HOME PAGE