Multiplication using Number Lines

The number line can be used for multiplication.

Let us multiply 1-digit number using a number line.

For multiplying on the number line, we do skip counting.

For example, if we start from 0 and skip count in 2s, we will get 2, 4, 6, 8, 10 and so on, as shown on the number line below.

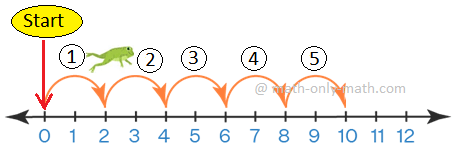
Now, let us multiply 6 by 3 on the number line.

Multiplying 6 by 3 means '6 times 3'. So we need to skip count six times in 3s.

So, we see that 6 x 3 = 18.

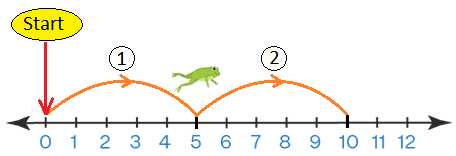
1. (a) Let us multiply 2 by 5 using a number line.

Take 5 jumps of 2 steps each. Where do we reach?

Start from 0. Take 5 jumps of 2 steps each. We reach 10.

2 + 2 + 2 + 2 + 2 = 10

or, 5 × 2 = 10

Now, take 2 jumps of 5 steps each. Where do we reach?

Start from 0. Take 2 jumps of 5 steps each. We again reach 10.

5 + 5 = 10

or, 2 × 5 = 10

The answer in multiplication is called the product.

So, 10 is the product of 2 and 5.

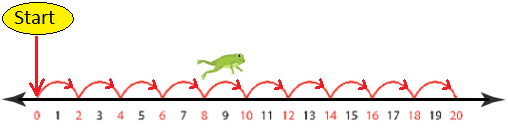
(b) Let us now multiply 2 and 10 on a number line.

Start from 0. Take 10 jumps of 2 steps each. You reach 20.

2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 20

or, 10 × 2 = 20

Start from 0. Take 2 jumps of 10 steps each. You again reach 20.

10 + 10 = 20

or, 2 × 10 = 20

10 × 2 = 20 and 2 × 10 = 20

or, 10 × 2 = 2 × 10 = 20

So, 20 is the product of 2 and 10.

2. Flippy wants to reach the pond. He jumps 3 steps each time.

4 jumps of 3 equal to 12

So, 4 × 3 = 12

3. Let us multiply 2 by 6.

Start from 0 and mark 6 groups of 2's to the right of 0. Then make 6 moves of 2 each as shown above. We reach at 12.

So, 2 × 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12

Note: Changing the order of numbers being multiplied does not change the product. This means that the product remains the same even if the order of the numbers is changed.

More Example:

(i) If 2 × 10 = 20, then 10 × 2 = 20

(ii) If 5 × 2 = 10, then 2 × 5 = 10

(iii) If 2 × 4 = 8, then 4 × 2 = 8

(iv) If 3 × 10 = 30, then 10 × 3 = 30

(v) If 5 × 3 = 15, then 3 × 5 = 15

(vi) If 3 × 4 = 12, then 4 × 3 = 12

Multiplication of Whole Numbers on Number Line

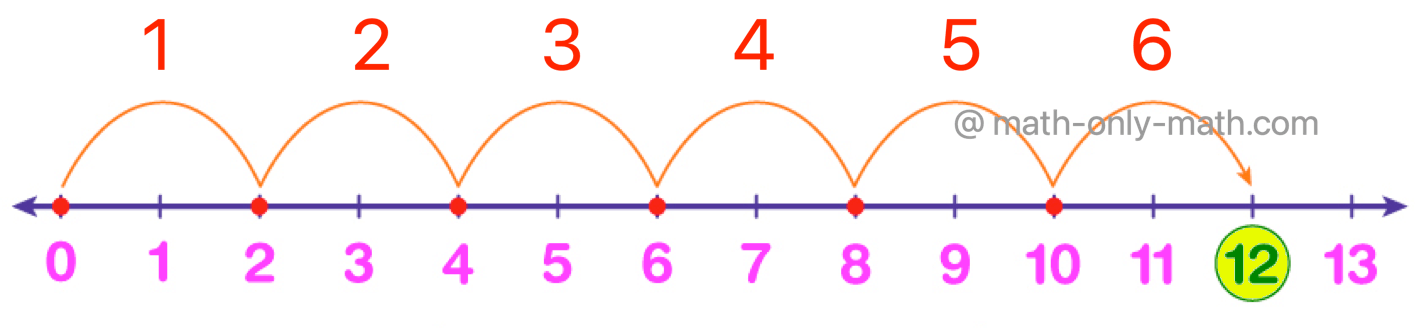
4. Using the number line, write the whole number which is a product of 2 and 3. Since multiplication is repeated addition, therefore, to evaluate 2 × 3, first start from 0, move 2 units at a time to the right making 3 such moves to obtain 6, as shown in the following figure.

Hence, 2 × 3 = 6.

1. Multiplication using Number Lines.

(i)

2 × 4 = __________

(ii)

4 × 2 = __________

2. Multiply on the number line. One has been done for you.

(i) 

4 × 5 = 20

(ii)

3 × 2 = _____

(iii)

7 × 1 = _____

(iv)

5 × 3 = _____

2nd Grade Math Practice

From Multiplication using Number Lines to HOME PAGE