Place Value and Face Value
FACE VALUE AND PLACE VALUE OF A DIGIT IN A NUMERAL
Face Value: The face value of a digit in a numeral is the actual value of a digit at whatever place it may be.
Place Value: The place value of a digit in a numeral depends on the position it occupies in a numeral.
Let us consider the numeral 675:
Arrange the digits of 675 in the place value chart as shown below:
H
T
O
6
7
5
From the place value chart, we have:
The place value of 6 = 6 hundreds
= 600; the face value of 6 = 6,
The place value of 7 = 7 tens
= 70; the face value of 7 = 7,
The place value of 5 = 5 ones
= 5; the face value of 5 = 5.
Note:
The place value of 0 is always zero, irrespective of its place in the numeral. For example, the place value of 0 in 609 and 805 is 0 in each case.
Let us look at the digits 1 and 2.
|
The digit 1 represents one object |
 |
|
The digit 2 represents two objects |
 |
We know that digit 2 is greater than the digit 1 or 2 > 1.
With the digits 1 and 2 we can make the numbers 12 and 21.
Face value is the value of a digit in a number.
So, the digit 1 has the same face value in both the numbers `12 and 21.
Similarly, the digit 2 has the same face value in the numbers 12 and 21.
Therefore, the face value of a digit always remains the same.
Face Value of a Number Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
We write 12 and 21 by using ones and tens as:
In the number 12, the value of 2 (i.e., 2 ones) is less than the value of 1 (i.e., 1 ten)
In the number 21, the value of 2 (i.e., 2 tens) is greater than the value of 1 (i.e., 1 one)
In both the numbers 12 and 21 there value is different this is because of its place value.
Place value of a digit is the value of a digit because of its place in a number.
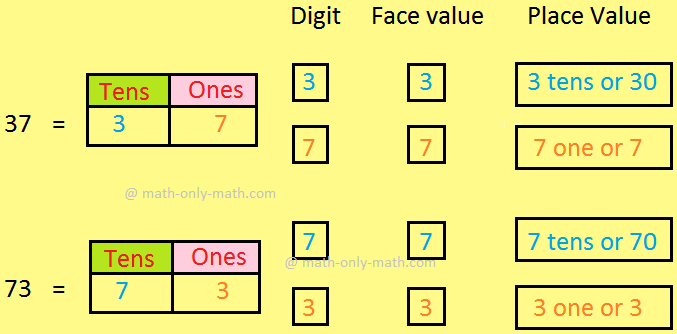
Similarly, the digit 3 and 7 can be used to make the number 37 and 73.
Place Value of a Number Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
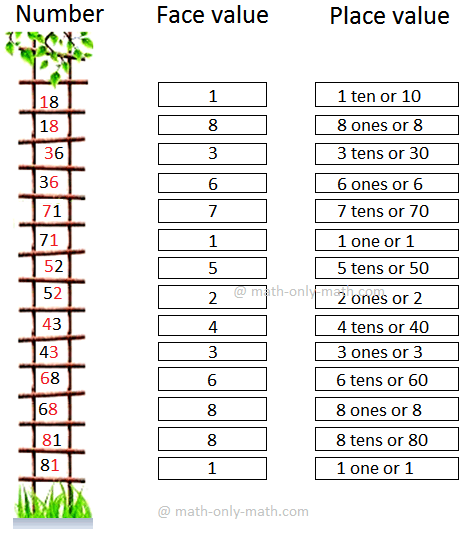
Let us look at the example to understand the difference of face value and place value.
Face value and place value of the digits are coloured in red.
|
Number 18 18 36 36 71 71 52 52 43 43 68 68 81 81 |
Face value Place value 1 1 ten or 10 8 8 ones or 8 3 3 tens or 30 6 6 ones or 6 7 7 tens or 70 1 1 one or 1 5 5 tens or 50 2 2 ones or 2 4 4 tens or 40 3 3 ones or 3 6 6 tens or 60 8 8 ones or 8 8 8 tens or 80 1 1 one or 1 |
Learn the easiest way to understand the basic concept on place value and face value in the second grade.
Suppose we write a number in figures 435 in words we write four hundred thirty five.
Thus,
435 means 4 hundreds 3 tens and 5 ones
= 400 + 30 + 5
We write the expanded form of the numbers as
435 = 400 + 30 + 5
Hence, in the number 435, the place value of 4, 3 and 5 are 400, 30 and 5 respectively.
In place value and face value let us first understand the concept of place value of the concerned digits by following the examples.
(i) 350 means: 3 hundreds 5 tens and 0 ones
= 300 + 50 + 0
350 = 300 + 50 + 0
In the number 350, the place value of 3, 5 and 0 are 300, 50 and 0 respectively.
(ii) 602 means: 6 hundreds 0 tens and 2 ones
= 600 + 00 + 2
602 = 600 + 00 + 2
In the number 602, the place value of 6, 0 and 2 are 600, 00 and 2 respectively.
(iii) 278 means: 2 hundreds 7 tens and 8 ones
= 200 + 70 + 8
278 = 200 + 70 + 8
In the number 278, the place value of 2, 7 and 8 are 200, 70 and 8 respectively.
(iv) 777 means: 7 hundreds 7 tens and 7 ones
= 700 + 70 + 7
777 = 700 + 70 + 7
In the number 777, the place value of 7, 7 and 7 are 700, 70 and 7 respectively.
(v) 63 means: 0 hundreds 6 tens and 3 ones
= 000 + 60 + 3
63 = 000 + 60 + 3
In the number 63, the place value of 0, 6 and 3 are 000, 60 and 3 respectively.
Therefore, the place value of a digit in a number is the value of the place which it has in the number.
In the number 549, the place value of 5 is 500, of 4 is 40 and 9 is 9 as 5 occupies the place of hundreds, 4 occupies the place of tens and 9 occupies the place of ones or unit in the given number 549.
We know the digit in a number occupy the place of ones, tens, hundreds, thousands, etc. from extreme right to left and have the value of that place.
The original value of a digit is called its face value.
In the number 385;
the place value of 3 is 300 and its face value is 3,
the place value of 8 is 80 and its face value is 8,
the place value of 5 is 5 and its face value is 5.
Therefore, in any number its important to know the place value and face value of a concerned digit.
Place Value and Face Value of a Number Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
Worksheet on Place Value and Face Value
Questions and Answers on Place Value and Face Value:
1. Fill in the blanks. One has been done for you.
(i) 1 ten = 10 ones
(ii) 2 tens = __________
(iii) 3 tens = __________
(iv) 4 tens = __________
(v) 5 tens = __________
(vi) 6 tens = __________
(vii) 7 tens = __________
(viii) 8 tens = __________
(ix) 9 tens = __________
Word Problem on Face Value Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
2. Write the place value of all the digits in the following numbers.
|
|
Number |
Face Value |
Place Value |
3. Write the place value of the coloured digits. One has been done for you.
|
(i) |
725 |
2 tens or 20 |
|
(ii) |
425 |
_______________ |
|
(iii) |
806 |
_______________ |
|
(iv) |
219 |
_______________ |
|
(v) |
423 |
_______________ |
|
(vi) |
990 |
_______________ |
|
(vii) |
341 |
_______________ |
|
(viii) |
889 |
_______________ |
Word Problems on Combination of Place Value and Face Value Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
4. Write the face value of each digit in the numeral 785:
(i) Face value of 7 = _____
(i) Face value of 8 = _____
(i) Face value of 5 = _____
You might like these
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students.
Cardinal Numbers and Ordinal Numbers | Cardinal Numbers | Ordinal Num
Cardinal numbers and ordinal numbers are explained here with the help of colorful pictures. There are many steps in a staircase as shown in the above figure. The given staircase has nine steps,
Worksheet on Cardinal Numbers and Ordinal Numbers | Cardinal & Ordinal
Worksheet on cardinal numbers and ordinal numbers, activities are given below so that kids can practice. This sheet will help the children to write the numbers in both cardinal and ordinal.
Worksheet on Two Digit Numbers | Numbers in Words | Two-Digit Numbers
In worksheet on 2-digit numbers we will write the number which come before, after and in between, write the numerals, write the number names, place value and face value of 2-digit numbers, numbers in expanded form, write the numbers in short form, write the tens and the ones
Comparison of Two-digit Numbers | Arrange 2-digit Numbers | Examples
What are the rules for the comparison of two-digit numbers? We know that a two-digit number is always greater than a single digit number. But, when both the numbers are two-digit numbers
Adding 1-Digit Number | Understand the Concept one Digit Number |Video
Understand the concept of adding 1-digit number with the help of objects as well as numbers.
Adding 2-Digit Numbers | Add Two Two-Digit Numbers without Carrying
Here we will learn adding 2-digit numbers without regrouping and start working with easy numbers to get acquainted with the addition of two numbers.
Subtracting 1-Digit Number | Subtract Two One-Digit Number | Video
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction means to take away a set of objects from a collection.
Addition Word Problems – 2-Digit Numbers | Addition Word Problems
Basic concept on addition word problems – 2-digit numbers without regrouping for 2nd graders. Students need to read the questions carefully and find the sums of these 2-digit by 2-digit
Subtraction Word Problems - 2-Digit Numbers | Subtraction Problems
Understand the concept on subtraction word problems - 2-digit numbers for the second grade. Read the question carefully to subtract the two-digit numbers to find the differences and follow the
Adding 2-Digit Numbers with Regrouping Video | Add 2 Two-Digit Numbers
Here we will learn adding 2-digit numbers with regrouping and start working with easy numbers to get acquainted with the addition of two numbers.
Subtracting 2-Digit Numbers Video | How to Subtract Two Digit Numbers?
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from
Greater than and Less than Symbols | Rules to Compare the Numbers
To learn greater than and less than symbols its important to recall that every number on a number ray is greater than each number on its left and less than each number on its right.
Names of Three Digit Numbers | Place Value |2- Digit Numbers|Worksheet
How to write the names of three digit numbers? (i) The name of one-digit numbers are according to the names of the digits 1 (one), 2 (two), 3 (three), 4 (four), 5 (five), 6 (six), 7 (seven)
Worksheet on Three-digit Numbers | Write the Missing Numbers | Pattern
Practice the questions given in worksheet on three-digit numbers. The questions are based on writing the missing number in the correct order, patterns, 3-digit number in words, number names in figures, place value and numbers in expand form.
From Place Value and Face Value to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 17, 25 01:54 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 17, 25 01:17 PM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
Apr 17, 25 12:21 PM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Math Place Value | Place Value | Place Value Chart | Ones and Tens
Apr 16, 25 03:10 PM
0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are one-digit numbers. Numbers from 10 to 99 are two-digit numbers. Let us look at the digit 6 in the number 64. It is in the tens place of the number. 6 tens = 60 So… -
Place Value and Face Value | Place and Face Value of Larger Number
Apr 16, 25 02:55 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th…
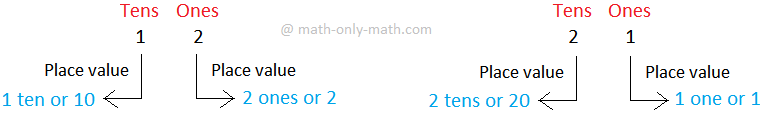
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.