Comparison of Two-digit Numbers

What are the rules for the comparison of two-digit numbers?

We know that a two-digit number is always greater than a single digit number. But, when both the numbers are two-digit numbers, then we must consider the following facts:

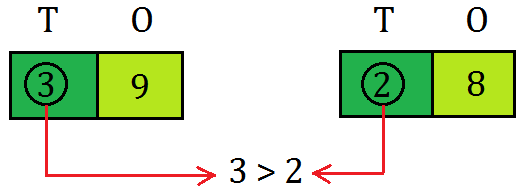
(i) The number having greater valued digit at ten’s place is greater as:

79 > 69,  78 > 65,  53 > 49,  etc.

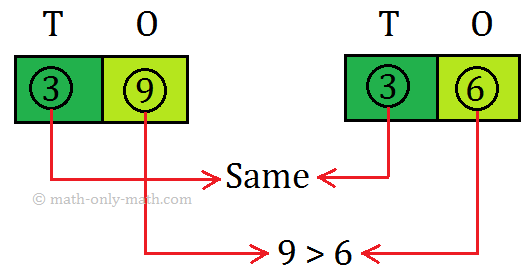
(ii) If the digits at ten’s place of both the numbers are equal, then the digits at one’s place of both the numbers are considered. The number having the greater digit at one’s place is greater than the other.

As:

59 > 56,  47 > 43,  38 > 31,  etc.

Comparison of Two-digit Numbers Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

Comparing Numbers:

We can compare two or more numbers based on the place value of the digits.

Case I: Different Number of Digits

Every 2-digit number is greater than any 1-digit number.

For Example: Which number is greater 48 or 9?

In both of these numbers, we compare the number of digits.

     T     O          T     O 

     4     8                 9

48 has more number of digits than 9.

So, 48 > 9 or 9 < 48.

Remember:

> means greater than

< means smaller than

= means equal to

Case II: Same Number of Digits

If both the numbers have 2 digits, then a number with a greater digit at the tens place is greater than a number with a smaller digit at the tens place.

For Example: Which number is greater 41 or 14?

In both of these numbers, we compare the digits at tens place.

We see,

4 tens > 1 ten

So, 41 > 14.

If both 2-digit numbers have same digits at the tens place, then the number with a greater digit at ones place is greater.

For Example: Which number is greater 68 or 63?

First, we compare the digits at tens place.

Both numbers have same digit at tens place.

Now, comparing the digits at ones place,

we see, 8 ones > 3 ones.

So, 68 > 63

How to arrange 2-digit numbers in ascending and descending order:

(i) Arranging the numbers 37, 15, 71, 46, 29 in ascending order:

The numbers are arranged in ascending order 15, 29, 37, 46, 71.

(ii) Arranging the numbers 24, 18, 32, 55, 96 in descending order:

The numbers are arranged in descending order 96, 55, 32, 24, 18.

(iii) Arranging the numbers 47, 25, 11, 63, 39 in ascending order: The numbers are arranged in ascending order 11, 25, 39, 47, 63.

(iv) Arranging the numbers 74, 98, 22, 51, 61 in descending order:

The numbers are arranged in descending order 98, 74, 61, 51, 22.

Thus, any three-digit number is always greater than a two-digit number.

100 > 99 , 130 > 70 , 150 > 50 , etc.

Solved Examples on Comparison of 2-Digit Numbers:

1. Compare 39 and 28.

Solution:

Compare the digits at the tens place first.

The number with the greater digit at the tens place is greater.

So, 39 > 28.

Remember: 

A 2-digit number is always greater than a 1-digit number.

2. Compare 39 and 36.

Solution:

If the digits at the tens place are same, compare the digits at the ones place.

So, 39 > 36.

3rd Grade Math Lessons

From Comparison of Two-digit Numbers to HOME PAGE