Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Facts about Subtraction
The operation to finding the difference between two numbers is called subtraction. Let us know some facts about subtraction which will help us to learn subtraction of large numbers.
We know that subtraction is taking something away from a group of things. The terms used in subtraction are Minus, Less, Difference, Decrease, Take Away, Deduct. While finding the difference, we write the greater of the two given numbers on the top and them subtract.
When we have to find the difference between two or more numbers we use subtraction.
The sign of subtraction is –.
A number subtracted from itself give zero. i.e.,
8 – 8 = 0
55 – 55 = 0
99 – 99 = 0
Zero subtracted from any number gives the number itself. E.g.,
7 – 0 = 7
46 – 0 = 46
95 – 0 = 95
1. Subtraction with small numbers can be worked out horizontally.
Example: 8 – 5 = 3
24 – 4 = 20
2. Subtraction with large numbers is worked out vertically. Numbers are written under the place value chart.
Example: Th H T O
8 6 7 2
- 5 4 3 2
3 2 4 0
3. Zero subtracted from a number does not change the value of the number.
Example: H T O
2 5 8
+ 0
2 5 8
4. 1 subtracted from a number gives the predecessor of the number as the difference.
Example:
5. The number from which the other number is to be subtracted is called the minuend. The number subtracted is called the subtrahend and the answer is called the difference.
Example:
6. If the subtrahend is missing, then the difference is subtracted from the minuend.
Minuend – difference = subtrahend.
Example:
Workings:
7. To find the missing minuend, the difference is added to the subtrahend.
Difference + subtrahend = minuend
Example:
Workings:
Note: Here in workings we did difference + subtrahend = minuend
Subtraction Facts:
If from seven things we take away four things, then three things are arithmetic this is written in a short way as follows:-
7 - 4 = 3
The sign is called the minus sign and shows that the number written after it is to be subtracted, or taken away, from the number written before it
We may read 7 - 4 = 3 as 'seven minus four is equal to three' or 'seven less four is three'.
Example:
A man had 6 goats. He sold 2 of them. How many had he left?
We know that when 2 things are taken from 6 things there are then 4 things left. Therefore the answer to the question is 4 goats.
This subtraction sum may be written down in either of the following ways:
|
6 - 2 = 4 or |
6 - 2 4 |
You will notice that to subtract 2 from 6 is the same as finding what must be added to 2 to make 6. This is a good way of doing subtraction sums. Thus, in subtracting 2 from 6 you say in your mind '2 and how many more make 6?'
The answer is 4.
SUMMARY of Facts about Subtraction:
👉 The answer to a subtraction sum is called the difference.
👉 When we subtract zero from any number we get the number itself.
👉 When we subtract a number from itself, we get zero always.
👉 We can check subtraction by suitable addition.
👉We solve problems involving both addition and subtraction step by step. First we add and then subtract.
Questions and Answers on Facts about Subtraction:
I. Subtract the following –
(i) 8 – 8 = _____
(ii) 6 – 6 = _____
(iii) 5 – 0 = _____
(iv) 3 – 0 = _____
(v) 9 – 3 = _____
(vi) 8 – 3 = _____
(vii) 7 – 1 = _____
(viii) 47 – 47 = _____
(ix) 59 – 59 = _____
(x) 34 – 0 = _____
(xi) 90 – 0 = _____
(xii) 85 – 44 = _____
(xiii) 32 – 21 = _____
(xiv) 65 – 33 = _____
Answer:
I. (i) 0
(ii) 0
(iii) 5
(iv) 3
(v) 6
(vi) 5
(vii) 6
(viii) 0
(ix) 0
(x) 34
(xi) 90
(xii) 41
(xiii) 11
(xiv) 32
II. Subtract the following –
(i) 9 – 9 = _____
(ii) 2 – 2 = _____
(iii) 7 – 0 = _____
(iv) 5 – 0 = _____
(v) 8 – 3 = _____
(vi) 9 – 4 = _____
(vii) 2 – 1 = _____
(viii) 6 – 1 = _____
(ix) 11 – 11 = _____
(x) 36 – 36 = _____
(xi) 72 – 0 = _____
(xii) 22 – 0 = _____
(xiii) 58 – 28 = _____
(xiv) 46 – 23 = _____
(xv) 86 - 35 = _____
(xvi) 78 – 16 = _____
Answer:
II. (i) 0
(ii) 0
(iii) 7
(iv) 5
(v) 5
(vi) 5
(vii) 1
(viii) 5
(ix) 0
(x) 0
(xi) 72
(xii) 22
(xiii) 30
(xiv) 23
(xv) 51
(xvi) 62
III. Solve the following:
(i) 63 – 20 =
(ii) 89 – 53 =
(iii) 50 – 29 =
(iv) 35 – 0 =
(v) 95 – 48 =
(vi) 22 – 8 =
(vii) 53 – 46 =
(viii) 72 – 36 =
(ix) 63 – 20 =
(x) 29 – 29 =
(xi) 72 – 25 =
(xii) 79 – 29 =
(xiii) 52 – 33 =
(xiv) 93 – 49 =
(xv) 76 – 56 =
Answer:
III. (i) 43
(ii) 36
(iii) 21
(iv) 35
(v) 47
(vi) 14
(vii) 7
(viii) 36
(ix) 43
(x) 0
(xi) 47
(xii) 50
(xiii) 19
(xiv) 44
(xv) 20
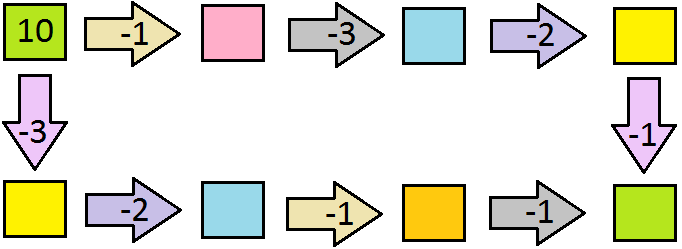
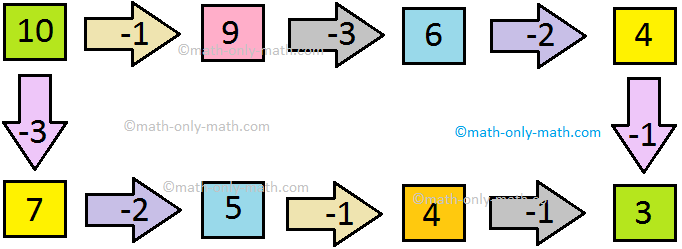
IV. Solve the puzzle. Subtract to fill the empty boxes:
Answer:
IV.
9, 6, 4 and 5, 4, 3
From Facts about Subtraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

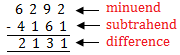




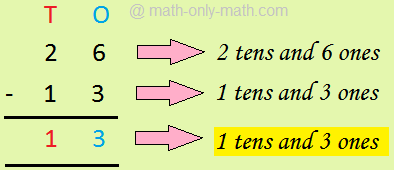
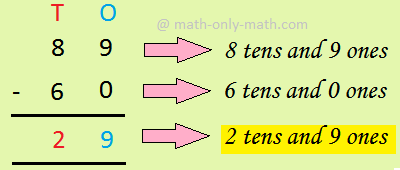


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.