Estimating a Sum

We will learn the basic knowledge for estimating a sum. Here we will learn an easy way to estimate a sum of two numbers by rounding.

In case of two digit numbers we can only round the number to the nearest tens place i.e. only one place estimate.

For example, let us estimate the following sums:

(i) 47 + 32

We need to round the number to the nearest 10.

47 → 50

32 → 30

50 + 30 = 80

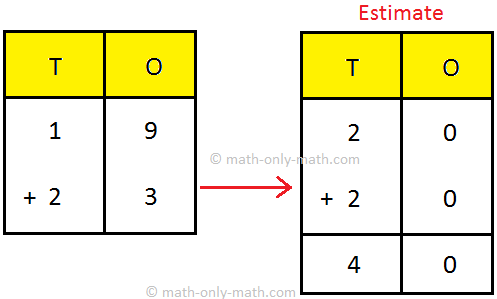
(ii) 25 + 34

We need to round the number to the nearest 10.

25 → 30

34 → 30

30 + 30 = 60

(iii) 75 + 13

We need to round the number to the nearest 10.

75 → 80

13 → 10

80 + 10 = 90

To estimate the sum we round-off each number to the nearest tens and then add the rounded-off numbers.

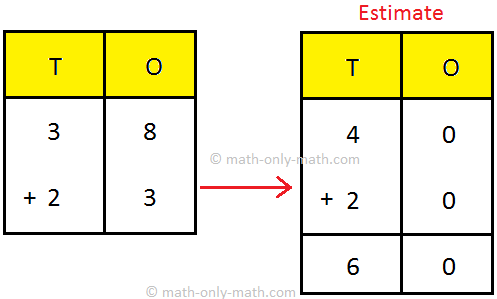
Let us estimate 38 + 23.

38 is nearer to 40 than 30.

So, 38 is rounded up to 40.

The number 23 is nearer to 20 than 30.

So, 23 is rounded down to 20.

Solved Examples on Estimating the Sum:

1. Estimate the sums of 72 and 48

Solution:

We round the number to the nearest 10.

72 → 70

48 → 50

So, 72 is nearest to 70 and 48 is nearest to 50

70 + 50 = 120

Thus the estimated sum = 120

2. Estimate the sums to the nearest ten and also find the actual sum of 87 and 79.

Solution:

We round the number to the nearest 10.

87 → 90

79 → 80

So, 87 is nearest to 90 and 79 is nearest to 80

90 + 80 = 170

Thus the estimated sum = 170

The actual sum of 87 and 79

87 + 79 = 166

Thus the actual sum = 166

Note: To estimate to the nearest 10, we see the digit/number at one’s place. It is converted to 0 or 10 as proper. If the digit/number is < 10/2, it is converted to zero and if it is > 10/2, it is converted to 10.

Estimating the Sum of 3-Digit Numbers:

In case of three digit numbers we can only round the number to the nearest tens place i.e. only one place estimate.

For example, let us estimate the following sums:

1. Estimate the sums of 586 and 120

Solution:

We round the number to the nearest hundred.

586 → 600

120 → 100

So, 586 is nearest to hundred is 600 and 120 is nearest to hundred 100

600 + 100 = 700

Thus the estimated sum to nearest hundred = 700

We round the number to the nearest tens.

586 → 590

120 → 120

So, 586 is nearest to ten is 590 and 120 is nearest to hundred 120

590 + 120 = 710

Thus the estimated sum to nearest ten = 710

We have learnt rounding off numbers. We can use the rounding off to estimate the sum of two numbers. Rounding off to the nearest ten will result in the estimated answer to be closest to the actual one.

2. Estimate the sum of 415 and 214 to the nearest 10's.

Solution:

Rounding off the numbers to the nearest 10's, we get

415   →   420

214   →   210

Now, 420 + 210 = 630

Thus, the estimated sum is 630.

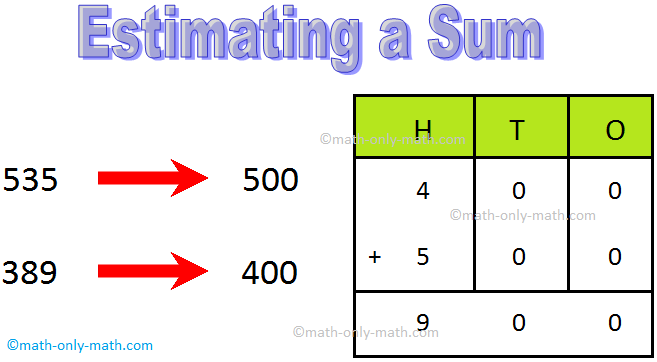
3. Round off the numbers 389 and 535 to the nearest 100s. Find the estimated and the actual sum.

Solution:

Rounding off the numbers to nearest 100s

Hence, 400 + 500 = 900 is the estimated sum.

4. Estimate the sum of 1235 and 1695 to the nearest 100's.

Solution:

Rounding off the numbers to the nearest 100's, we get

1235     →     1200

1695     →     1700

Now, 1200 + 1700 = 2900

Thus, the estimated sum is 2900.

In general, 

When we add two 2-digit numbers we begin adding from the ones place.

For estimating the sum of two 2-digit numbers, just add the tens place and add ten more. The actual answer may be a little more or a little less, but the difference will never be more than 10. That is a fair estimate.

5. Estimate the sum of 34 and 22.

Solution:

Thus, we say that the sum of 34 and 22 is about 60.

6. There are 45 mangoes and 28 oranges in a bag. About how many fruits are there in the bag?

Worksheet on Estimating a Sum:

I. Estimate the sum. One has been done for you.

(i) 19 + 23

(ii) 27 + 44

(iii) 54 + 36

(iv) 41 + 38

(v) 52 + 17

(vi) 26 + 28

Answer:

I. (ii) 30 + 40 = 70

(iii) 50 + 40 = 90

(iv) 40 + 40 = 80

(v) 50 + 20 = 70

(vi) 30 + 30 = 60

II. Round off the given numbers to the nearest 100s. Find the estimated and the actual sum.

Answer:

II. (i) 800, 739

(ii) 400, 408

(iii) 900, 923

(iv) 500, 543

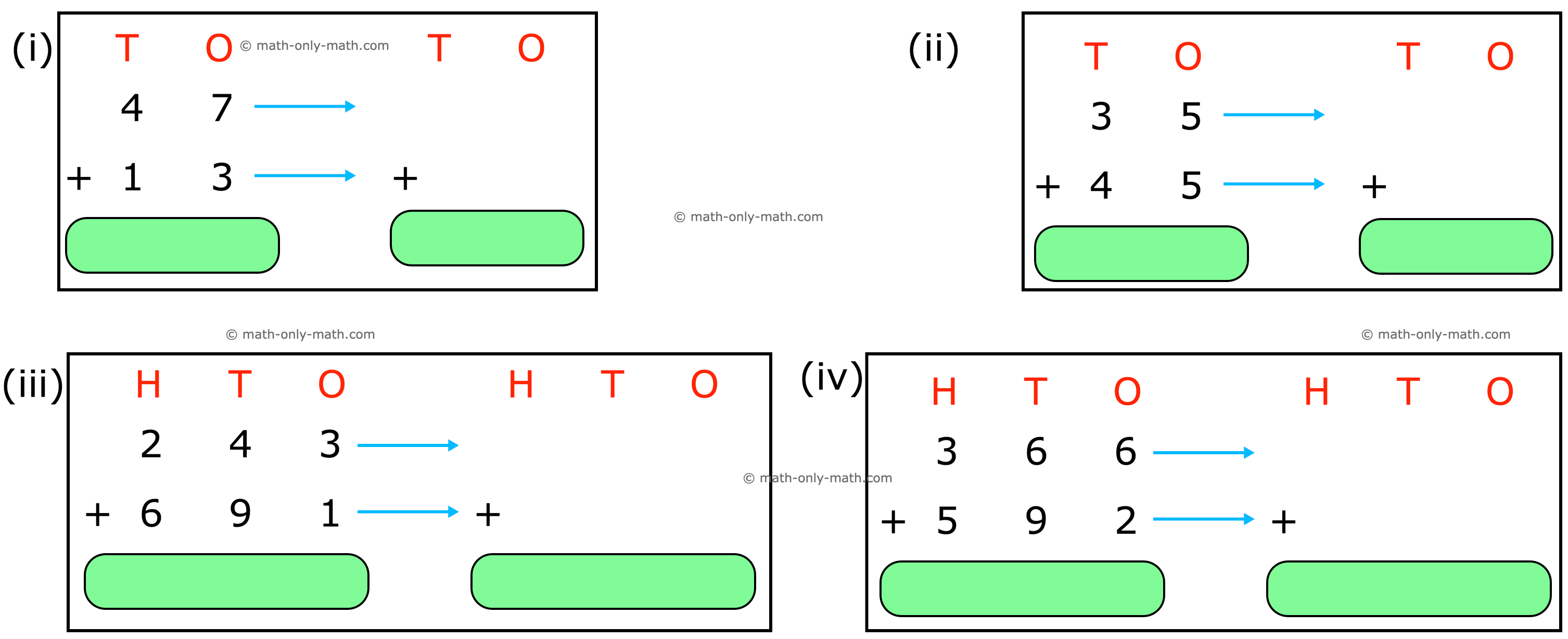
III. First find the actual sum and then estimated sum:

Answer:

III. (i) 60; 60

(ii) 80; 90

(iii) 934; 930

(iv) 958; 960

IV. Estimate the sum to the nearest 10's by first rounding off the numbers:

(i) 348 + 472

(ii) 2651 + 1279

(iii) 1295 + 2365

Answer:

IV. (i) 820

(ii) 3930

(iii) 3670

3rd Grade Math Lessons

From Estimating a Sum to HOE PAGE