Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Face Value and Place Value
Each digit of a number has a place value and a face value.
The place value of each digit in a number depends upon its place in the number.
The face value of a digit is the same as the digit itself, regardless of its position in the number.
Let us understand it by taking some examples.
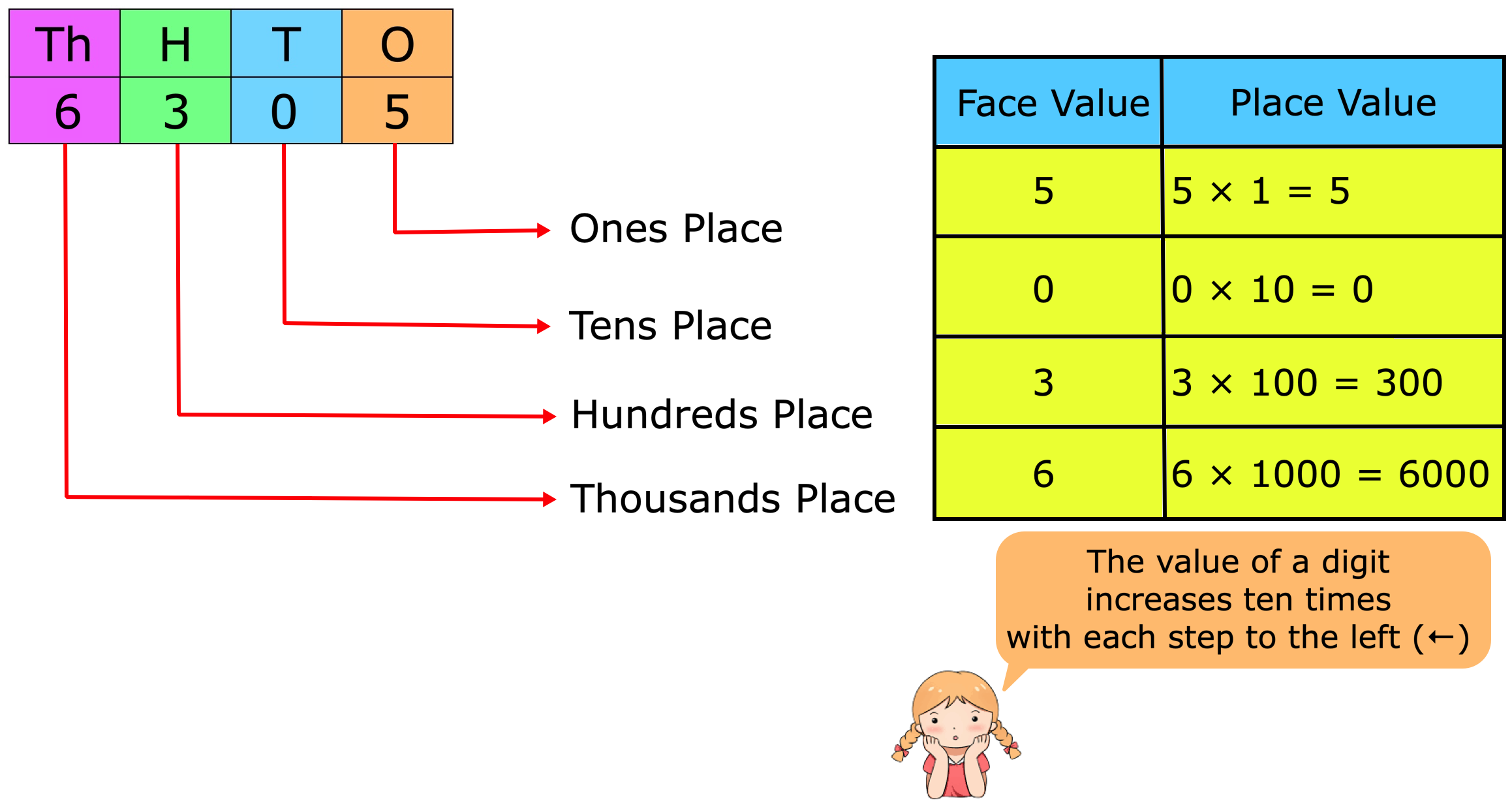
1. Find the place value of all the digits in 7462.
Example:
1. Find the place value of all the digits in 7462.
Solution:
Place Value of a Number Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is the difference between face value and place value of digits?
Before we proceed to face value and place value let us recall the expanded form of a number.
The expanded form of 534 is 500 + 30 + 4
We read it as five hundred thirty four.
Similarly, 798 = 700 + 90 + 8
We read it as seven hundred ninety eight.
2936 = 2000 + 900 + 30 + 6 = Two thousand nine hundred thirty six
For example similarly, all numbers can be written in
expanded form and read accordingly.
(i) 35 = 30 + 5 = Thirty five
(ii) 327 = 300 + 20 + 7 = Three hundred twenty seven
(iii) 942 = 900 + 40 + 2 = Nine hundred forty two
(iv) 1246 = 1000 + 200 + 40 + 6 = One thousand two hundred forty six
(v) 3584 = 3000 + 500 + 80 + 4 = Three thousand five hundred eighty four
(vi) 5167 = 5000 + 100 + 60 + 7 = Five thousand one hundred sixty seven
The digits of a number express the values of their own when the number is given in expanded form and read in words. The value of a digit when expressed in expanded form of the number is called its place value in the number.
For example:
(i) In the number 378;
the place value of 3 is 300 (three hundred)
the place value of 7 is 70 (seventy)
the place value of 8 is 8 (eight)
(ii) In the number 5269;
the place value of 5 is 5000 (five thousand)
the place value of 2 is 200 (two hundred)
the place value of 6 is 60 (sixty)
the place value of 9 is 9 (nine)
Thus, the place value of a digit in a number is the value it holds to be at the place in the number. If 5 is at Thousand-place in a number, its place value will be 5000, if it is at Hundred-place, its value will be 500, etc.
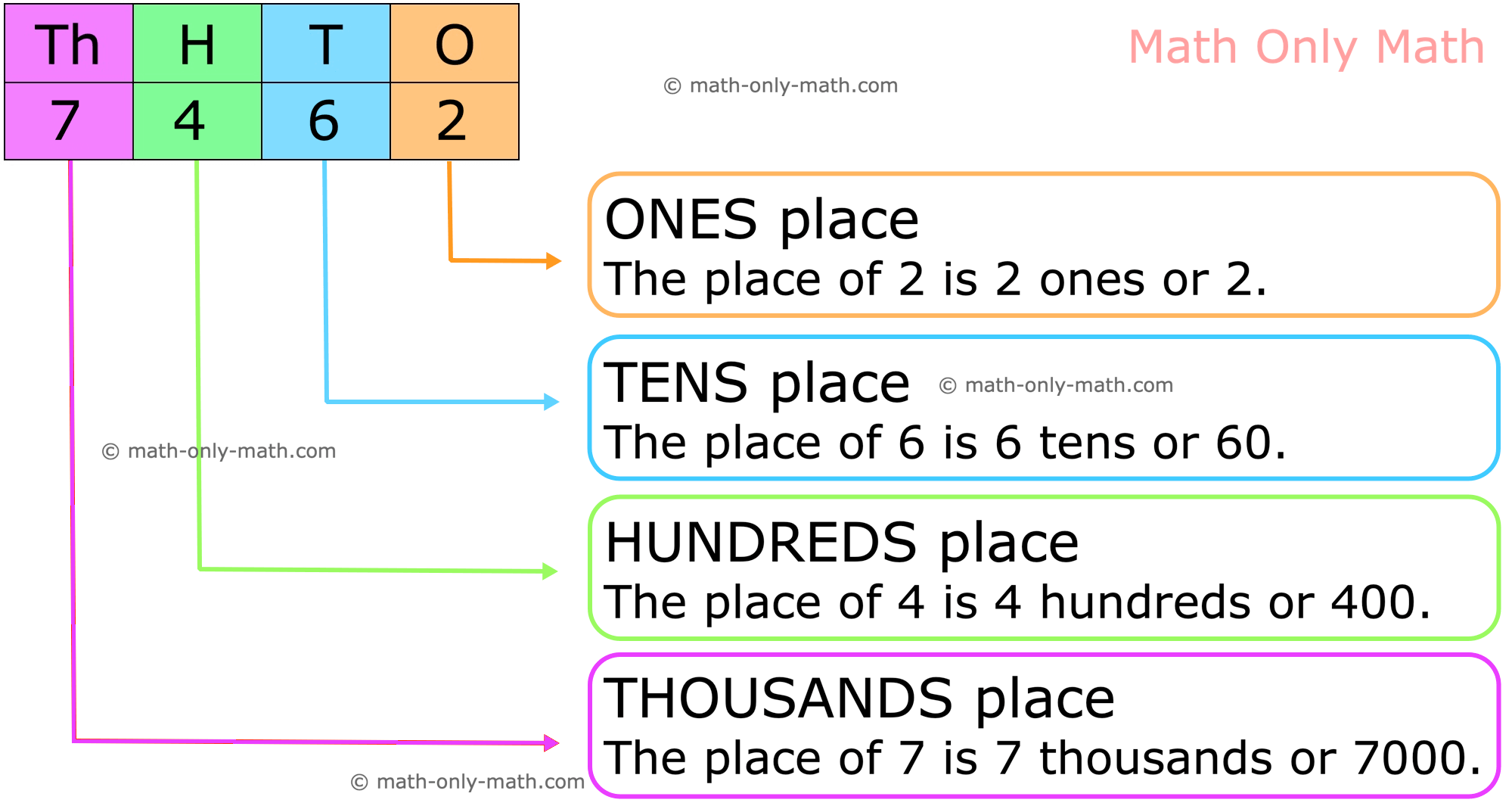
In the number 2137, 2 is at Thousand-place, 1 is at Hundred-place, 3 is at ten’s-place and 7 is at one’s-place. So, the place values of the digits 2, 1, 3 and 7 are 2000, 100, 30 and 7.
Place Value of a Digit = Digit × Position of digit
For example,
(i) Place value of 7 in 3765 is 7 × 100 = 700 or 7 Hundreds.
(ii) Place value of 9 in 9210 is 9 × 1000 = 9000 or 9 Thousands.
(iii) Place value of 4 in 5642 is 4 × 10 = 40 or 4 Tens.
Now, let us find place value of each digit of the numbers given below.
(i) 5672; (ii) 4198
(i) 5672
In the number 5672
The place value of 5 is 5000 (in words five thousand)
The place value of 6 is 600 (in words six hundred)
The place value of 7 is 70 (in words seventy)
The place value of 2 is 2 (in words two)
(ii) 4198
In the number 4198
The place value of 4 is 4000 (in words four thousand)
The place value of 1 is 100 (in words one hundred)
The place value of 9 is 90 (in words ninety)
The place value of 8 is 8 (in words eight)
We know that the face value of a digit is the digit itself, at whatever place it may be. The face value of a digit never changes. It is unchangeable and definite. But place value changes according to the digit’s place.
The face value of digit 9 is 9.
The face value of digit 1 is 1.
The face value of digit 5 is 5.
For example; to find face value and place value of 3572:
face value of 2 is 2 place value of 2 is 2
face value of 7 is 7 place value of 7 is 70
face value of 5 is 5 place value of 5 is 500
face value of 3 is 3 place value of 3 is 3000
The face value as well as place value of zero (0) is always (0).
Face Value of a Number Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
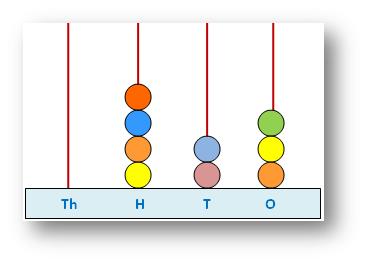
We used the spike-abacus to show, to read and to write a number properly. Now with our knowledge of the values of the digits we read and write the numbers without the help of an abacus.
This abacus shows the number 423.
|
According to the abacus, 4 beads are at H-place (hundred-place) 2 beads are at T-place (ten’s place) 3 beads are at one’s place Hence, the number = 400 + 20 + 3 = 423 |
Now, having the knowledge of face value and place value of the digit, we ascertain the total value of a number; as:
In 423;
the face value of 4 is 4 and place value of 4 is 400
the face value of 2 is 2 and place value of 2 is 20
the face value of 3 is 3 and place value of 3 is 3
So, 423 = 400 + 20 + 3
It is read as, four hundred, twenty and three or four hundred twenty three.
The face value of a digit is the digit itself. Face value of a digit is unchangeable and definite. But place value changes according to the digit’s place.
For example, face value of 5 in 3547 is 5 and in 8599 is also 5.
Similarly, face value of 7 in 2736 is 7.
Now, let us find the face value and place value of all the digits in number 9283.
Face value 3 is 3 and place value of 3 is 3.
Face value 8 is 8 and place value of 8 is 80.
Face value 2 is 2 and place value of 2 is 200.
Face value 9 is 9 and place value of 9 is 9000
Note: Place value and face value of 0 is always 0.
Till now we have learnt that every digit has a place value as well as face value. Face value of a number does not change whereas place value changes according to the position of the digit in a numeral.
For example, in 32753281, the digit 7 is at one lakhs place.
So, its place value is given by 7 × 100000 i.e., 700000.
Of course, its face value is 7.
Place Value = Face Value × Value of the place.
Place Value and Face Value of a Number Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Worksheet on Place Vale and Face Value:
I. Write the place value and face value of each underlined digit:
|
Se (i) (ii) (iii) (iv) (v) (vi) (vii) |
Number 3807 4915 6003 1273 6835 2084 3910 |
Place value __________ __________ __________ __________ __________ __________ __________ |
Face Value __________ __________ __________ __________ __________ __________ __________ |
Answer:
I. (i) 800, 8
(ii) 4000, 4
(iii) 3, 3
(iv) 200, 2
(v) 30, 3
(vi) 2000, 2
(vii) 10, 1
Word Problem on Face Value Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
II. Write the face value and place value of the digits given in red. One has been done for you.
|
Number |
Face Value |
Place Value | |
|
(i) |
697 |
7 |
7 |
|
(ii) |
321 |
_____ |
_____ |
|
(iii) |
816 |
_____ |
_____ |
|
(iv) |
696 |
_____ |
_____ |
|
(v) |
920 |
_____ |
_____ |
Answer:
II. (ii) 3, 300
(iii) 1, 10
(iv) 6, 600
(v) 0, 0
III. Write the missing place value in the blank space:
(i) 5174 = 5000 + 100 + 70 + ………..
(ii) 6797 = 6000 + ……….. + 90 + 7
(iii) 1132 = ……….. + 100 + 30 + 2
(iv) 9679 = ……….. + 600 + 70 + 90
(v) 5864 = 5000 + 800 + 60 + ………..
Answer:
III. (i) 4
(ii) 700
(iii) 1000
(iv) 9000
(v) 4
IV. Write the place value of each colored digit in the following numbers:
(i) 2347
(ii) 6439
(iii) 4685
(iv) 3341
(v) 5519
(vi) 8971
(vii) 8131
(viii) 1112
(ix) 8308
(x) 2101
(xi) 2434
(xii) 6245
Answer:
IV. (i) 300
(ii) 9
(iii) 4000
(iv) 1
(v) 9
(vi) 8000
(vii) 30
(viii) 1000
(ix) 8
(x) 100
(xi) 2000
(xii) 40
Word Problems on Combination of Place Value and Face Value Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
V. Write the place and its face value of the digits given in pink. One has been done for you.
|
Number |
Place |
Face Value | |
|
(i) |
385 |
Tens |
8 |
|
(ii) |
229 |
_____ |
_____ |
|
(iii) |
626 |
_____ |
_____ |
|
(iv) |
926 |
_____ |
_____ |
|
(v) |
706 |
_____ |
_____ |
Answer:
(ii) Ones, 9
(iii) Hundreds, 6
(iv) Hundreds, 9
(v) Tens, 0
Mental maths on Face Value and Place Value
I am a special number.
👉 l am a four-digit number.
👉 My thousands and tens digits are odd.
👉 My hundreds digit is even.
👉 My ones digit is neither even nor odd.
👉 My thousands digit is the biggest 1 digit odd number and my tens digit is smallest odd number.
👉 My hundreds digit is the biggest 1-digit even number.
Can you guess who am I? __________.
Solution:
According to the problem,
Thousands digit is biggest 1 digit odd number ➠ 9
Hundreds digit is biggest 1 digit even number ➠ 8
Tens digit is smallest odd number ➠ 1
Ones digit is neither even nor odd ➠ 0
Therefore, the required special 4-digit number is 9810.
From Face Value and Place Value to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
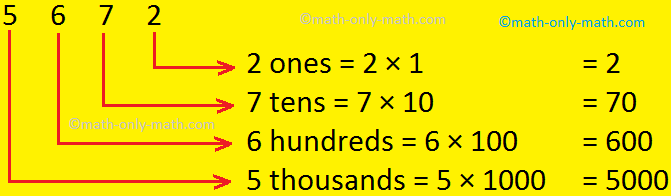
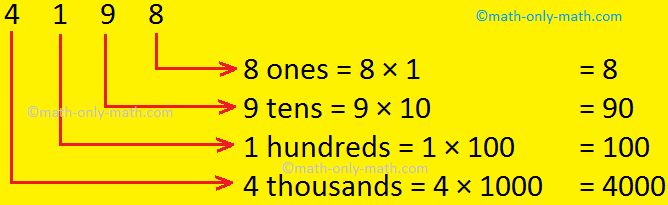


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.