Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Facts about Division
We have already learned division by repeated subtraction, equal sharing/distribution and by short division method. Now, we will read some facts about division to learn long division.
I: Dividing a Number by 0:
1. If the dividend is ‘zero’ then any number as a divisor will give the quotient as ‘zero’.
For example: If ‘zero’ sweets are to be distributed among 8 children, naturally no one will get any sweets.
II: Dividing a Number by 1:
2. If the divisor is ‘1’ then any dividend will have the quotient equal to itself.
How many match sticks in the group?
Obviously, there are 10 match sticks in the group.
We can write this as 10 ÷ 1 = 10.
When we divide a number by 1, the quotient is the number itself.
For example: 4 ÷ 1 = 4
15 ÷ 1 = 15
50 ÷ 1 = 50
For example: There are 15 sweets; each child is to get 1 sweet. How many children get the sweets?

III: Dividing a Number by Itself:
3. When we divide 0 by a number, the quotient is always 0.
How many match sticks in each group?
We can see that there is 1 match stick in every group.
We can write this as
10 ÷ 10 = 1
When we divide a number by itself, the quotient is always 1.
For example: 4 ÷ 4 = 1
15 ÷ 15 = 1
50 ÷ 50 = 1
IV: Dividing 0 by a Number:
4. When we divide 0 by a number, the quotient is always 0.
For example: 0 ÷ 4 = 0
0 ÷ 15 = 0
0 ÷ 50 = 0
5. The product of the divisor and the quotient added to the remainder is always equal to the dividend.
(Divisor × Quotient) + Remainder = Dividend.
(d × q) + r = D
Note: Always find the product first and then add the remainder. (This helps us to check whether the division is done correct or not.)
Example: Divide 23 by 7
Checking:
(d × q) + r = D
(7 × 3) + 2 = 23
21 + 2 = 23
23 = 23
So, the division is correct.
6. In a division sum the remainder is always smaller than the divisor.
Example:
In the last example clearly we can see that the remainder (2) is less than the divisor (7).
7. Every divisor fact has two multiplication facts to verify it.
Example:
In division, 12 ÷ 6 = 2, two multiplication facts are 2 × 6 = 12 and 6 × 2 = 12.
8. The quotient and the divisor are always the factors of the dividend, if there is no remainder.
Example:
|
D 18 3 |
÷ × |
d 3 6 |
= = |
q 6 18 |
9. The dividend is always a multiple of the quotient and divisor, if there is no remainder.
Example:
|
D 30 5 6 |
÷ × × |
d 5 6 5 |
= = = |
q 6 30 30 |
Let us have a quick review of what we have
learnt about division. Division is splitting into equal parts or groups. It is
the result of “fair sharing”.
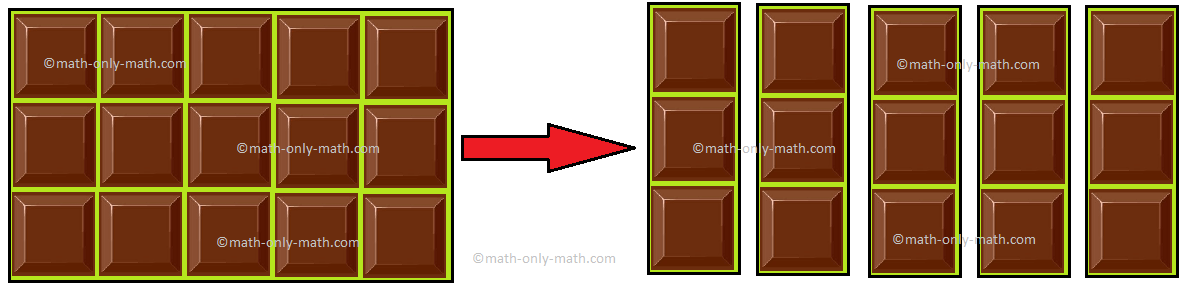
If 5 friends want to share 15 chocolates. How many chocolates will each of them get? Let us divide the chocolates equally amongst them.
15 divided by 5 is 3. They get 3 each.
Division With Remainder
When the given number of things cannot be shared equally something is left over. This is called the remainder.
Example:
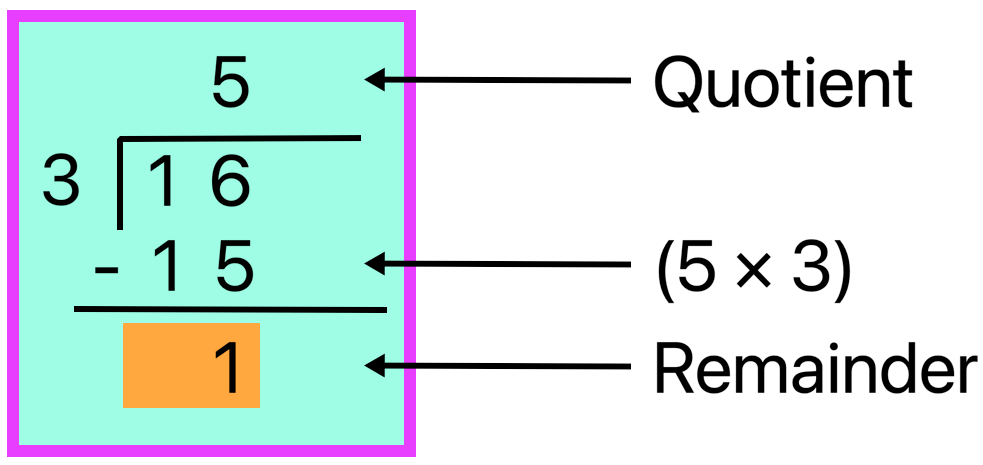
Divide 16 toffees among three children.
Solution:
As 1 is smaller than 3 so we take 16 as dividend
3 × 5 = 15
Write 15 under 16 and subtract
16 - 15 = 1
So, Quotient 5, Remainder = 1
Therefore, each child gets 5 toffees and 1 toffee is left over.
SUMMARY
• In a division sum like 15 ÷ 3 = 5, 15 is called the dividend, 3 is called the divisor and 5 is called the quotient.
• The number which is left undivided in division is called the remainder.
• When 0 is divided by a number, the quotient is 0.
• When a number is divided by 1, the quotient is the number itself.
• Division by 0 has no meaning.
Worksheet on Facts about Division:
1. Fill in the missing numbers:
(i) 5 ÷ 1 = _____
(ii) 0 ÷ 8 = _____
(iii) 17 ÷ _____ =1
(iv) _____ ÷ 1 = 9
(v) _____ ÷ 19 = 0
(vi) 81 ÷ _____ =1
(vii) 14 ÷ _____ =14
(viii) 26 ÷ 26 = _____
(ix) _____ ÷ 99 = 1
Answer:
1. (i) 5
(ii) 0
(iii) 17
(iv) 9
(v) 0
(vi) 81
(vii) 1
(viii) 1
(ix) 99
From Facts about Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

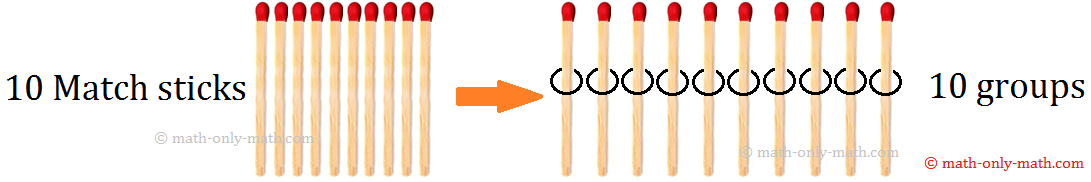
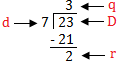


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.