Expanded Form and Short Form of a Number

When we write a number as a sum of place value of its digits, the number is said to be in expended form and when we write a number using digits, the number is said to be in short form.

Expanded Form of a Number:

When we write 3476, the number really means 3000 + 400 + 70 + 6. This means we have expanded the number to show the value of each of its digit.

The expanded form of a number is the method of expressing the number as the sum of the place value of all its digits.

For example,

Consider the number 2815

2815 = 2000 + 800 + 10 + 5

There are 3 ways to write the expanded form for a given number.

Examples on Expanded Form of a Number:

1. Write the expanded form for 43,257.

Solution:

1^st way: 4 ten thousands + 3 thousands + 2 hundreds + 5 tens + 7 ones

2^nd way: 4 × 10000 + 3 × 1000 + 2 × 100 + 5 × 10 + 7 × 1

3^rd way: 40000 + 3000 + 200 + 50 + 7

2. Write the expanded form for 14,080.

Solution:

14,080 = 1 ten thousand + 4 thousands + 8 tens   [Note: We do not write the place value for hundreds and ones as these places are filled with zero.]

or, 1 × 10000 + 4 × 1000 + 8 × 10

or, 10000 + 4000 + 80

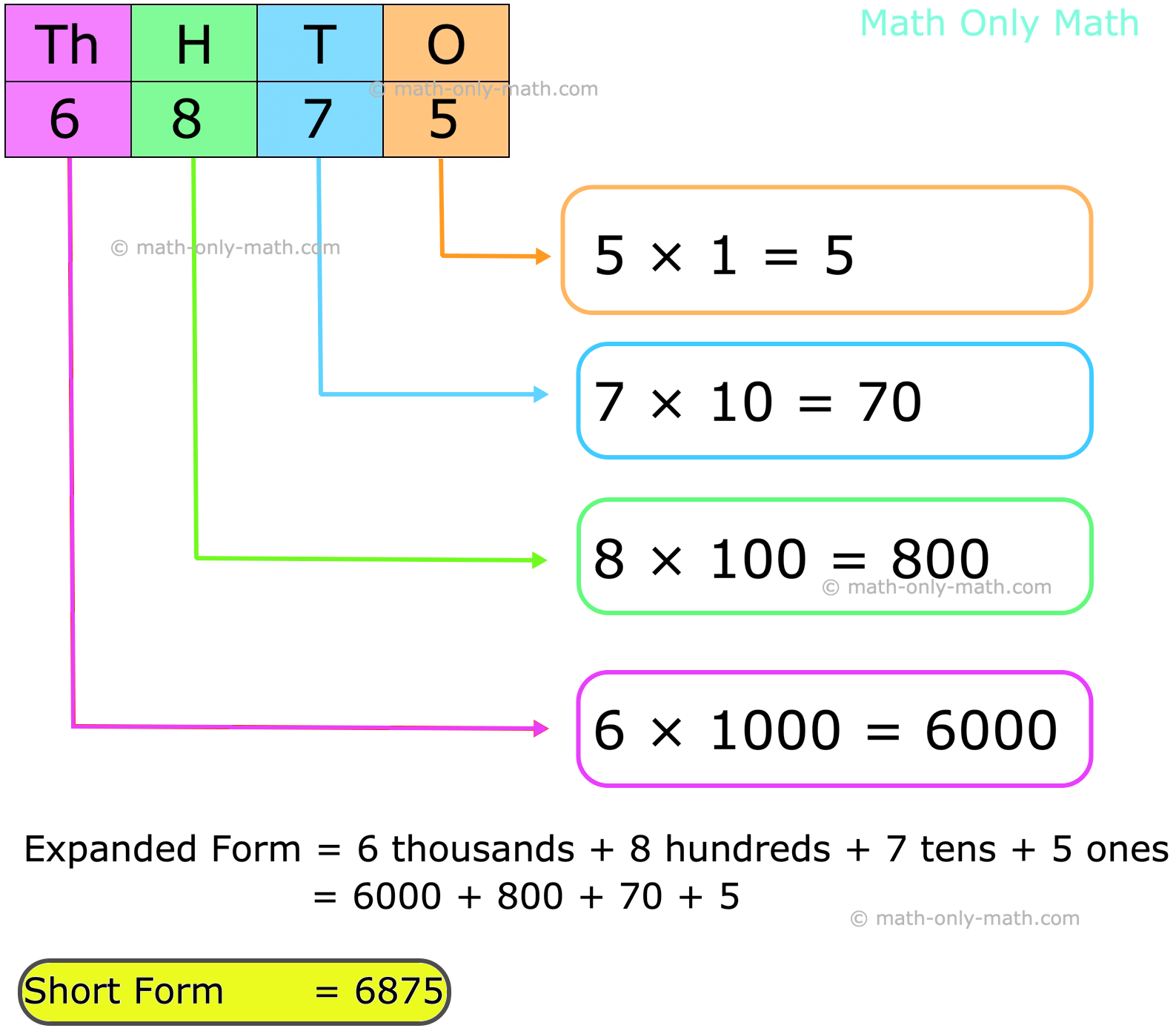
3. Write the expanded form of 6875.

Solution:

Expanded Form = 6 thousands + 8 hundreds + 7 tens + 5 ones

                       = 6000 + 800 + 70 + 5

Standard Form of a Number / Short Form of a Number:

The standard form of a number is a way of expressing the expanded form in figures.

For example, the standard form of 7000 + 400 + 10 + 1 = 7411

Examples on Expanded Form and Short Form of a Number:

3. Write the short form for the given expanded forms.

(i) 8 ten thousands + 6 hundreds + 6 tens + 3 ones

(ii) 9  × 10000 + 7 × 1000 + 4 × 10 + 2

(iii) 40000 + 3000 + 900 + 70 + 8

Solution:

Questions and Answers on Expanded Form and Standard Form of a Number:

I. Write in the expanded form:

(i) 5896

(ii) 3817

(iii) 6399

(iv) 1357

(v) 3434

(vi) 5690

Answer:

I. (i) 5000 + 800 + 90 + 6

(ii) 3000 + 800 + 10 + 7

(iii) 6000 + 300 + 90 + 9

(iv) 1000 + 300 + 50 + 7

(v) 3000 + 400 + 30 + 4

(vi) 5000 + 600 + 90 + 0

II. Write the expanded form:

(i) 4718 = ____ + ___ + __ + _

(ii) 7098 = ____ + ___ + __ + _

(iii) 5002 =  ____ + ___ + __ + _

(iv) 6500 = ____ + ___ + __ + _

(v) 3456 =  ____ + ___ + __ + _

Answer:

II. (i) 4718 = 4000 + 700 + 10 + 8

(ii) 7098 = 7000 + 000 + 90 + 8

(iii) 5002 =  5000 + 000 + 00 + 2

(iv) 6500 = 6000 + 500 + 00 + 0

(v) 3456 =  3000 + 400 + 50 + 6

III. Write in the standard form:

(i) 2000 + 900 + 90 + 9

(ii) 8000 + 200 + 50 + 3

(iii) 1000 + 400 + 50 + 2

(iv) 4000 + 300 + 9

(v) 6000 + 900 + 80 + 4

Answer:

III. (i) 2999

(ii) 8253

(iii) 1452

(iv) 4309

(v) 6984

IV. Write in the short form:

(i) 3000 + 60

(ii) 7000 + 70 + 8

(iii) 8000 + 80 + 9

(iv) 4000 + 500 + 10 + 3

(v) 6000 + 900 + 70

Answer:

IV. Write in the short form:

(i) 3060 

(ii) 7078

(iii) 8089

(iv) 4513

(v) 6970

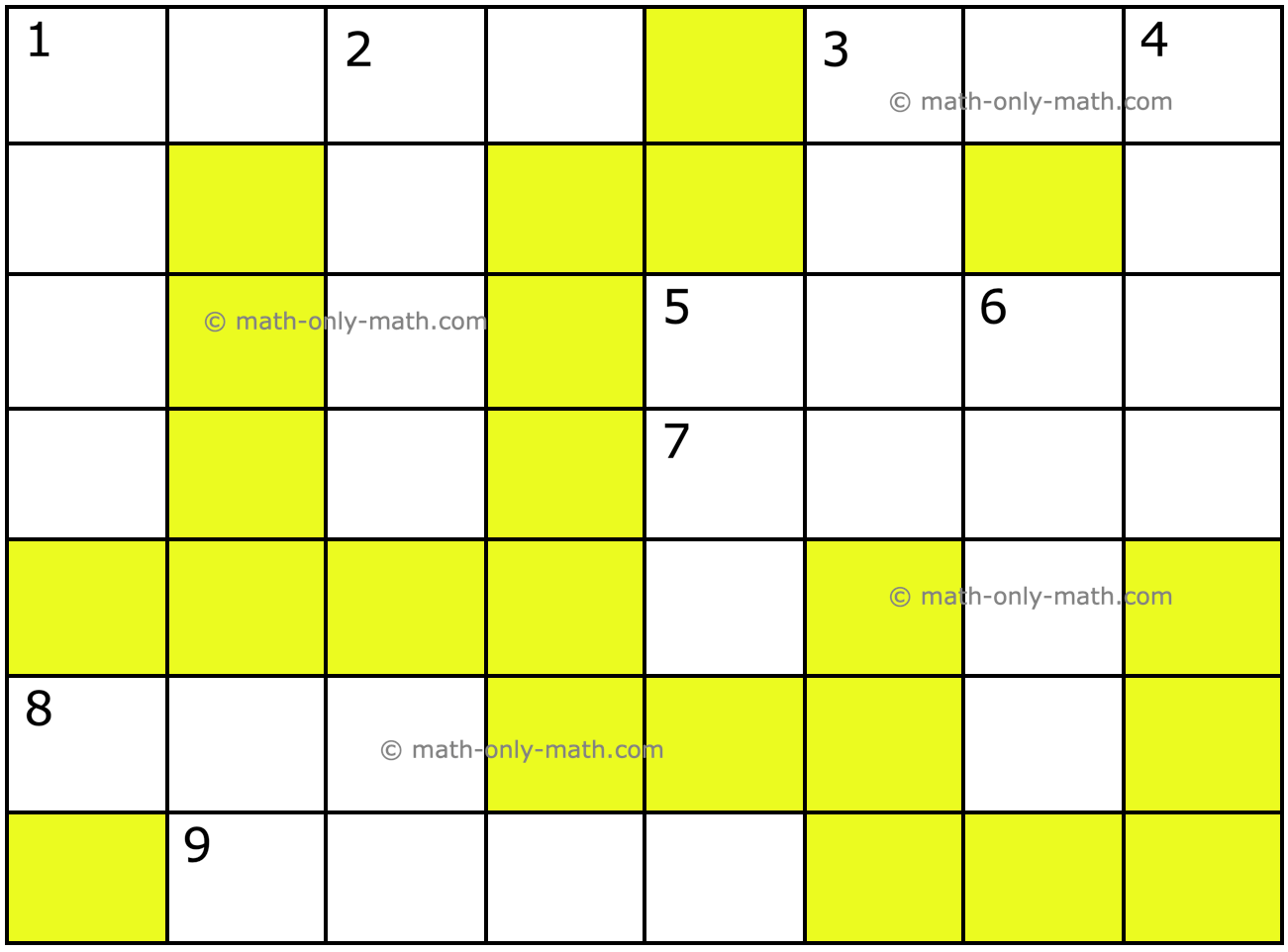
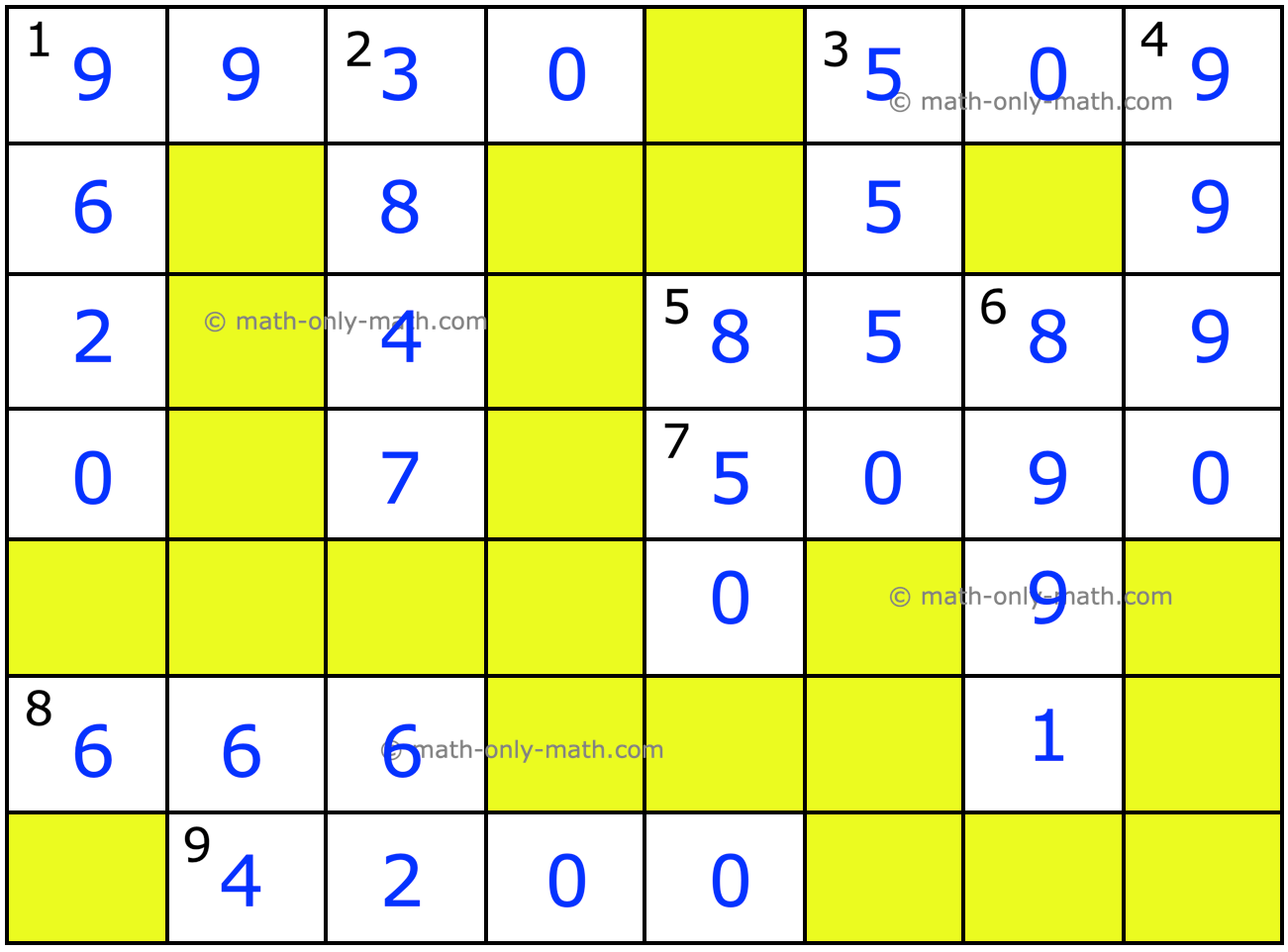
V. Complete the puzzle with answers in short form. Clues have been given below.

Answer:

V. 

Short form of International Number System

VI. Express in short form.

(i) 10,000,000,000 + 2,000,000,000 + 50,000,000 + 5,000,000 +  5,000 + 200 + 40 + 5

(ii) 50,00,00,000 + 3,00,00,000 + 40,00,000 + 5,00,000 + 30,000 + 5,000 + 800 + 50 + 8

(iii) 6,00,00,000 + 20,00,000 + 5,00,000 + 20,,000 + 2000 + 400 + 10 + 2

(iv) 100,000,000,000 + 10,000,000,000 + 2,000,000,000 + 400,000,000,000 + 20,000,000 + 5,000,000 + 100,000 + 20,000 + 4,000 + 300 + 40 + 6

Answer:

VI. (i) 12,555,005,245

(ii) 53,45,35,858

(iii) 6,25,22,412

(iv) 112,425,124,346

3rd Grade Math Lessons

From Expanded Form and Short Form of a Number to HOME PAGE