Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
cos θ = 0
How to find the general solution of the equation cos θ = 0?
Prove that the general solution of cos θ = 0 is θ = (2n + 1)\(\frac{π}{2}\), n ∈ Z
Solution:
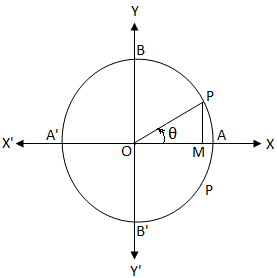
According to the figure, by definition, we have,
Cosine function is defined as the ratio of the side adjacent divided by the hypotenuse.
Let O be the centre of a unit circle. We know that in unit circle, the length of the circumference is 2π.If we started from A and moves in anticlockwise direction then at the points A, B, A', B' and A, the arc length travelled are 0, \(\frac{π}{2}\), π, \(\frac{3π}{2}\), and 2π.
Therefore, from the above unit circle it is clear that
cos θ = \(\frac{OM}{OP}\)
Now, cos θ = 0
⇒ \(\frac{OM}{OP}\) = 0
⇒ OM = 0.
So when will the cosine be equal to zero?
Clearly, if OM = 0 then the final arm OP of the angle θ coincides with OY or OY'.
Similarly, the final arm OP coincides with OY or OY' when θ = \(\frac{π}{2}\), \(\frac{3π}{2}\), \(\frac{5π}{2}\), \(\frac{7π}{2}\), ……….. , -\(\frac{π}{2}\), -\(\frac{3π}{2}\), -\(\frac{5π}{2}\), -\(\frac{7π}{2}\), ……….. i.e. when θ is an odd multiple of \(\frac{π}{2}\) i.e., when θ = (2n + 1)\(\frac{π}{2}\), where n ∈ Z (i.e., n = 0, ± 1, ± 2, ± 3, …….)
Hence, θ = (2n + 1)\(\frac{π}{2}\), n ∈ Z is the general solution of the given equation cos θ = 0
1. Find the general solution of the trigonometric equation cos 3x = 0
Solution:
cos 3x = 0
⇒ 3x = (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. [Since, we know that the general solution of the given equation cos θ = 0 is (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. ]
⇒ x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
Therefore, the general solution of the trigonometric equation cos 3x = 0 is x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
2. Find the general solution of the trigonometric equation cos \(\frac{3x}{2}\) = 0
Solution:
cos 3x = 0
⇒ 3x = (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. [Since, we know that the general solution of the given equation cos θ = 0 is (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. ]
⇒ x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
Therefore, the general solution of the trigonometric equation cos 3x = 0 is x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
3. Find the general solutions of the equation 2 sin\(^{2}\) θ + sin\(^{2}\) 2θ = 2
Solution:
2 sin\(^{2}\) θ + sin\(^{2}\) 2θ = 2
⇒ sin\(^{2}\) 2θ + 2 sin\(^{2}\) θ - 2 = 0
⇒ 4 sin\(^{2}\) θ cos\(^{2}\) θ - 2 (1 - sin\(^{2}\) θ) = 0
⇒ 2 sin\(^{2}\) θ cos\(^{2}\) θ - cos\(^{2}\) θ = 0
⇒ cos\(^{2}\) θ (2 sin\(^{2}\) θ - 1) = 0
⇒ cos\(^{2}\) θ (1 - 2 sin\(^{2}\) θ) = 0
⇒ cos\(^{2}\) θ cos 2θ = 0
⇒ either cos\(^{2}\) θ = 0 or, cos 2θ = 0
⇒ cos θ = 0 or, cos 2θ = 0
⇒ θ = (2n + 1)\(\frac{π}{2}\) or, 2θ = (2n + 1)\(\frac{π}{2}\) i.e., θ = (2n + 1)\(\frac{π}{2}\)
Therefore, the general solutions of the equation 2 sin\(^{2}\) θ + sin\(^{2}\) 2θ = 2 are θ = (2n + 1)\(\frac{π}{2}\) and θ = (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, …….
4. Find the general solution of the trigonometric equation cos\(^{2}\) 3x = 0
Solution:
cos\(^{2}\) 3x = 0
cos 3x = 0
⇒ 3x = (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. [Since, we know that the general solution of the given equation cos θ
= 0 is (2n + 1)\(\frac{π}{2}\), where, n = 0, ± 1, ± 2, ± 3, ……. ]
⇒ x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
Therefore, the general solution of the trigonometric equation cos 3x\(^{2}\) = 0 is x = (2n + 1)\(\frac{π}{6}\), where, n = 0, ± 1, ± 2, ± 3, …….
5. What is the general solution of the trigonometric equation sin\(^{8}\) x + cos\(^{8}\) x = \(\frac{17}{32}\)?
Solution:
⇒ (sin\(^{4}\) x + cos\(^{4}\) x)\(^{2}\) – 2 sin\(^{4}\) x cos\(^{4}\) x = \(\frac{17}{32}\)
⇒ [(sin\(^{2}\) x + cos\(^{2}\) x)\(^{2}\) - 2 sin\(^{2}\) x cos\(^{2}\) x]\(^{2}\) - \(\frac{(2 sinx cosx)^{4}}{8}\) = \(\frac{17}{32}\)
⇒ [1- \(\frac{1}{2}\)sin\(^{2}\) 2x ]2 - \(\frac{1}{8}\)sin\(^{4}\) 2x = \(\frac{17}{32}\)
⇒ 32 [1- sin\(^{2}\) 2x + \(\frac{1}{4}\) sin\(^{4}\) 2x] - 4 sin\(^{4}\) 2x = 17
⇒ 32 - 32 sin\(^{2}\) 2x + 8 sin\(^{4}\) 2x - 4 sin\(^{4}\) 2x – 17 = 0
⇒ 4 sin\(^{4}\) 2x - 32 sin\(^{2}\) 2x + 15 = 0
⇒ 4 sin\(^{4}\) 2x - 2 sin\(^{2}\) 2x – 30 sin\(^{2}\) 2x + 15 = 0
⇒ 2 sin\(^{2}\) 2x (2 sin\(^{2}\) 2x - 1) – 15 (2 sin\(^{2}\) 2x - 1) = 0
⇒ (2 sin\(^{2}\) 2x - 1) (2 sin\(^{2}\) 2x - 15) = 0
Therefore,
either, 2 sin\(^{2}\) 2x - 1 = 0 ……….(1) or, 2 sin\(^{2}\) 2x - 15 = 0 …………(2)
Now, from (1) we get,
1 - 2 sin\(^{2}\) 2x = 0
⇒ cos 4x = 0
⇒ 4x = (2n + 1)\(\frac{π}{2}\), where, n ∈ Z
⇒ x = (2n + 1)\(\frac{π}{8}\), where, n ∈ Z
Again, from (2) we get, 2 sin\(^{2}\) 2x = 15
⇒ sin\(^{2}\) 2x = \(\frac{15}{2}\) which is impossible, since the numerical value of sin 2x cannot be greater than 1.
Therefore, the required general solution is: x = (2n + 1)\(\frac{π}{8}\), where, n ∈ Z
- General solution of the equation sin x = ½
- General solution of the equation cos x = 1/√2
- General solution of the equation tan x = √3
- General Solution of the Equation sin θ = 0
- General Solution of the Equation cos θ = 0
- General Solution of the Equation tan θ = 0
- General Solution of the Equation sin θ = sin ∝
- General Solution of the Equation sin θ = 1
- General Solution of the Equation sin θ = -1
- General Solution of the Equation cos θ = cos ∝
- General Solution of the Equation cos θ = 1
- General Solution of the Equation cos θ = -1
- General Solution of the Equation tan θ = tan ∝
- General Solution of a cos θ + b sin θ = c
- Trigonometric Equation Formula
- Trigonometric Equation using Formula
- General solution of Trigonometric Equation
- Problems on Trigonometric Equation
11 and 12 Grade Math
From cos θ = 0 to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.